
- •Задание 1 Алгоритм построения минимального остовного дерева
- •1.1 Теоретическая часть
- •1.2 Пример выполнения задания
- •1.3 Варианты заданий
- •Задание 2. Алгоритм Дейкстры.
- •2.1 Теоретическая часть
- •2.2 Пример выполнения задания
- •2.3 Варианты заданий
- •Задание 3. Алгоритм Флойда
- •3.1 Теоретическая часть
- •3.2 Пример выполнения задания
- •3.3 Варианты заданий
- •Задание 4 Алгоритм нахождения максимального потока
- •4.1 Теоретическая часть
- •4.2. Пример выполнения задания
- •4.3 Варианты заданий
Задание 1 Алгоритм построения минимального остовного дерева
1.1 Теоретическая часть
Рассмотрим вкратце
алгоритм построения минимального
остовного дерева. Обозначим через
![]() множество узлов сети и введем новые
обозначения:
множество узлов сети и введем новые
обозначения:
![]() — множество узлов
сети, соединенных алгоритмом после
выполнения
— множество узлов
сети, соединенных алгоритмом после
выполнения
![]() -й
итерации этого алгоритма,
-й
итерации этого алгоритма,
![]()
![]() —
множество узлов
сети, не соединенных с узлами множества
—
множество узлов
сети, не соединенных с узлами множества
![]() после выполнения
после выполнения
![]() -й
итерации этого алгоритма.
-й
итерации этого алгоритма.
Этап 0.
Пусть
![]() и
и
![]() .
.
Этап 1.
Выбираем любой узел
![]() из множества
из множества
![]() и определяем
и определяем
![]() ,
тогда
,
тогда
![]() .
Полагаем
.
Полагаем
![]() .
.
Основной этап
![]() .
В множестве
.
В множестве
![]() выбираем узел
выбираем узел
![]() который соединен самой короткой дугой
с каким-либо узлом из множества
который соединен самой короткой дугой
с каким-либо узлом из множества
![]() .
Узел
.
Узел
![]() присоединяется к множеству
присоединяется к множеству
![]() и удаляется из множества
и удаляется из множества
![]() .
Таким образом,
.
Таким образом,
![]() .
Если множество
.
Если множество
![]() пусто, то выполнение алгоритма
заканчивается. В противном случае
полагаем
пусто, то выполнение алгоритма
заканчивается. В противном случае
полагаем
![]() и повторяем последний этап.
и повторяем последний этап.
1.2 Пример выполнения задания
В институте прокладывают компьютерную сеть. В каждом корпусе установлено по одному маршрутизатору. Институт планирует соединить компьютерной сетью шесть корпусов. На рис. 1.1 показана структура планируемой сети и расстояния (в км.) между корпусами. Необходимо спланировать наиболее экономичную компьютерную сеть затратив минимум кабеля.
Этап 0.
Пусть
![]() и
и
![]() .
.
Этап 1.
Выберем узел 1 как начальный узел, внесем
его в множество
![]() и исключим из множества
и исключим из множества
![]() .
Тогда
.
Тогда
![]() .
.
Делаем
![]() .
.

Рисунок 1.1 – Компьютерная сеть института
Этап 2. В
множестве
![]() находим такой узел, который соединен
самой короткой дугой с узлами из множества
находим такой узел, который соединен
самой короткой дугой с узлами из множества
![]() (рис 1.2а). Отыскиваем
(рис 1.2а). Отыскиваем
![]() ,
,
т.к.
![]() .
.
Таким образом
получаем![]() и дугу
и дугу
![]() ,
которую выделяем жирным цветом, т.е.
прокладываем в этом направлении кабель.
Затем исключаем узел 2 из множества
,
которую выделяем жирным цветом, т.е.
прокладываем в этом направлении кабель.
Затем исключаем узел 2 из множества
![]() и добавляем его в множество
и добавляем его в множество
![]() (рис 1.2б). Получаем
(рис 1.2б). Получаем
![]() .
.
Делаем
![]() .
.
Этап 3. В
множестве
![]() находим такой узел, который соединен
самой короткой дугой с узлами из множества
находим такой узел, который соединен
самой короткой дугой с узлами из множества
![]() (рис 1.2б). Ищем
(рис 1.2б). Ищем
![]() ,
,
т.к.
![]() .
.
Таким образом
получаем![]() и дугу
и дугу
![]() ,
по которой прокладываем кабель (рис.
1.2б). Затем исключаем узел 5 из множества
,
по которой прокладываем кабель (рис.
1.2б). Затем исключаем узел 5 из множества
![]() и добавляем его в множество
и добавляем его в множество
![]() .
Получаем
.
Получаем
![]() .
.
Делаем
![]() .
.
Этап 4. В
множестве
![]() находим такой узел, который соединен
самой короткой дугой с узлами из множества
находим такой узел, который соединен
самой короткой дугой с узлами из множества
![]() (рис 1.2в). Находим
(рис 1.2в). Находим
![]() ,
,
т.к.
![]() .
.
Таким образом
получаем![]() и дугу
и дугу
![]() (рис.
1.2в). Затем исключаем узел 4 из множества
(рис.
1.2в). Затем исключаем узел 4 из множества
![]() и добавляем его в множество
и добавляем его в множество
![]() .
Получаем
.
Получаем
![]() .
.
Делаем
![]() .
.
Этап 5. В
множестве
![]() находим такой узел, который соединен
самой короткой дугой с узлами из множества
находим такой узел, который соединен
самой короткой дугой с узлами из множества
![]() (рис 1.2г). Находим
(рис 1.2г). Находим
![]() ,
,
т.к.
![]() .
.
Таким образом
получаем![]() и дугу
и дугу
![]() добавляем к сети (рис. 1.2г). Затем исключаем
узел 6 из множества
добавляем к сети (рис. 1.2г). Затем исключаем
узел 6 из множества
![]() и добавляем его в множество
и добавляем его в множество
![]() .
Получаем
.
Получаем
![]() .
.
Делаем
![]() .
.
Этап 6. В
множестве
![]() находим такой узел, который соединен
самой короткой дугой с узлами из множества
находим такой узел, который соединен
самой короткой дугой с узлами из множества
![]() (рис 1.2д). Находим
(рис 1.2д). Находим
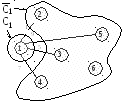
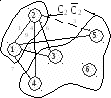
а) Этап 2 б) Этап 3
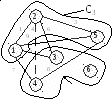
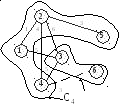
в) Этап 4 г) Этап 5
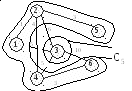

д) Этап 6 е) Этап 7
Рисунок 1.2 – Последовательные итерации выполнения алгоритма построения минимального остовного дерева
![]() ,
,
т.к.
![]() .
.
Таким образом
получаем![]() и из двух подходящих дуг
и из двух подходящих дуг
![]() и
и
![]() выберем одну по желанию, к примеру
выберем
выберем одну по желанию, к примеру
выберем
![]() т.к. у нее меньше номер вершины в множестве
т.к. у нее меньше номер вершины в множестве
![]() .
Добавляем выбранную дугу к сети (рис.
1.2д). Затем исключаем узел 3 из множества
.
Добавляем выбранную дугу к сети (рис.
1.2д). Затем исключаем узел 3 из множества
![]() и добавляем его в множество
и добавляем его в множество
![]() .
Получаем
.
Получаем
![]() .
.
Делаем
![]() .
.
Этап 7. Т.к.
множество
![]() ,
следовательно выполнение алгоритма
закончено. Ответ представлен на рисунке
1.2е. Минимальная длина кабеля для
построения такой сети равна 1+3+4+3+5=16 км.
,
следовательно выполнение алгоритма
закончено. Ответ представлен на рисунке
1.2е. Минимальная длина кабеля для
построения такой сети равна 1+3+4+3+5=16 км.
