Свойства коэффициента эксцесса

• 

• Пусть — независимые случайные величины с равной дисперсией.

Пусть

. Тогда

• Пусть , , 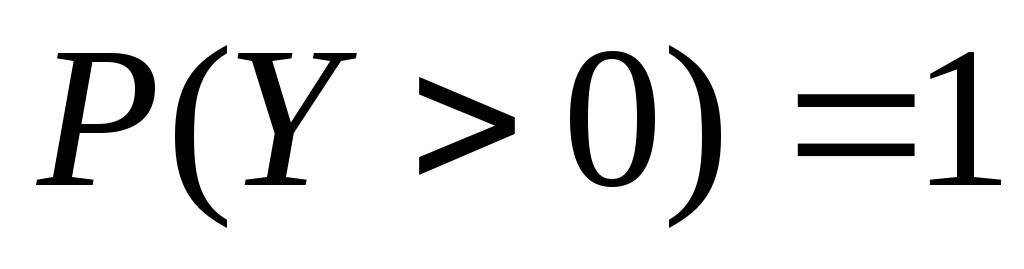; , X,Y – независимы

Тогда æ(XY) >= æ(X), æ(XY) = æ(X)  P(Y=const) = 1

20. Устойчивость нормальных смесей относительно смешивающего распределения: прямая задача.

F(x,y) — смешиваемая функция (нормального распределения) Q(y) — смешивающая

— масштабная смесь

— расстояние

Задача: оценить p( )

Лемма: x₁ ,y₁, x₂, y₂ – независимы, P(Y_i=>0)=1 , то

Сл 1. тогда Сл 2. Сл 3. Пусть хотя бы для одного i тогда p и p Сл 4. Пусть тогда Сл 5. Сл 6. Пусть хотя бы для одного i тогда

21. Устойчивость нормальных смесей относительно смешивающего распределения: обратная задача.

X имеет нормальное распределение.

— характеристическая функция

— производящая функция

— формула обращения

Вывод:

Опр. Метрика Леви  для любого x из R.

Геометрический смысл: максимальная длина стороны квадрата (со сторонами, параллельными осям), который можно вписать между графиками F и G.

22. Моделирование распределений приращений финансовых индексов смесями нормальных законов.

W(x(t)) — процесс моделирующий приращение цен

x(t) — процесс управляет временем

— цена актива

— время заключения j-го контракта

() — процесс изменения цены

T — момент времени

N(T) — число контрактов на время Т

, X_j — независимы

S(T) =

Теорема При некотором имеет место сходимость -> Ф(х)

Пусть при некотором выборе () семейство сл. вел. слабо компактно, тогда

Процесс торгов неоднородный => дважды стохастический (Кокса)

Теорема Пусть X_j — норсв, EX_j=l, DX_j = тогда следующие утверждения эквивалентны:

1) Существует U, т.ч. L(t,l)/tl -> U

2)

3)

4)

Основные виды распределений: