12. Информационные свойства Пуассоновского процесса

Пусть τ[1] … τ[n] – упорядоченные скачки Пуассоновского процесса.

Распределение длин скачков τ[j]–τ[j-1] обладает свойством отсутствия памяти => оно показательно.

Зафиксируем [a; b] на временной оси. Пусть в [a; b] попало n скачков Пуассоновского процесса. Каково их распределение?

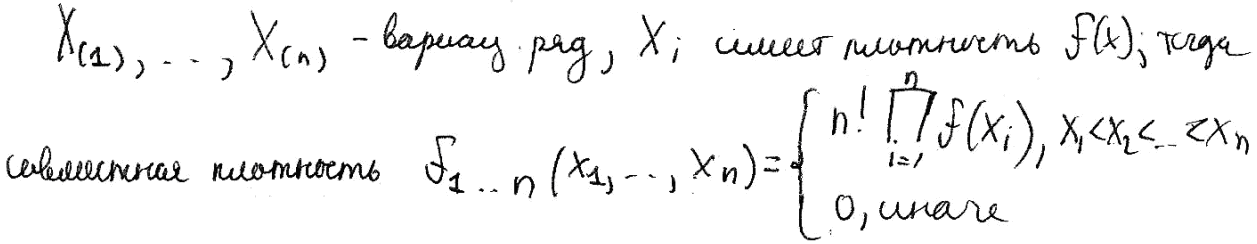
ЦПТ для пуассоновского процесса

Пусть X(t) – пуассоновский процесс.

Теор. => Ф(х), где Ф(х) – функция стандартного распределения N(0,1), причём сходимость равномерна по х, при , т.е.

, С₀ – константа Берри-Эссеена

13. Случайные суммы, их основные свойства; пуассоновские случайные суммы

x₁, x₂, …– н.о.р.с.в., x_i – абсолютно-непрерывная

N – целая неотрицательная случайная величина

x_i, N – определены на одном ВП

Опр.  Случайная сумма S_N = x₁ + x₂ + … + x_N

Свойства:

1. , где

p_n = P(N=n);

F^*n(x) — n-кратная свертка функции распределения F_Xi:

F^*0 — функция распределения с единичным скачком в нуле

2. Если p₀ > 0 => F_SN не является абсолютно непрерывной.

P₀=0 => существует , p^*n(x) n-кратная свертка плотности p_Xi;

3. ; (s) — производящая функция N; f(t) — характ. функция x_i

4. ES_N = EN * EX1; DS_N = DN * (EX₁)² + EN * DX₁

Опр. N ~ П() => S_N есть пуассоновская случайная сумма

Свойства:

1. — характеристическая функция S_N => S_N обладает безгранично делимым распределением.

2. ES_N = EX₁; DS_N =  (EX₁²) ; EN = DN = 

14. Геометрические случайные суммы, теорема Реньи, связь между геометрическими и пуассоновскими случайными суммами

x₁,x₂,.. – н.о.р.с.в.

N ~ Geom (p) =>— геометрическая случайная сумма

; ; _N(s) = ; n=0,1,..

15. Теорема переноса. Аналог теоремы Пуассона для случайных сумм.

Опр.  Схема серий {X_n,j} — последовательность последовательностей н.о.р.с.в. (n фиксировано).

Теорема переноса

Теорема Пуассона для случайных сумм

Вопрос: что и куда переносит теорема переноса?

Ответ: теорема переноса переносит свойства сходимости с сумм неслучайного числа случайных слагаемых на случайные суммы, попутно трансформирую предельный закон.

16.Смеси вероятностных распределений, идентифицируемость, примеры

Опр. Пусть задано вероятностное пространство (Y, , Q) и Q(y) — вероятностная мера.

Тогда — смесь распределения F(x,y) по y относительно Q(y) и F(x,y) — смешиваемая функция, а Q(y) — смешивающая.

При Y(y) = y, H(x) = E F(x, y).

Если существует плотность f(x,y), то — плотность H(x)

Пример

Q — дискретная, принимающая значения (y₁, …) с вероятностями (p₁,…)

_,

— компоненты смеси, — веса компонент

Опр.

— параметр масштаба

— масштабная смесь.

x и (u,v) — стохастически независимы если ,

Опр.  Пусть F(x,y) при любом x,y – ф.р., измеримая по y. Q — семейство случайных величин, — семейство смесей .

Семейство W называется идентифицируемым, если из , где , Q следует .