6. Закон больших чисел

Теорема (ЗБЧ)

Пусть есть бесконечная последовательность норсв , определённых на одном вероятностном пространстве . Пусть .

Обозначим Sn выборочное среднее первых n членов:

Тогда почти наверное.

Оценка скорости сходимости ЗБЧ:

r(n) — скорость сходимости (порядок убывания остатка)

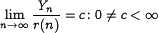
, где — стандартное нормальное распределение.

7. Распределение Пуассона

— распределение Пуассона с параметром λ>0, если X – случайная

величина, принимающая целочисленные неотрицательные значения.

E X = DX = λ

Так что пуассоновское распределение — предельное для биномиального (при ).

Опр.  Схема серий {X_n,j} — последовательность последовательностей н.о.р.с.в. (n фиксировано).

Теорема Пуассона

Пусть в системе серий .

Тогда

Обобщение теоремы Пуассона

Рассматривается та же схема серий.

Пусть , Тогда

8. Устойчивые распределения

Опр. G(x) — устойчивая функция распределения, если для ее характеристической функции g(t) выполнено

или G(a₁*x+b₁)*G(a₂*x+b₂) = G(a*x+b) ( a₁,a₂>0, b₁,b₂ из R, a>0 и b из R)

где * — это свёртка:
а характеристическая функция

Теорема Леви

Пусть X₁, X₂ … — норсв. Тогда F(x) может быть предельной для сумм вида

при некоторых тогда и только тогда, когда F(x) — устойчива.

Опр. Функция распределения F(t) с характеристической функцией f(t) называется безгранично делимой, если характеристическая функция f_n(t) такая, что f(t) = (f_n(t))ⁿ

Теорема Хинчина

Пусть

Тогда F(x) может быть предельной для сумм вида X_n,1 + X_n,2 + … + X_n,mn при  т.и т.т., когда F(x) безгранично делима.

9. Информация и энтропия. Их свойства.

Информация

Опр.  Пусть A – событие, P(A) > 0. Тогда информацией события, содержащейся в А, называется величина

Опр.  Пусть A,B – события, P(A) > 0, P(B) > 0. Тогда информацией события, содержащейся в B относительно А, называется величина

Основание логарифма определяет единицу измерения информации.

Если основание — nat,

если основание 2 — bit.

Основание логарифма всегда больше единицы.

Свойства информации:

1) Чем меньше P(A), тем больше I(A).

2) Если А, В – независимые с.в., I(A|B) = 0.

3) Если А, В – независимые с.в., I(AB) = I(A)+ I(В).

Энтропия

Опр.  Пусть E – эксперимент с исходами и соответствующими им вероятностями

Пусть Q(E) — случайная величина со значениями I(A_i), принимаемыми с вероятностями p.

Тогда энтропией E называется величина

Свойства энтропии:

1)  H(E)0, H(E)=0  p_i=1

2)  Н(Е) не зависит от A, а зависит только от p.

3)  H(E) — непрерывная функция p.

4)  Максимальная энтропия у экспериментов с n исходами у того, у которого исходы равновероятны.

5)  E – эксперимент с исходами

E получается из Е объединением двух исходов с номерами i и j.

E — эксперимент с двумя исходами которым соответствуют вероятности p_i/(p_i+p_j), p_j/(p_i+p_j).

Тогда

Теорема Фадеева

Если функционал H(p₁,..p_n) удовл. 1)-5) =>

10. Дифференциальная энтропия. Свойства некоторых распределений.

Пусть — случайная величина.

•   дискретна. Тогда энтропия равна _,

_{если число значений бесконечно.}

•   абсолютно непрерывна. Тогда энтропия равна

Где f() – плотность распределения . Такая энтропия называется дифференциальной энтропией.

, где R_[-a;a] — равномерное распределение

P() — показательное распределение

N (a, ) — нормальное распределение

Вывод:

1. Равномерное распределение наиболее неопределенное среди всех распределений на конечном отрезке.

2. Показательное распределение наиболее неопределенное среди всех распределений на положительной полуоси.

3. Нормальное распределение наиболее неопределенное среди всех распределений на .

Замечание: на эту теорему может быть задача.

11. Определение пуассоновского процесса.

Опр.  Случайный процесс — семейство случайных величин X(t,), определенное на одном пространстве (), tTR.

Опр.  Траектория случайного процесса — X(t, ) при фиксированном _.

X(t) -> S — множество всех траекторий случайного процесса.

На S можно определить борелевскую сигма-алгебру , порожденную множеством всех открытых подмножеств S.

Событие X(t): -> S — прообраз любого B_.

Опр.  Распределением случайного процесса называется мера P, т.ч. _:

Опр.  Процесс X(t) — процесс с независимым приращением, если

X (t), X (t)-X (t), … , X (t)-X (t) — независимы в совокупности.

Опр.  Процесс X(t) — однородный, если распределение X(t+h) - X(t) совпадает с распределением X(s+h) - X(s) для t, s, h: t, t+h, s, s+h T.

Опр.  Процесс X(t) — пуассоновский, если

1) X(0)=0 почти наверное

2) X(t) имеет независимые приращения

3) X(t) однородный

4) При >0, h>0, h->0

P(X(h) = 0) = 1- h +o(h)

P(X(h) = 1) = h +o(h)

P(X(h) >= 2) = o(h)

– интенсивность пуассоновского процесса.

Для пуассоновского процесса EX(t) = DX(t) = t