1.12. Теоремы Шеннона

При передаче сообщений по каналам связи всегда возникают помехи, приводящие к искажению принимаемых сигналов. Исключение помех при передаче сообщений является очень серьезной теоретической и практической задачей. Ее значимость только возрастает в связи с повсеместным внедрением компьютерных телекоммуникаций. Все естественные человеческие языки обладают большой избыточностью, что позволяет сообщениям, составленным из знаков таких языков, иметь заметную помехоустойчивость.

Избыточность могла бы быть использована и при передаче кодированных сообщений в технических системах. Самый простой способ повышение избыточности — передача текста сообщения несколько раз в одном сеансе связи. Однако большая избыточность приводит к большим временным затратам при передаче информации и требует большого объема памяти. К настоящему времени вопрос об эффективности кодирования изучен достаточно полно.

Пусть задан алфавит , состоящий из конечного числа букв, конечная последовательность символов из называется словом, а множество всех непустых слов в алфавите обозначим через . Аналогично для алфавита слово обозначим , а множество всех непустых слов .

Рассмотрим соответствие между буквами алфавита и словами алфавита : . Это соответствие называется схемой алфавитного кодирования и обозначается . Алфавитное кодирование определяется следующим образом: каждому слову ставится в соответствие слово , называемое кодом слова . Слова называются элементарными кодами. Ограничением задачи передачи кодов является отсутствие помех. Требуется оценить минимальную среднюю длину кодовой комбинации.

При разработке различных систем кодирования данных получены теоретические результаты, позволяющие получить сообщение с минимальной длиной кодов. Два положения из теории эффективности кодирования известны как теоремы Шеннона.

Первая теорема говорит о существовании системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов (букв алфавита ) на единицу сообщения (букву алфавита ) асимптотически стремится к энтропии источника сообщения, т. е. кодирование в пределе не имеет избыточности.

Рассмотрим вновь пример 1 из раздела 1.11, закодировав анализированное сообщение по алгоритму Фано³. В таблице . 1.12 приведены коды букв в сообщении (слова ), длина кода , вероятности букв сообщения , величины и .

Таблица 1.12

Но- мер	Бук- ва	Код
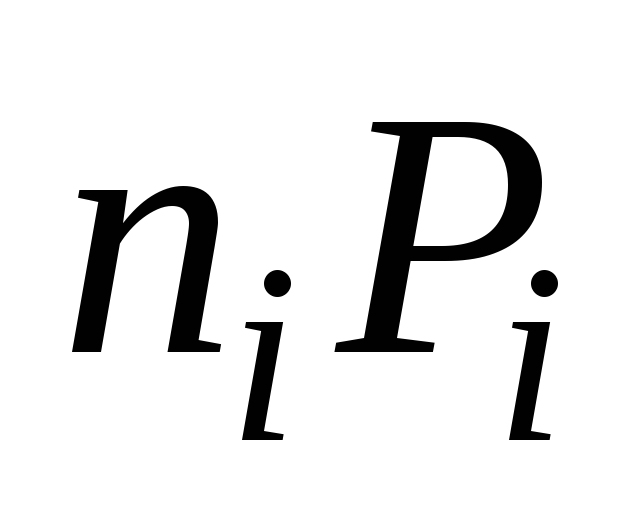
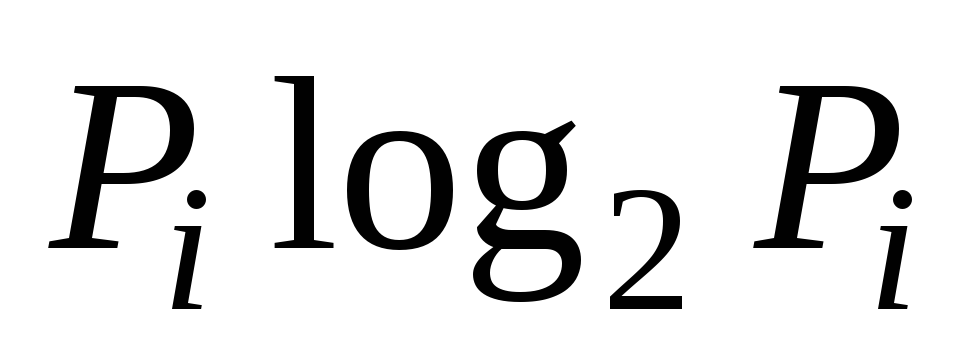
1	ж	10110	5	0.0294	0.1470	–0.1496
2	и	000	3	0.1176	0.3528	–0.3632
3	л	0111	4	0.0883	0.3532	–0.3092
4	-	10111	5	0.0294	0.1470	–0.1496
5	б	0110	4	0.0883	0.3532	–0.3092
6	ы	10101	5	0.0294	0.1470	–0.1496
7	пробел	001	3	0.1176	0.3528	–0.3632
8	а	10100	5	0.0294	0.1470	–0.1496
9	у	1000	4	0.0589	0.2356	–0.2406
10	ш	11000	5	0.0294	0.1470	–0.1496
11	к	010	3	0.1176	0.3528	–0.3632
12	с	11001	5	0.0294	0.1470	–0.1496
13	е	1001	4	0.0589	0.2356	–0.2406
14	р	11010	5	0.0294	0.1470	–0.1496
15	н	11011	5	0.0294	0.1470	–0.1496

Продолжение таблицы 1.12

Но мер	Бук ва	Код
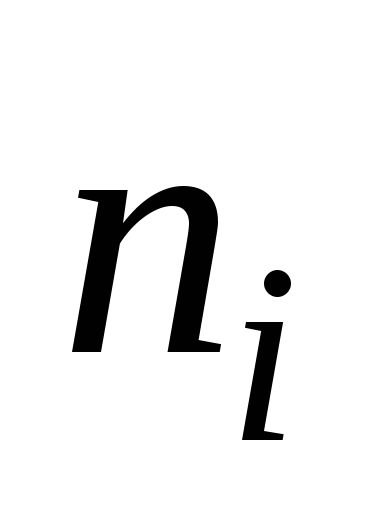
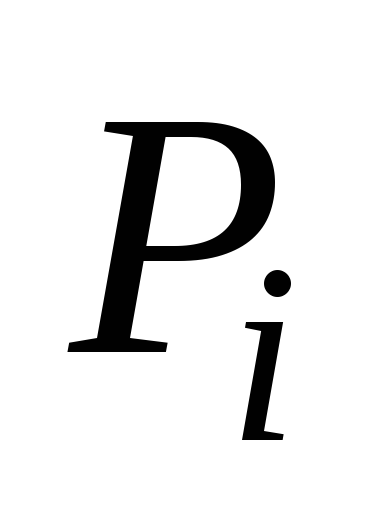
16	ь	11100	5	0.0294	0.1470	–0.1496
17	й	11101	5	0.0294	0.1470	–0.1496
18	о	11110	5	0.0294	0.1470	–0.1496
19	з	11111	5	0.0294	0.1470	–0.1496

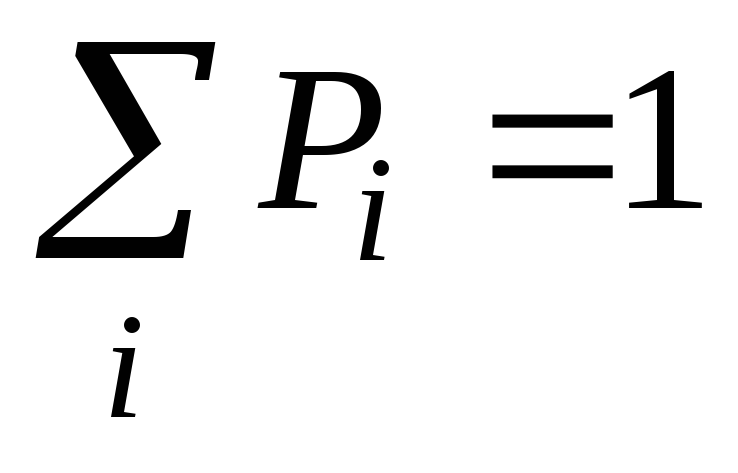
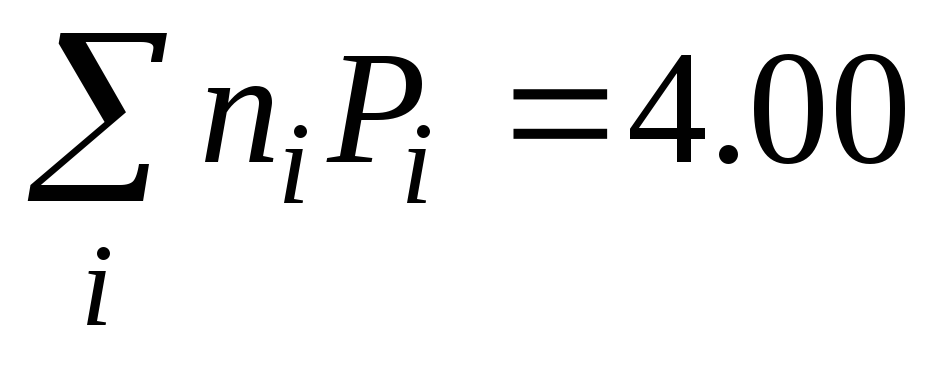
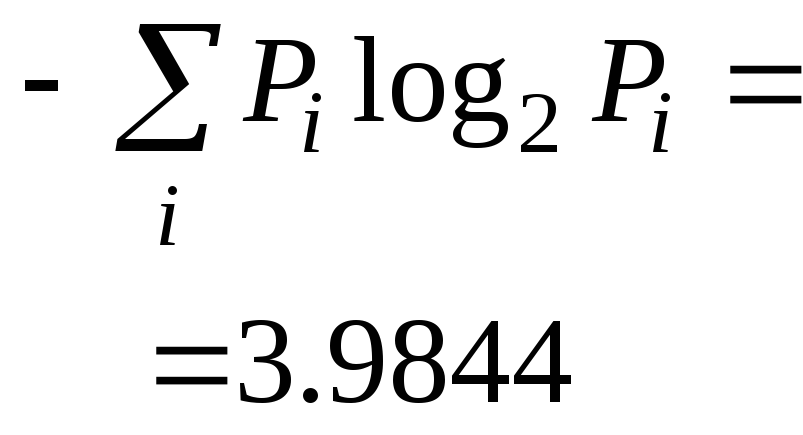
Математическое ожидание количества символов из алфавита при кодировании равно . Этому среднему числу символов соответствует максимальная энтропия . Для обеспечения передачи информации, содержащейся в сообщении, должно выполняться условие . В этом случае закодированное сообщение имеет избыточность. Коэффициент избыточности определяется следующим образом:

, (1.12.1)

. В нашем случае , т. е. код практически не имеет избыточности. Видно, что среднее число двоичных символов стремится к энтропии сообщения.

Вторая теорема Шеннона устанавливает принципы помехоустойчивого кодирования. Оказывается, что даже при наличии помех в канале связи всегда можно найти такую систему кодирования, при которой сообщение будет передано с заданной достоверностью. Основная идея всех таких кодов заключается в следующем: для исправления возможных ошибок вместе с основным сообщением нужно передавать какую-то дополнительную информацию. Для реализации контроля возможных ошибок используются так называемые самокорректирующие коды, а по каналу связи вместе с символами основного сообщения передаются ещё дополнительных символов, обеспечивающих избыточность кодирования и позволяющих противодействовать помехам.