
- •Часть II. Электричество и магнетизм.
- •Цель обучения
- •Содержание лекционного курса «Электричество и магнетизм» Семестр 3
- •Раздел 1. Электростатика /1а, 1б, 2б, 3б, 4б, 6б, 7б/
- •1.1. Предмет классической электродинамики. Электрическое поле. Напряженность электрического поля.
- •1.2. Основные уравнения электростатики в вакууме.
- •1.3. Электростатическое поле в диэлектриках.
- •1.4. Проводники в электростатическом поле. Конденсаторы. Энергия электрического поля.
- •Раздел 2. Постоянный электрический ток /1а, 1б, 2б, 3б, 4б, 6б, 7б/
- •2.1. Постоянный электрический ток.
- •2.2. Основы классической теории электропроводности металлов.
- •2.3. Электрический ток в различных средах.
- •Раздел 3. Магнитное поле постоянного тока. /1а, 1б, 2б, 3б, 4б, 7б, 8б/
- •Раздел 4. Квазистационарные электромагнитные поля. Электромагнитные колебания и волны /2а, 1б, 2б, 3б, 5б, 7б, 8б/
- •4.4. Общие свойства и характеристики волновых процессов.
- •Лекция 1 Предмет классической электродинамики. Электрическое поле. Напряженность электрического поля.
- •1. Электростатика
- •1.1. Электрические заряды. Способы получения зарядов. Закон сохранения электрического заряда.
- •1.2. Взаимодействие электрических зарядов. Закон Кулона. Применение закона Кулона для расчета сил взаимодействия протяженных заряженных тел.
- •1.3. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей.
- •Лекция 2 Основные уравнения электростатики в вакууме.
- •1.4. Поток вектора напряженности электрического поля. Теорема Гаусса.
- •Применение теоремы Гаусса для расчета электрических полей.
- •Работа сил поля по перемещению заряда. Потенциал и разность потенциалов электрического поля.
- •1.7. Связь между напряженностью и потенциалом электрического поля. Градиент потенциала. Теорема о циркуляции электрического поля.
- •1.8. Эквипотенциальные линии и поверхности и их свойства.
- •1.9. Потенциалы простейших электрических полей.
- •Лекция 3 Электростатическое поле в диэлектриках.
- •1.10. Поляризация диэлектриков. Свободные и связанные заряды. Основные виды поляризации диэлектриков.
- •2) Деформационная или электронная поляризация (неполярные диэлектрики).
- •3) Ионная поляризация (кристаллы).
- •4) Сегнетоэлектрики и пироэлектрики.
- •1.11. Вектор поляризации и вектор электрической индукции.
- •1.12. Напряженность электрического поля в диэлектрике.
- •Лекция 4 Проводники в электростатическом поле. Конденсаторы. Энергия электрического поля.
- •1 .15. Равновесное распределение зарядов на проводниках.
- •1.16. Электроемкость проводников. Конденсаторы.
- •1.17. Вычисление емкости простых конденсаторов.
- •1.18. Соединение конденсаторов.
- •1) Последовательное соединение.
- •2) Параллельное соединение.
- •1.19. Энергия системы неподвижных точечных зарядов.
- •1.20. Энергия заряженного проводника и заряженного конденсатора.
- •1.21. Энергия электростатического поля.
- •Лекция 5
- •2. Постоянный электрический ток
- •2.1. Характеристики тока. Сила и плотность тока. Падение потенциала вдоль проводника с током.
- •2.2. Закон Ома для однородного участка цепи. Сопротивление проводников.
- •2.3. Дифференциальная форма закона Ома.
- •2.4. Сторонние силы. Эдс источника тока. Закон Ома для неоднородного участка цепи и для замкнутой цепи.
- •Напряжение на зажимах источника тока.
- •2.6. Разветвленные цепи. Правила Кирхгофа.
- •2.8. Работа и мощность постоянного тока. Закон Джоуля – Ленца.
- •2.9. Кпд источника тока.
- •Лекция 6 Основы классической теории электропроводности металлов.
- •2.10. Природа носителей тока в металлах.
- •2.11. Основные положения классической электронной теории проводимости металлов Друде – Лоренца.
- •2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.
- •2.13. Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов. Открытие высокотемпературной сверхпроводимости.
- •Лекция 7 Электрический ток в различных средах.
- •2.14. Электрический ток в электролитах. Законы электролиза Фарадея.
- •2.15. Электропроводность газов. Основные виды газового разряда. Плазма.
- •2.16. Электрический ток в вакууме. Работа выхода электрона из металла. Явление термоэлектронной эмиссии.
- •Лекция 8
- •3. Магнитостатика
- •Постоянное магнитное поле.
- •3.1. Взаимодействие проводников с током. Закон Ампера.
- •3.2. Закон Био-Савара-Лапласа. Принцип суперпозиции магнитных полей.
- •Лекция 9 Контур с током в магнитном поле.
- •3.4. Магнитный момент тока.
- •3.5. Магнитное поле на оси кругового витка с током.
- •3.6. Момент сил, действующих на контур с током в магнитном поле.
- •3.7. Энергия контура с током в магнитном поле.
- •3.8. Контур с током в неоднородном магнитном поле.
- •3.9. Работа, совершаемая при перемещении контура с током в магнитном поле.
- •Лекция 10 Основные уравнения магнитостатики в вакууме.
- •3.10. Поток вектора магнитной индукции. Теорема Гаусса в магнитостатике. Вихревой характер магнитного поля.
- •3.11. Теорема о циркуляции магнитного поля. Магнитное напряжение.
- •3.12. Магнитное поле соленоида и тороида.
- •1) Магнитное поле на оси прямого длинного соленоида.
- •2) Магнитное поле на оси тороида.
1.18. Соединение конденсаторов.
Соединение конденсаторов бывает последовательным, параллельным и смешанным.
1) Последовательное соединение.
При последовательном соединении заряды на всех конденсаторах одинаковые, а напряжения разные (рис.4.7).
Рис.4.7. Последовательное соединение конденсаторов.

![]()
2) Параллельное соединение.
П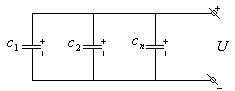 ри
параллельном соединении напряжения на
всех конденсаторах одинаковые
ри
параллельном соединении напряжения на
всех конденсаторах одинаковые
![]() =
U, а заряды – разные
(рис.4.8).
=
U, а заряды – разные
(рис.4.8).
Рис.4.8. Параллельное соединение конденсаторов.
![]()
![]()
1.19. Энергия системы неподвижных точечных зарядов.
Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.
Рис.4.9. К определению энергии системы зарядов.
Рассмотрим сначала систему, состоящую из двух точечных зарядов (рис.4.9). Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q2 к q1 либо q1 к q2. В обоих случаях совершается одинаковая работа:

В последней формуле
последней формуле
![]() - потенциал поля 1-го заряда в том месте,
где находится второй заряд;
- потенциал поля 1-го заряда в том месте,
где находится второй заряд;
![]() - потенциал поля второго заряда в том
месте, где находится первый заряд. С
учетом сказанного, эту формулу можно
записать также в виде:
- потенциал поля второго заряда в том
месте, где находится первый заряд. С
учетом сказанного, эту формулу можно
записать также в виде:
![]() .
.
Рис.4.10. Система трех неподвижных точечных зарядов.
Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов (рис.4.10) может быть представлена в виде:

В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле:
![]()
1.20. Энергия заряженного проводника и заряженного конденсатора.
П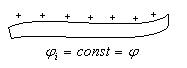 оверхность
заряженного проводника (рис.4.11) при
равновесии зарядов является
эквипотенциальной (φi
= φ = const).
Следовательно, энергия заряженного
проводника:
оверхность
заряженного проводника (рис.4.11) при
равновесии зарядов является
эквипотенциальной (φi
= φ = const).
Следовательно, энергия заряженного
проводника:
![]() ,
где q - заряд проводника.
,
где q - заряд проводника.
Рис.4.11. Заряженный проводник.
![]()

Конденсатор представляет собой пару заряженных проводников (рис.4.12), поэтому имеем:

Рис.4.12. Заряженный конденсатор.
А поскольку заряд
![]() ,
то энергия заряженного конденсатора
может быть представлена одной из трех
формул:
,
то энергия заряженного конденсатора
может быть представлена одной из трех
формул:
![]()
1.21. Энергия электростатического поля.
Выразим энергию заряженного конденсатора через величины, характеризующие электрическое поле, локализованное в пространстве между его обкладками – напряженность поля Е и объем V, занятый полем. Имеем для напряженности поля:
![]() ,
где
,
где
![]() .
.
Воспользовавшись
формулой для емкости плоского конденсатора
![]() ,
находим:
,
находим:
![]()
![]() ,
где
,
где
![]() - объём конденсатора, откуда следует,
что
- объём конденсатора, откуда следует,
что
![]()
Мы видим, что энергия электрического поля прямо пропорциональна квадрату его напряженности Е и объёму V, занятому полем. Величину энергии поля, отнесенной к единице объема, называют плотностью энергии:
![]() - плотность энергии
электрического поля.
- плотность энергии
электрического поля.
