5. Декартово (прямое) произведение множеств

Декартовым произведением двух множеств А и В называют множество всех упорядоченных пар элементов из А и В. Таким образом, АВ={(a,b): аA и bВ}.

Обобщение на систему множеств: пусть {A₁,A₂,A₃,…,A_n} конечная система множеств, тогда A₁  A₂  A₃  … A_n ={(a₁,a₂,…,a_n): a_i  A_i , i=1,2,…,n}. Элементы (a₁,a₂,…,a_n) называются упорядоченными «энками» или кортежами длины n. Если множества A₁,A₂,A₃,…,A_n совпадают и равны A, тогда A₁  A₂  A₃  … A_n  обозначается Aⁿ , если A=ℝ  ℝℝ…ℝ⇋ℝⁿ – называется n‑мерным Евклидовым вещественным пространством, а элементы этого пространства (a₁,a₂,…,a_n) называются n‑мерными векторами или точками.

Примеры:

1) A={a, b, c}; B={0, 1} =>AB={(a,0), (a,1), (b,0), (b,1), (c,0), (c,1)}.

2) A=[-2; 2]; B=[1; 3] => AB={(x,y): -2 x  2,  1 y 3} – прямоугольник на вещественной плоскости.

3) A – круг радиуса r, B=[a, b] – отрезок. Тогда AB – цилиндр радиуса r и высотой (b‑a).

4) A и B – окружности с несовпадающими центрами, тогда AB – поверхность тора.

Множества A и B в прямом произведении АВ называют координатными осями, а элементы xА и yВ – проекциями вектора z=(x,y)АВ на координатные оси или координатами точки z (абсциссой и ординатой соответственно). Будем обозначать их пр_А z и пр_В z.

Пусть множество М АВ, проекцией множества М на ось А называется множество всех абсцисс векторов из М , проекцией множества М на ось В называется множество всех ординат векторов из М, т.о. пр_А М={ пр_А z: zМ}={xА: yВ и (x,y)М} и пр_В М={ пр_В z: zМ}={yВ: xА и (x,y)М}.

Для многомерного случая A₁  A₂   A₃  … A_n , каждое множество A_i называется i-той координатной осью. Проекция вектора z=(a₁, a₂,…, a_n) на i-тую координатную ось равна его i-той координате: пр_i z=a_i , где i=1,2,…,n. Если М A₁  A₂ … A_n , то пр_i М={ пр_i z: zМ}. Определены также проекции вектора z и множества векторов М на несколько координатных осей с номерами i₁, i₂,…,i_k: пр_i1, i2…ik z = ( a_i1, a_i2,…, a_ik) – k‑мерный вектор и пр_i1, i2…ik М = { пр_i1, i2…ik z: zМ } – множество k‑мерных векторов.

Пример:

Т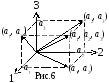ройки вещественных чисел (а₁, а₂, а₃) можно рассматривать как точку в трехмерном пространстве (или вектор, проведенный в эту точку из начала координат). Тогда пр_i (а₁, а₂, а₃)=a_i, где i=1,2,3, пр_i,j (а₁, а₂, а₃)=(a_i, a_j), где i,j=1,2,3. См. рис.6.

6. Некоторые свойства декартова произведения

1) АВВА не коммутативно, действительно, пусть А={a,b}; B={0} AB ={(a,0),(b,0)} и BA={(0,a),(0,b)}.

2) Имеет место дистрибутивность как слева, так и справа к объединению и пересечению: а)  E(A∪B) = (EA) ∪ (EB)  и  (A∪B) E = (AE) ∪ (BE); б)  E(A∩B) = (EA) ∩ (EB)  и  (A∩B)E = (AE) ∩ (BE)

3) (A \ B)  E = (AE) \ (BE)

4) Если AC и BD  AB  CD

5) AB = CD  A=C и B=D

7. Соответствия между множествами

Если элементы множества А некоторым образом сопоставляются элементам множества В, образуя при этом упорядоченные пары связанных элементов, то говорят, что между множествами А и В установлено соответствие, а правило, по которому образуются такие пары, называют законом или графиком соответствия. Или более строго: соответствием между множествами А и В называется тройка множеств Г =(G, A, B), где G  AB = {(x,y): xA, yB} – график соответствия Г или закон соответствия. Множество А – называется областью отправления, а В – областью прибытия соответствия Г.

Если (x,y)  G, то говорят, что элемент y соответствует элементу x при Г или y является образом x относительно G, и обозначают y=G(x); а x называют прообразом y относительно G. Множество всех образов элементов xA называют образом множества А в множестве В и обозначают Г(А)={yB: xA и (x,y)G}. Множество всех прообразов элементов yB называют прообразом множества В в множестве А и обозначают Г^-1(В)={xA: yB и (x,y)G}.

Для всех x из пр_А G={xA: yB и (x,y)G }  A говорят, что соответствие Г определено для x, и множество пр_А G ⇋ пр₁ G называют областью определения Г. Для всех y из пр_В G={yB: xA и (x,y)G}  B, говорят, что y является значением, принимаемым соответствием Г, и множество пр_В G ⇋ пр₂ G называют областью значений Г.

Если пр₁ G = А, то соответствие называют всюду определённым.

Если соответствие всюду определено и при этом пр₂ G = B, то имеет смысл понятие обратного соответствия и обратного графика.

График G^-1, элементами которого являются пары (y,x) такие, что (x,y)G называется обратным к G, т.о. G^-1 = {(y,x): (x,y)  G}. Обратным соответствием к соответствию Г называется Г^‑1 = (G^‑1, B, A).

Понятно, что область определения соответствия Г совпадает с областью значений Г^‑1, а область значений Г совпадает с областью определения Г^‑1, поскольку пр₁ G^-1  B и пр₂ G^-1  A.

Если Г^-1 = Г, то соответствие называется симметричным. При этом выполняется равенство: (Г^‑1)^‑1 = Г.

Пример:

Пусть А={Иван, Жанн, Билл}, В={рус., англ., фр.} и G={(Иван, рус.); (Иван, англ.); (Жанн, фр.); (Жанн, англ.); (Билл, англ.)}. Тогда тройка Г=(G, А, В) задает соответствие между множествами А и В с графиком G (или по закону G). Пусть Х={Иван, Билл}, тогда образом множества Х будет G(X)={рус., англ.}. Если Y={рус., фр.}, то прообразом Y будет множество G^‑1(Y)={Иван, Жанн}. Данное соответствие определено для всех элементов множества А, т.е. область определения пр₁ G = А. Любой элемент множества В является значением соответствия Г, т.е. область значений пр₂ G = B. Обратным соответствием будет соответствие Г^‑1 = (G^‑1, B, A), где G^‑1 ={(рус., Иван); (англ., Иван); (фр., Жанн); (англ., Жанн); (англ., Билл)}. Поскольку Г^-1 Г, соответствие не является симметричным.