11. Фундаментальные циклы и разрезы

Пусть Т – остов графа и К – соответствующий ему ко-лес.

Если добавить к Т любую хорду hК, то получим единственный цикл, который называется фундаментальным циклом относительно хорды h. Понятно, что все циклы, получаемые таким способом, т.е. путем добавления к Т различных хорд из К, попарно различны и их число равно числу хорд в К, и равно (G). Множество всех фундаментальных циклов относительно хорд К называется фундаментальной системой циклов относительно остова Т.

Н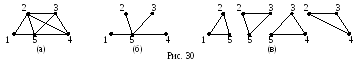 а рисунке 30 (а) и (б) изображен граф и его остов, а на рисунке 30 (в) – фундаментальная система циклов относительно этого остова.

Если удалить из Т любую ветвь b, то одна из компонент Т разобьется на две новые компоненты, каждая из которых является деревом. Обозначим множества вершин новых компонент V₁ и V₂. Заметим теперь, что хорды из К, соединяющие вершины из V₁ и V₂, в совокупности с ветвью b образуют разрез графа G. Этот разрез называется фундаментальным разрезом относительно ветви b остова Т. Множество всех разрезов, полученных таким способом, т.е. удалением по отдельности каждой ветви из Т, называется фундаментальной системой разрезов относительно остова Т. Очевидно, что все разрезы в этом множестве попарно различны и их число совпадает с числом ветвей в Т и равно (в‑k).

Н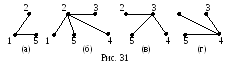а рисунке 31 изображены фундаментальные разрезы графа, изображенного на рис.30(а), относительно его остова на рис.30(б). Рис. 31(а) – фундаментальный разрез относительно ветви (1,5); рис. 31(б) – ф.р. относительно ветви (2,5); рис. 31(в) – ф.р. относительно ветви (3,5) и рис. 31(г) – ф.р. относительно ветви (4,5).

Важной особенностью фундаментальных циклов (разрезов) является то, что любой цикл (разрез) в графе можно представить в виде кольцевой суммы некоторых фундаментальных циклов (разрезов). В этом смысле они образуют базис подпространства всех циклов (разрезов) графа G.

12. Специальные графы

Граф называется r‑валентным или r‑однородным, если любая его вершина имеет степень, равную r.

Например, цикл является 2-валентным графом. На рисунке 32 (а) изображен 3-валентный граф Петерсона, графы Платоновых тел: (б)–куба, (в)‑тетраэдра, (г)–додекаэдра, (д)–4-валентный граф октаэдра и (е)–5-валентный граф икосаэдра.

Л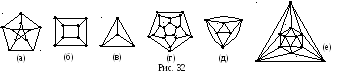 юбой полный граф К_n, где n – число вершин, является (n‑1)‑регулярным.

Граф G=(V, E) называется двудольным, если множество его вершин V можно разбить на два непересекающихся подмножества V₁ и V₂, что каждое ребро графа имеет одну концевую вершину в V₁, а вторую в V₂. См. рис.33 слева. При этом не обязательно, чтобы каждая пара вершин из V₁ и V₂ была соединена ребром. Если же это так, то граф называется полным двудольным графом и обозначается обычно K_m,n, где m и n – число вершин в V₁ и V₂ соответственно. См. рис.33 справа.

В полном двудольном графе число вершин равно m+n, а число ребер mn. Полный двудольный граф вида K_1,n называется звездным.

Граф G=(V, E) называется k‑дольным, если множество его вершин V можно разбить на k попарно непересекающихся подмножеств V₁, V₂,, V_k, что любое ребро имеет одну концевую вершину в V_i, а вторую в V_j, где ij. Полным k‑дольным графом называется такой k‑дольный граф, что любая вершина V_i смежна с любой вершиной из V_j, где ij и i, j=1,2,,k.

Объединение звездного графа K_1,n‑1 и цикла C_n‑1 называется колесом и обозначается W_n.