Рівняння коливання мембрани.
Означення.
Мембраною називається пружна натягнута
плівка, яка вільно прогинається. Нехай
в стані спокою мембрана займає деяку
область
в площині
,
з контуром
,
а після виводиться якимось чином із
стану спокою і починає коливатись так,
що всі її точки рухаються перпендикулярно
площині
(поперечні коливання мембрани).
Позначаючи
через
положення точки мембрани
в момент часу
,
через
– рівномірно розподілену зовнішню
силу, розраховану на одиницю площини,
і розглядаючи надалі тільки малі
коливання мембрани (квадратами
,
,
і їх добутками нехтуємо), можна
показати, що диференціальне рівняння
таких поперечних коливань мембрани
набуде вигляду:
(2.1)
Якщо
мембрана однорідна
то
У
випадку вільних коливань
рівняння мембрани є однорідним:
(2.2)
В
початковий момент часу необхідно
задавати початкове положення точок
мембрани та її початкові швидкості у
вигляді
(2.3).
В
точках контуру
- на границі мембрани задаються граничні
режими руху мембрани, а саме:
(2.4),
точки
контуру мембрани рухаються за заданим
законом
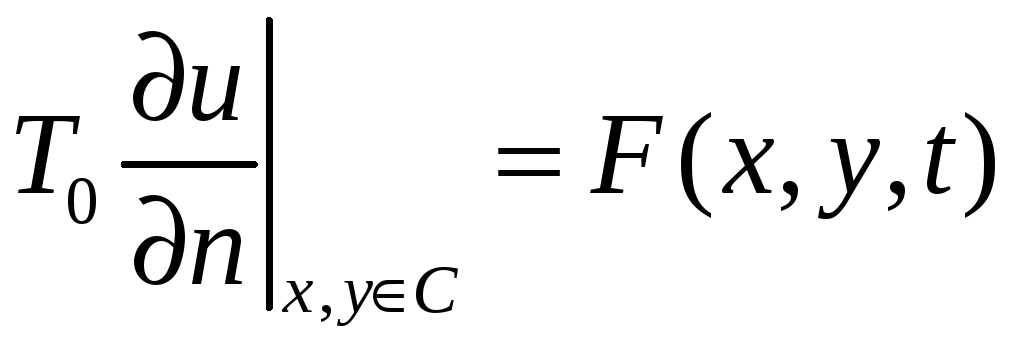(2.5),
на точки контуру діє задана сила.
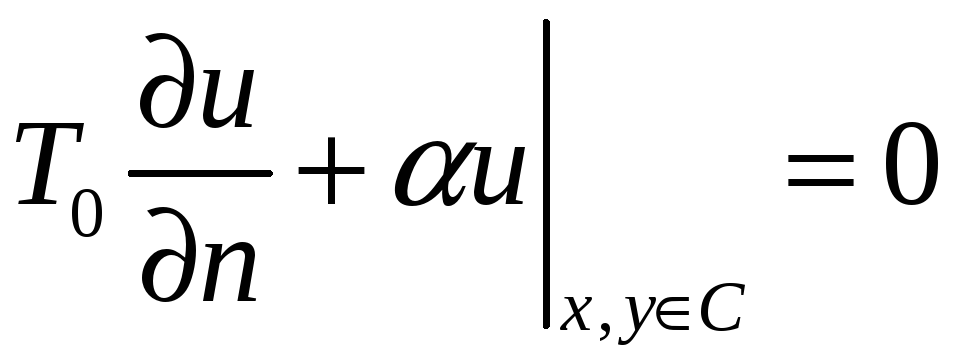(2.6),
Точки мембрани закріплені пружно.