14.Экспериментальное получение электромагнитных волн. Электромагнитные волны вдоль проводов. Стоячие электромагнитные волны в двухпроводной линии.

Источником электромагнитных волн в действительности может быть любой электрический колебательный контур ила проводник, по которому течет переменный электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором переменное электромагнитное поле создается. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры, так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное — внутри катушки индуктивности.

Электромагнитные волны, обладая широким диапазоном частот (или длин волн l=c/n, где с — скорость электромагнитных волн в вакууме), отличаются друг от друга по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны делятся на несколько видов: радиоволны, световые волны, рентгеновское и g-излучения .

Передача электромагнитной энергии вдоль проводов линии

Передача электромагнитной энергии вдоль проводов линии осуществляется электромагнитным полем, распространяющимся в окружающем провода пространстве. Провода осуществляют роль направляющих электромагнитного поля.

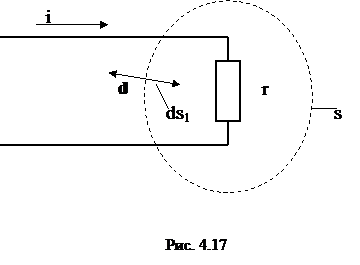
Рассмотрим произвольный приемник электромагнитной энергии, который соединен с источником посредством двухпроводной линией связи.

Окружим этот приемник вместе с частью линии замкнутой поверхностью s

Если мы рассматриваем источник, заключенный внутри поверхности s, то вектор ds имеет направление, совпадающее с внешней нормалью к этой поверхности. Если же мы хотим считать положительной энергию, передаваемую внутрь данной области сквозь поверхность s, то необходимо изменить направление положительной нормали на обратное. В данном случае в по следнем выражении следует заменить ds на ds1

15.Основные законы геометрической оптики.

Закон прямолинейного распространения света

Закон прямолинейного распространения света : в прозрачной однородной среде свет распространяется по прямым линиям. В связи с законом прямолинейного распространения света появилось понятие световой луч, которое имеет геометрический смысл как линия, вдоль которой распространяется свет. Реальный физический смысл имеют световые пучки конечной ширины. Световой луч можно рассматривать как ось светового пучка. Поскольку свет, как и всякое излучение, переносит энергию, то можно говорить, что световой луч указывает направление переноса энергии световым пучком.

Закон независимого распространения лучей

второй закон геометрической оптики, который утверждает, что световые лучи распространяются независимо друг от друга.То есть предполагается, что лучи не влияют друг на друга, и распространяются так, как будто других лучей, кроме рассматриваемого, не существует.

Отражение

Отраже́ние — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными оптическими свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн (за исключением случаев полного внутреннего отражения).

Законы отражения. Формулы Френеля

Закон отражения света — устанавливает изменение направления хода светового луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части. «угол падения равен углу отражения»

Сдвиг Фёдорова

Сдвиг Фёдорова — явление бокового смещения луча света при отражении. Отражённый луч не лежит в одной плоскости с падающим лучом.

Механизм отражения

В классической электродинамике, свет рассматривается как электромагнитная волна, которая описывается уравнениями Максвелла. Световые волны, падающие на диэлектрик вызывают малые колебания диэлектрической поляризации в отдельных атомах, в результате чего каждая частица излучает вторичные волны во всех направлениях.

16. Условия необходимые для получения интерференционной картины. Когерентность и монохроматичность световых волн. Время и длина когерентности. Радиус когерентности.

Интерференцию света можно объяснить, рассматривая интерференцию волн Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.

монохроматические волны - не ограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны.

Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга tког называется временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т. е. tког < t. Прибор обнаружит четкую интерференционную картину лишь тогда, когда время разрешения прибора значительно меньше времени когерентности накладываемых световых волн.

Если волна распространяется в однородной среде, то фаза колебаний в определен ной точке пространства сохраняется только в течение времени когерентности tког. За это время волна распространяется в вакууме на расстояние lког = ctког, называемое длиной когерентности (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.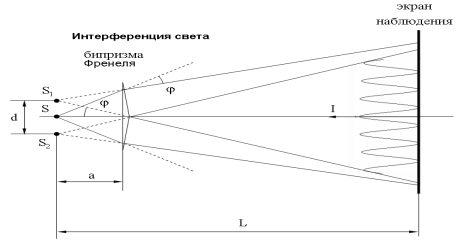

Чем ближе волна к монохроматической, тем меньше ширина Dw спектра ее частот и, как можно показать, больше ее время когерентности tког, следовательно, и длина когерентности lког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временной когерентностью.

Наряду с временной когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры и взаимное расположение которых позволяют (при необходимой степени монохроматичности света) наблюдать интерференцию, называются пространственно-когерентными. Радиусом когерентности (или длиной пространственной когерентности) называется максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. Таким образом, пространственная когерентность определяется ради усом когерентности.

Радиус когерентности

Условия интерференции

Таким образом, необходимое условие наличия четкой интерференционной картины (в случае квазимонохроматических волн с постоянными амплитудами) – разность фаз двух складываемых колебаний сохраняет свое значение за время усреднения, хотя сама фаза может меняться (хотя бы и хаотически и в больших пределах).