
- •1.Гармонические колебания. Дифференциальное уравнение гармонических колебаний, его решения. Превращение энергии при колебаниях. Векторная диаграмма.
- •2. Гармонический осциллятор. Пружинный и математический маятники. Физический маятник. Приведенная длина физического маятника. Центр качания.
- •3.Электрический колебательный контур. Уравнение собственных колебаний ,формула Томсона. Взаимопревращения энергии в контуре.
- •4.Сложение колебаний одного направления. Понятие когерентности.
- •5. Сложение взаимно перпендикулярных колебаний. Типы поляризованных колебаний. Фигуры Лиссажу.
- •6.Свободные затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решения. Времярелаксации. Логарифмический декремент затухания. Добротность.
- •Время установления колебаний в контуре
- •8. Вынужденные колебания в электрических цепях. Дифференциальное уравнение колебаний. Векторная диаграмма. Полное сопротивление цепи переменного тока. Резонанс напряжений.
- •9. Волновое движение. Виды волн. Уравнение бегущей волны. Характеристика волн. Длина волны. Волновое число. Одномерное волновое уравнение. Скорость упругих волн.
- •Скорость волны.
- •10. Принцип суперпозиции волн. Волновой пакет. Фазовая и групповая скорости. Понятие о дисперсии.
- •11. Стоячие волны, их особенности. Уравнение стоячей волны. Пучности и узлы стоячей волны. Спектр частот стоячих волн в простых системах.
- •12. Основы теории Максвелла. Вихревое электрическое поле. Полная система уравнений Максвелла. Существование электромагнитных волн. Свойства электромагнитных волн.
- •13 Энергия электромагнитных волн. Вектор Умова-Пойтинга. Давление и импульс электромагнитного поля. Шкала электромагнитных волн.
- •14.Экспериментальное получение электромагнитных волн. Электромагнитные волны вдоль проводов. Стоячие электромагнитные волны в двухпроводной линии.
- •15.Основные законы геометрической оптики.
- •17. Способы получения интерференционной картины света. Условия максимума и минимума при интерференции. Ширина интерференционной полосы. Опыт Юнга.
- •18. Интерференция света в тонких пленках. Полосы равной толщины. Полосы равного наклона. Кольца Ньютона. Применение интерференции света. Интерферометры.
- •19. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Прямолинейное распространение света. Зонная пластинка.
- •20.Дифракция света на щели. Дифракция Фраунгофера. Влияние ширины цели на картинку дифракции. Дифракционная решетка.
- •22.Дисперсия света. Нормальная и аномальная дисперсия. Групповая скорость. Классическая электронная теория дисперсии света. Показатель преломления вещества.
- •23.Двойное лучепреломление. Обыкновенный и необыкновенные лучи. Одноосные кристаллы. Анизотропия кристаллов. Явление дихроизма. Поляроиды и поляризационные призмы. Призма Николя.
- •24.Искусственная оптическая анизотропия. Одностороннее сжатие.
3.Электрический колебательный контур. Уравнение собственных колебаний ,формула Томсона. Взаимопревращения энергии в контуре.
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания
Резонансная частота контура определяется так называемой формулой Томсона:
![]()
![]()
Колебательный RLC-контур.
Уравнение свободных затухающих колебаний можно получить, исходя из того, что в отсутствии внешнего источника напряжения, сумма падений напряжений на индуктивности, емкости и сопротивлении равна нулю для любого момента времени:
![]()
Полная энергия колебательного контура
 ;
;
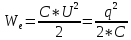 ;
;

где We — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, Wm — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.
4.Сложение колебаний одного направления. Понятие когерентности.
Когерентность (от латинского cohaerens — находящийся в связи), согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называются когерентными, если разность их фаз остаётся постоянной во времени и при сложении колебаний определяет амплитуду суммарного колебания. Два гармонических (синусоидальных) колебания одной частоты всегда когерентны. Гармоническое колебание описывается выражением:
х = A cos (2pvt + j), (1)
где х — колеблющаяся величина (например, смещение маятника от положения равновесия, напряжённость электрического и магнитного полей и т.д.). Частота гармонического колебания, его амплитуда А и фаза j постоянны во времени. При сложении двух гармонических колебаний с одинаковой частотой v, но разными амплитудами A1 и А2 и фазами j1 и j2, образуется гармоническое колебание той же частоты. Амплитуда результирующего колебания:
![]() (2)
(2)
может изменяться в пределах от A1 + А2 до А1 — А2 в зависимости от разности фаз j1 — j2 (). Интенсивность результирующего колебания, пропорциональная Ар2 также зависит от разности фаз.
Сложение колебаниё одного направления и одинаковой частоты.
Рассмотрим сложение двух гармонических колебаний х 1 и x 2 одного направления и одинаковой частоты:
![]() ,
,
![]() (1)
(1)
Оба колебания представим с помощью векторов A 1 и А 2 . Используя правила сложения векторов можно найти результирующий вектор А, представляющий собой сумму двух векторов A 1 и А 2 .
 Вектор
A
представляет
собой результирующее колебание, потому
что из рисунка видно, что проекция этого
вектора на ось x равна сумме проекций
складываемых векторов:
Вектор
A
представляет
собой результирующее колебание, потому
что из рисунка видно, что проекция этого
вектора на ось x равна сумме проекций
складываемых векторов:
![]()
Вектор A вращается с той же угловой скоростью ω 0 , как и векторы А 1 и А 2 , так что сумма x 1 и х 2 является гармоническим колебанием с частотой (ω 0 , амплитудой A и начальной фазой α . Используя теорему косинусов получаем, что
 (2)
(2)
![]()
