38. Статистична перевірка гіпотез

Нехай у (статистичному) експерименті спостерігається реалізація  деякої випадкової величини X, розподіл якої  невідомий повністю чи частково. Тоді будь-яке твердження, що стосується , називається статистичною гіпотезою. Гіпотези розрізняються за видом припущень, що містяться в них:Статистична гіпотеза, що однозначно визначає розподіл , тобто , де  якийсь конкретний закон, що має назву простий.Статистична гіпотеза, що стверджує, що розподіл  належить до деякої сім'ї розподілів, тобто виду , де  - сім'ю розподілів, що має назву складна.На практиці зазвичай потрібно перевірити якусь конкретну і, як правило, просту гіпотезу H₀. Таку гіпотезу прийнято називати нульовою. При цьому паралельно розглядається гіпотеза, що протирічить їй H₁, що називається конкуруючою або альтернативною.Висунута гіпотеза потребує перевірки, яка здійснюється статистичними методами, тому гіпотезу називають статистичною. Для перевірки гіпотези використовують критерії, що дозволяють прийняти або спростувати гіпотезу.В більшості випадків статистичні критерії засновані на випадковій вибірці  фіксованого об'єму  з розподілу . У послідовному аналізі вибірка формується в ході самого експерименту і тому її об'єм є випадковим величиною..Етапи перевірки статистичних гіпотез:Формулювання основної гіпотези H₀ і конкуруючої гіпотези H₁. Гіпотези повинні бути чітко формалізовані в математичних термінах.Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези.Розрахунок статистики ϕ критерію такий, що:її величина залежить від початкової вибірки ;по її значенню можна зробити висновки про істинність гіпотези H₀;сама статистика ϕ повинна підкорятися якомусь невідомому закону розподілу, так як сама ϕ є випадковою в силу випадковості .Побудова критичної області. З області значень ϕ виділяємо підмножину  таких значень, по яким можна судити про суттєвість розбіжностей з припущенням. Її розмір вибирається таким чином, щоб виконувалась рівність . Ця множина  і називається критичною областю.Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику ϕ і по попаданню (або непопаданню) в критичну область  виноситься ухвала про відкидання (або ухвалення) висунутої гіпотези H₀.

39. Дії над множинами

За допомогою декількох називаються її k-елементні впорядковані підмножини, що відрізняються тільки порядком елементів (якщо всі елементи заданої множини різні – маємо перестановки без повторень, а якщо в заданій множині елементи можуть повторюватися, серед яких повторюється раз, разів, …, – разів, то маємо перестановки з повтореннями).де -без повторень, -з повтореннями.

Комбінаціями (сполученнями) без повторень з n елементів по називаються будь-які k-елементні підмножини n-елементної множини, що різняться між собою принаймні одним елементом. Порядок елементів у сполученні не є істотним.Комбінаціями (сполученнями) з повтореннями з n елементів (необов’язково різних) по називаються набори цих елементів, до кожного з множин можна будувати нові множини або, як кажуть, робити операції над множинами. Ми розглянемо такі операції над множинами: об'єднання, перетин, різниця множин, доповнення множини. Всі розглянуті операції над множинами ми будемо ілюструвати на діаграмах Ейлера-Венна.  Об'єднання множин -Об'єднанням А  У множин А і В називається множина, яка складається з усіх елементів, що належать хоча б одній з множин А чи В.  Символічна запис цього визначення: А  В = {х | х  А чи х  У}.  Тут союз «або» розуміється в сенсі «неразделітельного або», тобто не виключається, що х може належати і А і В. Відзначимо, що в такому випадку елемент х, що входить в обидва множини А і В, входить до їх об'єднання тільки один раз (оскільки для множини не має сенсу говорити про те, що елемент входить в нього кілька разів).  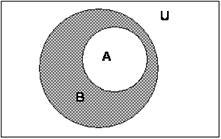Пояснимо визначення об'єднання множин за допомогою діаграми Ейлера-Венна:  На діаграмі об'єднання множин А і В виділено штрихуванням. Якщо безліч А визначається характеристичним властивістю Р (х), а безліч В - характеристичним властивістю Q (х), то А  В складається з усіх елементів, які мають, принаймні, одним з цих властивостей. Перетин множин  Перетином А ∩ В множин А і В називається множина, яка складається з усіх елементів, що належать одночасно кожному з множин А і В.  Символічна запис цього визначення: А ∩ В = {х | х  А і х  У}.  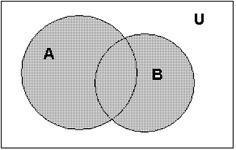Пояснимо визначення перетину множин за допомогою діаграми Ейлера-Венна:  А ∩ В  На діаграмі перетин множин А і В виділено штрихуванням.  Якщо безліч А задається характеристичним властивістю Р (х), a безліч По-властивістю Q (х), то в А ∩ В входять елементи, одночасно володіють і властивістю Р (х), і властивістю Q (х).  Приклади перетинань двох множин:  1) Нехай А = {2; 5; 7; 8}, В = {3, 5, 6, 7}. Тоді А ∩ В = {5; 7}. 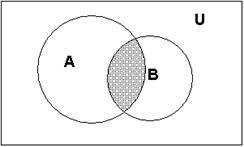Різниця множин  Різницею А \ У множин А і В називається множина, яка складається з усіх елементів множини А, які не належать безлічі В, тобто  А \ В = {х | х  А і х  У},  що можна пояснити на діаграмі Ейлера-Венна наступним чином:  На діаграмі різниця А \ В виділена штрихуванням.  Приклади різниць множин:  1. Нехай А = {1, 2, 5, 7}, В = {1, 3, 5, 6}. Тоді А \ В = {2; 7}, а В \ А = {3, 6}. 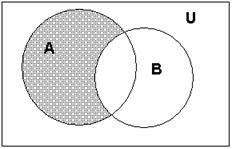Доповнення множини  Нехай безліч А і В такі, що А  В. Тоді доповненням множини А до множини В називається різниця В \ А. У цьому випадку застосовується позначення С _B А = В \ А. Якщо в якості безлічі У береться універсальне безліч U, то застосовується позначення СА = С _U А = U \ А і таке безліч просто називають доповненням множини А. Таким чином, символічна запис визначення доповнення безлічі буде наступною:  СА = {x | x  A}.  На діаграмах Ейлера-Венна можна так пояснити визначення С _В А і СА: