41. Метод максимальної правдоподібності побудови точкових оцінок.

Даний метод був запропонований Фішером. Нехай випадкові величини є дискретними. Припустимо,що вид закону розподілу у нас заданий, але невідомий параметр , потрібно знайти . Позначимо, що в результаті випробувань величина прийме значення: , - реалізація вибірки. В якості точкової оцінки приймають таке його значення при якому функція правдоподібності досягає максимуму, тоді оцінку називають оцінкою максимальної правдоподібності. - логарифмічна функція правдоподібності. Шукаємо точку мах функції наступним чином: 1)знаходимо похідну: ; 2) прирівняємо її до нуля і знаходимо корінь даного рівняння, це рівняння правдоподібності; 3) знаходимо другу похідну , якщо друга похідна від’ємна, то - точка мах. Знайдену точку мах приймають в якості оцінки мах правдоподібності параметра .

42. Оцінки максимальної правдоподібності.

В якості точкової оцінки приймають таке його значення при якому ф-ція правдоподібності досягає максимуму. Тоді оцінку наз. оцінкою макс. правдоподібності.

43. Функція правдоподібності для неперервної випадкової величини, для дискретної в. в., р-ня правдоподібності.

Ф-цією правдоподібності дискрет. в. в. наз. ф-цію , де .

Ф-цією правдопод. Неперервної в. в. наз ф-цію , де .

44. Логарифмічна ф-ція правдоподібності.

Наз ф-цію .

45. Гамма-розподіл

В.в. має гамма розподіл з параметрами якщо її щільність має вигляд:

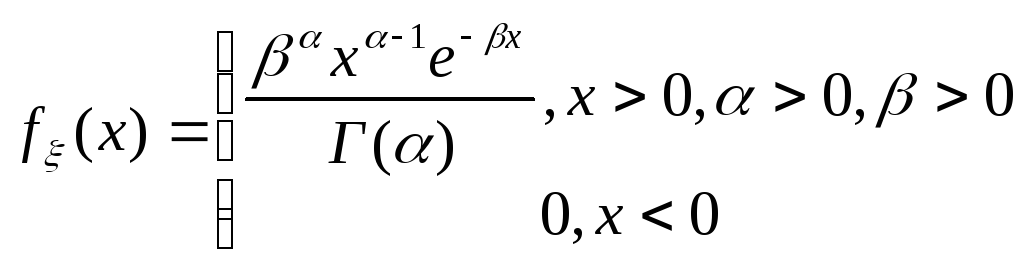
Де Г-ф-ція визначається як

46. розподіл

Задається щільністю:

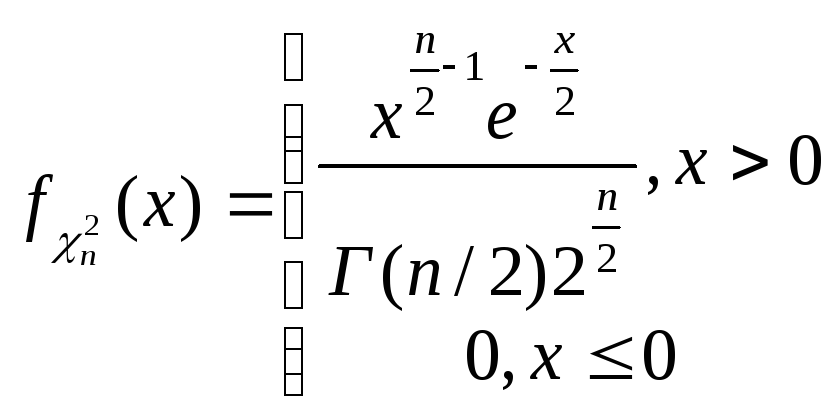
n-кількість ступенів свободи n=1,2… .

- квантіль.

47. Розподіл Стьюдента

В.в. має -розподіл Стьюдента, якщо її щільність задається формулами:

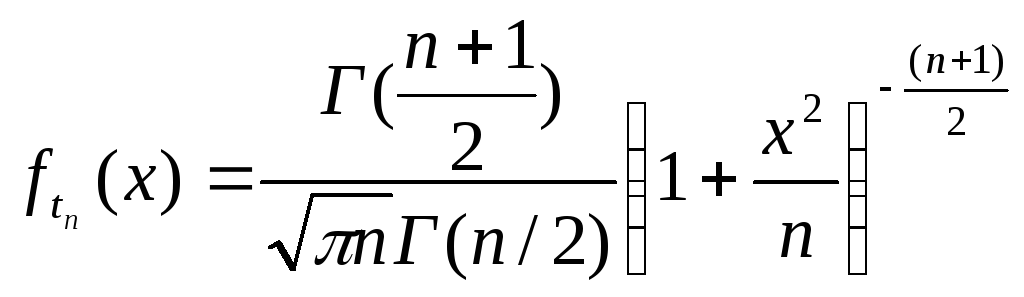при .

n-кількість ступені свободи

48.Розподіл Фішера-Снедекора

Нехай є дві незалежні в.в , що мають розподіл з n ступенями свободи.

має розподіл Фішера-Снедекора з степенями свободи.

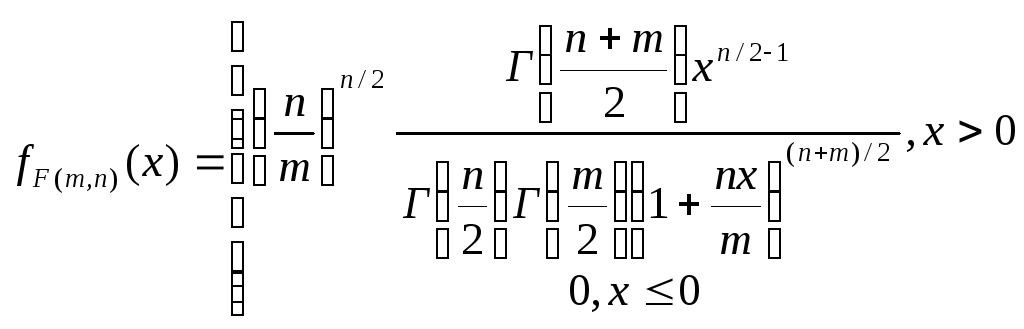
49. Теорема про розподіл , де з ступенями свободи i=

Нехай у нас є вип. Величин, які є взаємонезалежними та мають розподіл

Відповідно з ступенями свободи, тоді мають розподіл з ступенями свободи.

50. Теорема про розподіл , де (0,1)

Нехай у нас є взаємонезалежні вип.. величини, що мають один і той самий стандартний нормальний розподіл N(0,1),, то сума квадратів має розподіл з n ступенями свободи.

51 Квантіль розподілу випадкової величини, що відповідає ймовірності називається таке значення , яке випадкова величина не переважає з ймовірності : .

52. Теорема про розподіл величини де(0,1) η розподіл з n ступенем свободи.

Нехай є дві незалежні вип. величини при чому має нормальний стандартний розподіл (0,1) η, тоді велечина

53. Задача точності точкової оцінки

Оцінка невідомого параметра одним числом називається точковою, але існує ряд задач, де потрібно знайти не тільки значення, яке б підходило нам, але й оцінити його точність та надійність. Така задача особливо актуальна, коли в нас мала кількість спостережень і коли точкова оцінка в значній мірі випадкова і наближення параметра даною оцінкою може призвести до помилок. Для визначення точності в математичній статистиці користуються так званим довірчим інтервалом, тобто виникає задача точності визначення ступеня близькості між істинним значенням параметра та його точковою оцінкою.

54. Довірча ймовірність

. Величина це як ймовірність того, що випадковий інтервал накриває точку .Ймовірність будемо називати довірчою ймовірністю,

55. Довірчий інтервал

Інтервал - називаємо довірчим інтервалом.

56. Довірчі границі

Інтервал , який визначається, як має випадкові кінці, їх називають довірчими границями.

57. Точність точкового оцінювання параметру.

Точність точкового оцінювання параметра за допомогою , що гарантується з довірчою ймовірністю позначаються як та називають гранично допустимим відхиленням від , яке не перевищує в наступних випадках із 100.

58. Побудова асимптотичної найкоротших довірчих інтервалів.

Ефективні та асимтотично ефективні оцінки призводять до найкоротших інтервалів. ; ; . Якщо у нас ця функція є неперервною, то є збіжність, яка визначається: ; 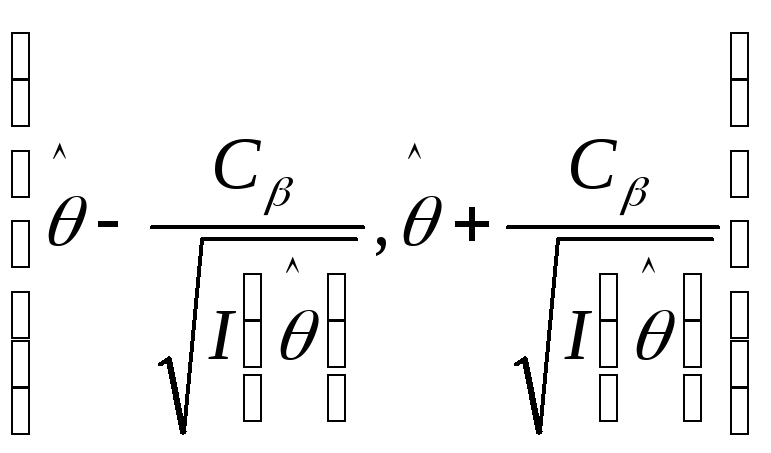- асимтотично найкоротший інтервал.

59. Побудова довірчих інтервалів для математичного сподівання нормального розподілу при відомій дисперсій.

, де .

60. Побудова довірчих інтервалів для дисперсії нормального розподілу, що коли математичне сподівання а невідоме.

.

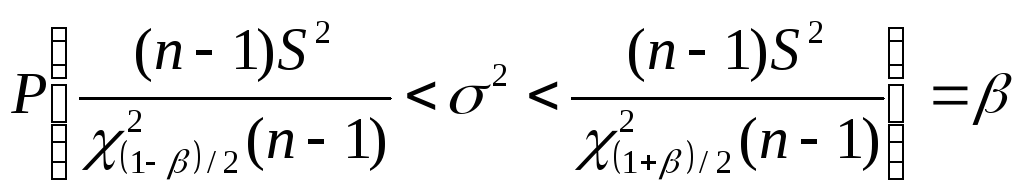61. Довірчий інтервал для дисперсії коли математичне сподівання відоме.

Оцінкою максимальної правдоподібності для дисперсії буде

Розглянемо випадкову величину дана величина має розподіл із n ступенями свободи. Цю випадкову вел можна представити як :

Довірчий інтервал матиме вигляд:

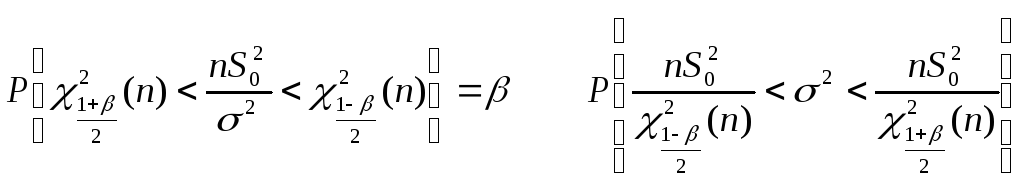
62. Побудова довірчих інтервалів для математичного сподівання нормального розподілу при невідомої дисперсії.

Розглянемо випадкову величину , що має розподіл Студента із (n-1) степенями свободи.

Знайдемо число , яке б задовольняло рівність

Перепишемо вище наведену рівність і отримаємо довірчий інтервал

Зауважимо, якщо n>30 то розподіл Студента прямує до нормального розподілу.

63. Статистична гіпотеза – це деяке твердження(припущення) про вид розподілу випадкової величина, яке потрібно перевірити за даними вибіркової сукупності.

64. Гіпотеза або альтернатива називається простою, якщо їй відповідає лише одне значення параметра .

Приклад: .

65. Гіпотеза або альтернатива називається складною, якщо їй відповідає не одне значення параметра .

Приклад : .

66.Критерій перевірки гіпотези – називають деяку функцію , яка характеризує степінь відповідності вибіркових даних статистичній гіпотезі.

67. Область прийняття гіпотези – це замкнутий інтервал дійсної осі такий, що при попаданні критерію, що підраховується за даними вибірки, в дану область гіпотеза приймається. Має вигляд .

68. Критична область – це інтервал або інтервали дійсної осі такі, що при попаданні критерію, що підраховується за даними вибірки, в дану область гіпотеза не приймається. Складається із тих точок, що не увійшли в область прийняття рішення.

69. Помилкою першого роду називають відхилення справедливої гіпотези, тобто ми не приймаємо гіпотезу коли вона є справедливою.

70.Помолкою другого роду називають прийняття гіпотези, коли вона не справджується.

71.Рівнень значущості – це максимально допустима ймовірність помилок першого роду, позначається . Заданий рівень значущості забезпечується за рахунок вибору критичної області і області прийняття рішень, вибирається таким чином .

72.Функція потужності критерію називають ймовірність відхилення основної гіпотези, яка обрахована, що істинне значення параметра .

- ймовірність підрахування даного параметра .

73. За нульову гіпотезу слід приймати те припущення неправильне відхилення якого приводить до менш незначних наслідків.

74. Критичним рівнем значущості називається максимальний рівень значущості при якому гіпотеза приймається.