- •Поняття математичної статистики
- •Основні задачі мат. Статистики
- •Статистичний розподіл вибірки
- •23. Як визначаються мода та медіана у випадку, коли дані вибірки згруповані по інтервалах?
- •25. Точкова оцінка.
- •26. Основні властивості оцінок.
- •28. Конзистентність (слушність) оцінки.
- •29. Ефективність оцінки.
- •31.Чи є оцінка для дисперсії незміщеною, консистентною та ефективною?
- •32.Теорема про незміщеність емпіричних початкових моментів.(Доведення)
- •41. Метод максимальної правдоподібності побудови точкових оцінок.
- •75. Етапи перевірки статистичних гіпотез:
- •76. Визначення області прийняття гіпотези та критичну область для гіпотези при альтернативі
- •77. Визначення області прийняття гіпотези та критичну область для гіпотези при альтернативі .
- •78. Визначення області прийняття гіпотези та критичну область для гіпотези (при альтернативі
- •103. Побудова довірчого інтервалу для
- •104. Вибіркова коваріація
- •105. Вибірковий коефіцієнт кореляції, властивості
-
Поняття математичної статистики
Мат. Статистика – це наука, яка вивчає методи збору, класифікації та обробки даних спостереження (статистичних даних) з метою отримання на їх основі обгрунтованих висновків.
Мат. Статистика базується на поняттях та методах теорії ймовірностей, причому в деякому розумінні мат. Статистика розв’язує задачі обернені задачам теорії ймовірностей, тобто мат. Статистика виявляє структуру статистичних моделей за результатами проведених спостережень.
-
Основні задачі мат. Статистики
А) Розробка методів збору і групування статистичних даних, отриманих в результаті спостережень або ж опрацювання статистичних звітів чи даних у результаті спеціально поставлених експериментів.
Б) Розробка методів аналізу статистичних даних залежно від мети досліджень:
— оцінка невідомої ймовірності випадкової події на основі спостережень; оцінка невідомої функції розподілу випадкової величини за даними, які отримані в результаті спостережень; оцінка параметрів розподілу, вид якого відомий; оцінка залежності в.в. від однієї або декількох вип. величин.
-
точність точкового оцінювання, тобто це задача оцінювання близькості між точковою оцінкою параметра та істинним значенням параметра.
-
перевірка статистичних гіпотез про вид невідомого розподілу або величину параметрів розподілу вид якого невідомий.
-
Поняття генеральної сукупності
Генеральна сукупність – це сукупність всіх значень деякої ознаки досліджуваних об’єктів.
-
Що таке вибірка?
Вибірковою сукупністю або вибіркою називається сукупність випадково відібраних об’єктів з генеральної сукупності.
-
Об’єм сукупності
Об’єм сукупності – це число об’єктів цієї сукупності
-
Основні способи відбору
-
Відбір, що не потребує розподілу генеральної сукупності на частини
-
Простий випадковий відбір без повернення
-
Простий випадковий повторний відбір
-
-
Відбір, в якому генеральна сукупність розбивається на частини
-
Типовий відбір
-
Механічний відбір
-
Серійний відбір
-
Простий відбір – це при якому об’єкти вибираються по одному із всієї генеральної сукупності.
Типовий відбір – відбір, при якому об’єкти вибираються з кожної типової частини.
Механічний відбір – це при якому всю генеральну сукупність ділять на декілька груп і з кожної групи вибирають по одному об’єкту.
Серійний відбір – це при якому об’єкти вибираються не по одному, а серіями.
-
Статистичний розподіл вибірки
Статистичний розподіл вибірки – це перелік варіант та відповідних їм частот або відносних частот. У випадку, коли обсяг дискретного рядку достатньо великий, то його можна перетворити на інтервальний, тобто статистичний розподіл можна задавати у вигляді послідовності інтервалів та відповідних їм частот (за частоту приймають в даному випадку суму частот елементів вибірки, які попали в даний інтервал).
-
Визначення частоти
Число, яке показує скільки разів зустрічалась варіанта хі називається частотою і позначається ni.
-
Визначення відносної частоти
Відносна
частота показує долю конкретної варіанти
у вибірці.
![]()
-
Визначення накопичувальної частоти
Накопичувальна частота – це сумарна частота варіант, які розміщені у варіаційному ряді нижче відповідної варіанти (якщо ряд дискретний) або верхнього кінця проміжку (якщо ряд інтервальний).
-
Варіаційний ряд, елемент вибірки
Впорядкована
за зростанням послідовність
![]() називається варіаційним рядом. Елемент
називається варіаційним рядом. Елемент
![]() називається і-м
членом варіаційного ряду або і-ю
варіантою або і-ю
впорядкованою статистикою.
називається і-м
членом варіаційного ряду або і-ю
варіантою або і-ю
впорядкованою статистикою.
-
Полігони частот та відносних частот
Полігон
частот – ламана лінія, яка відображає
залежність між варіантою та частотою
і утворюється шляхом з’єднання прямим
лініями точок (![]() ),
де
),
де
![]() - відповідно варіанта і її частота.
- відповідно варіанта і її частота.
Полігон
відносних частот – ламана лінія, яка
відображає залежність між варіантою і
відносною частотою і утворюється шляхом
з’єднання прямими лініями точок
![]() ,
де
,
де
![]() -
відповідно варіанта і її відносна
частота.
-
відповідно варіанта і її відносна
частота.
-
Гістограми частот і відносних частот
Гістограма
частот – це функція, яка має сходинковий
характер та складається з прямокутників
основами яких є інтервали довжиною h,
а висоти дорівнюють відношенню
![]() .
.
Гістограма
відносних частот – це функція, яка має
сходинковий характер і складається з
прямокутників, основами яких є інтервали
довжиною h,
а висоти дорівнюють відношенню
![]() .
.
-
Основні типи параметрів, що піддаються оцінці
Математичне сподівання, дисперсія, функція розподілу, функція щільності
-
Вибіркові характеристики вибірки, коли дані не повторюються
Вибірковий
момент r-го
порядку

Вибіркове
середнє
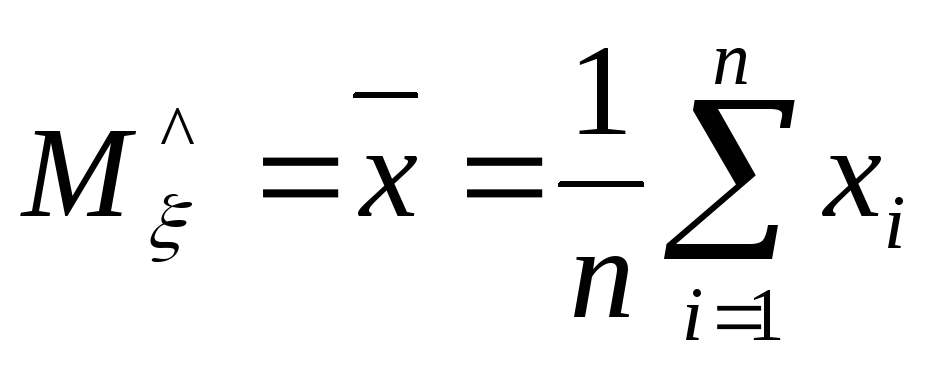
Вибіркова
дисперсія
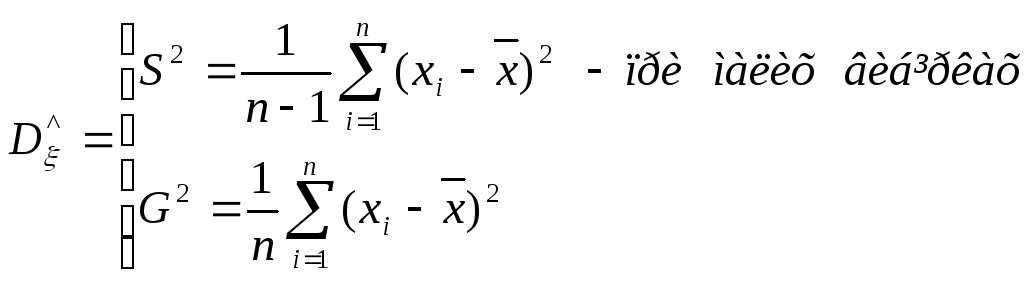
-
Вибіркові характеристики вибірки, коли дані повторюються
Вибірковий
момент r-го
порядку

Вибіркове
середнє
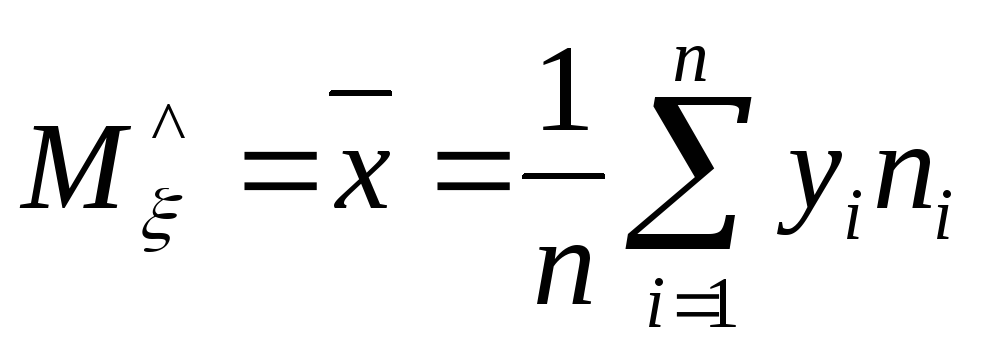
Вибіркова
дисперсія

-
Означення емпіричної функції розподілу
Нехай
нам відомо статистичний розподіл в.в.
![]() .
Позначимо
.
Позначимо
![]() випадкову величину, яка дорівнює
кількості елементів вибірки, які менші
за х
і покладемо
випадкову величину, яка дорівнює
кількості елементів вибірки, які менші
за х
і покладемо
![]() ,
де дане відношення визначає відносну
частоту події, де
,
де дане відношення визначає відносну
частоту події, де
![]()
Отже,
емпіричною функцією розподілу (функцією
розподілу вибірки) в.в.
![]() називається функція
називається функція
![]() ,
що визначає відносну частоту події, де
,
що визначає відносну частоту події, де
![]() .
.
-
Основні властивості емпіричної функції розподілу
-
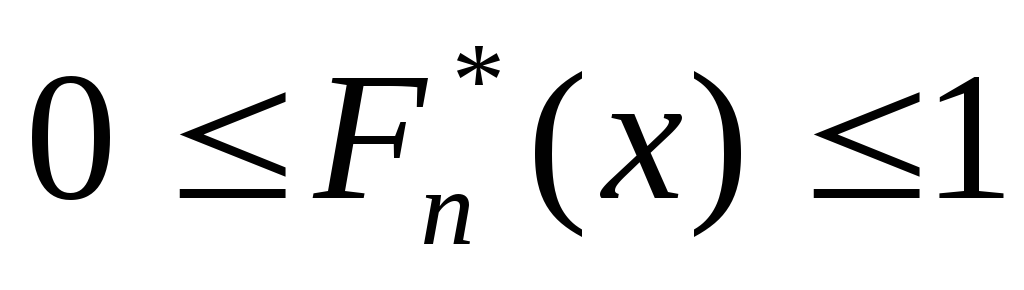
-
 -
неспадна сходинкова функція
-
неспадна сходинкова функція -
 ,
де
,
де
 -
найменша варіанта
-
найменша варіанта -
 ,
де
,
де
 -
найбільша варіанта
-
найбільша варіанта
-
-
Як визначається функція розподілу, якщо всі компоненти вибірки різні?

-
Як визначається емпірична функція розподілу, якщо всі компоненти вибірки повторюються?

21.Як визначається мода у випадку, коли дані вибірки повторюються?
У випадку коли дані вибірки повторюються мода визначається наступним чином:
Складаємо варіаційний ряд і визначаємо варіанту яка найчастіше повторюється.
22. Як визначається медіана у випадку, коли дані вибірки повторюються?
Складаємо
варіаційний ряд і шукаємо варіанту яка
ділить цей ряд пополам. Якщо кількість
варіант не парна, то медіаною є елемент
![]() (n=2k)
(n=2k)
Якщо
кількість варіант є парною,то медіаною
є