Локальная теорема Муавра-Лапласа.

В условиях схемы Бернулли т.е. при проведении n независимых испытаний с двумя исходами, в каждом из которых вероятность появления события А постоянна и равна p (0< p<1), а вероятность появления противоположного события равна q=1–p, для (вероятности того, что в этих испытаниях событие А наступит ровно m раз) имеет место приближенное равенство

, (6.3)

где , .

Для функции составлены таблицы, которые присутствуют во всех справочниках и пособиях по теории вероятностей. Они позволяют не вычислять значение в каждой конкретной задаче. При пользовании таблицами нужно учитывать, что функция четная, т.е. =. Поэтому значения этой функции при отрицательных x в таблице не приводятся.

Вы найдете таблицу значений в приложении, расположенном в конце данного пособия.

Формула (6.3) позволяет достаточно точно вычислить , когда n велико, а p не очень близко к 0 или к 1. Этой формулой обычно пользуются, если .

Пример 6.5. 95% всей продукции некоторой фабрики составляет продукция высшего сорта. Определим вероятность того, что из взятых на проверку 500 изделий 480 окажутся высшего сорта.

По условию задачи мы находимся в рамках схемы Бернулли, где , , , . Поскольку n достаточно велико, и , мы можем использовать формулу (6.3) для вычисления искомой вероятности. Тогда , . По таблице значений находим . Следовательно, . Как мы видим, полученная вероятность достаточно мала.

На практике часто в условиях схемы Бернулли требуется вычислить вероятность того, что событие А наступит не менее k₁ и не более k₂ раз, т.е. вероятность . В этом случае приближенную формулу дает интегральная теорема Муавра - Лапласа.

Интегральная теорема Муавра-Лапласа.

В условиях схемы Бернулли т.е. при проведении n независимых испытаний с двумя исходами, в каждом из которых вероятность появления события А постоянна и равна p (0< p<1), а вероятность появления противоположного события равна q=1–p, для (вероятности того, что в этих испытаниях событие А наступит не менее k₁ и не более k₂ раз) имеет место приближенное равенство

, (6.4)

где , , .

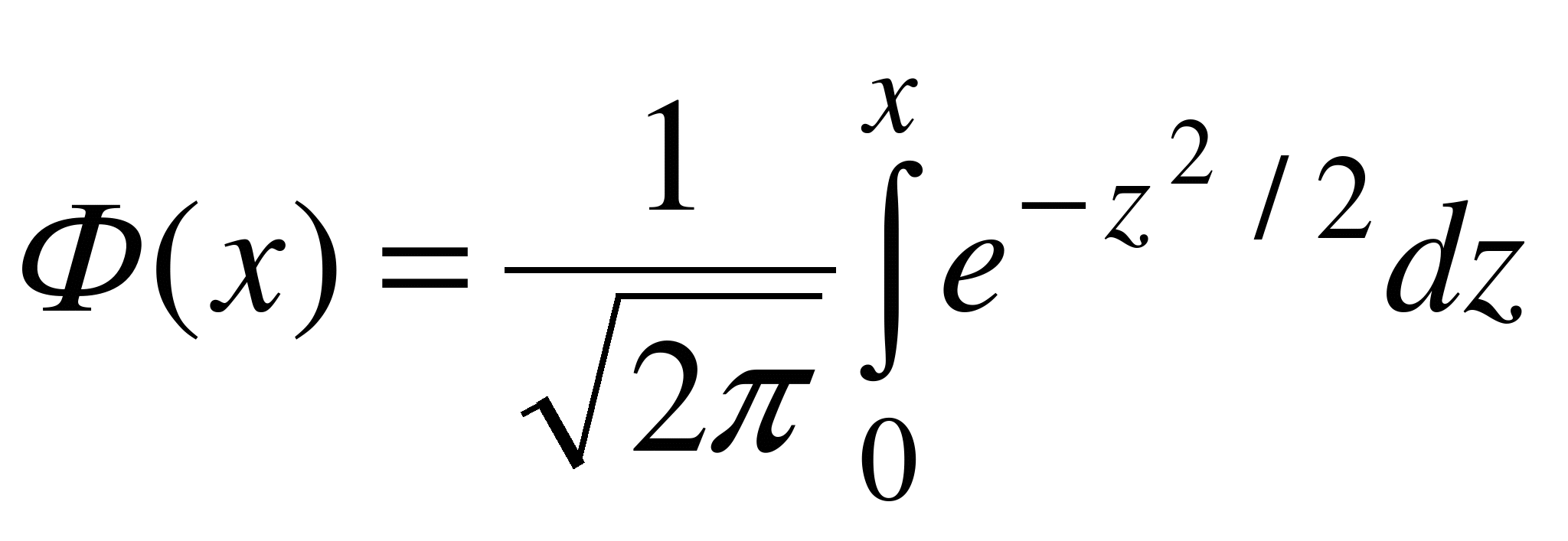Функция называется функцией Лапласа. Для нее также составлены таблицы, которые можно найти во всех справочниках и пособиях по теории вероятностей. При пользовании таблицами нужно учитывать, что функция нечетная, т.е. =. Кроме того, обычно в таблицах указаны значения функции Лапласа для значений x от 0 до 5; при x > 5 полагают =0,5.

Таблицу значений Вы также найдете в приложении.

Замечание. В некоторых учебниках функцией Лапласа называют функцию 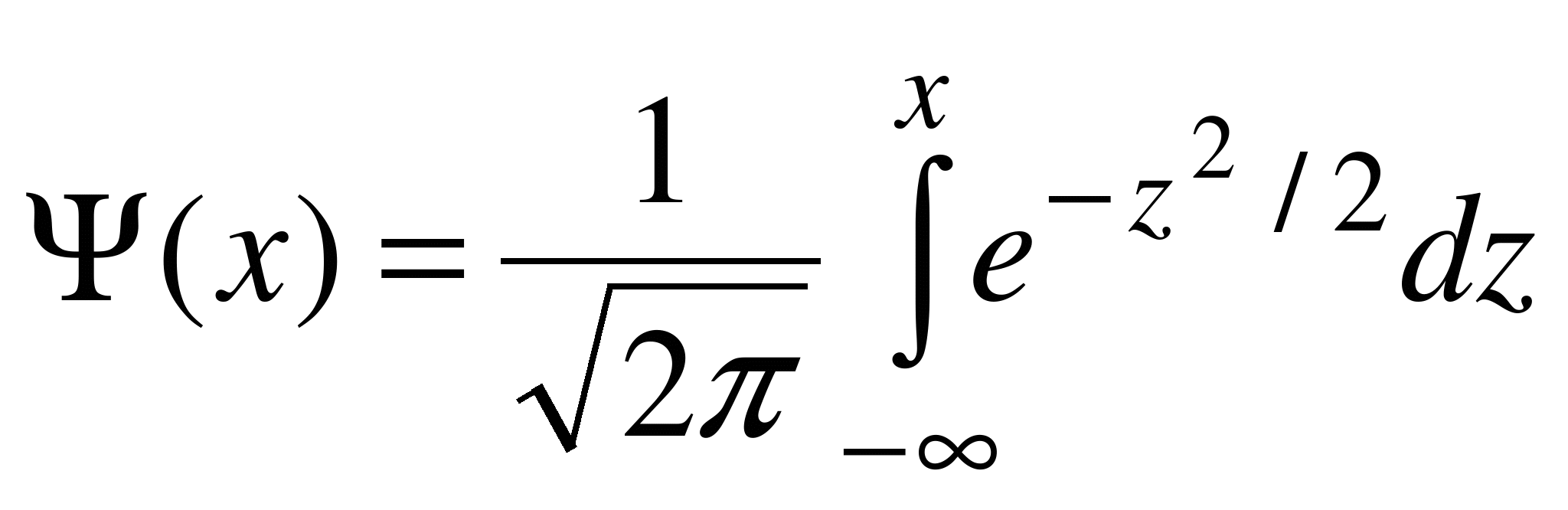(от функции она отличается нижним пределом интегрирования). При этом все формулы интегральной теоремы сохраняются, таблицы для вычисления приводятся в этих учебниках, но функция не обладает свойством нечетности. Для вычисления значений при отрицательных x нужно использовать соотношение .

Пример 6.6. В условиях примера 5.5 найдем вероятность того, что от 470 до 490 изделий окажутся высшего сорта.

По условию задачи , k₁=470, k₂=490, , . Поскольку n достаточно велико, и , мы для вычисления искомой вероятности используем формулу (6.4). Проводя вычисления, получаем: , . По таблице значений функции Лапласа находим , .

Следовательно, 0,8465.

Доказательства локальной и интегральной теорем Лапласа достаточно сложны и объемны, поэтому мы привели здесь лишь формулировки теорем и примеры, иллюстрирующие их использование.

Приведем также одно важное следствие из интегральной теоремы Муавра-Лапласа, а именно формулу для вычисления вероятности осуществления неравенства , то есть вероятности того, что отклонение относительной частоты m/n наступления события А от его вероятности p не превышает по абсолютной величине некоторого заданного числа :

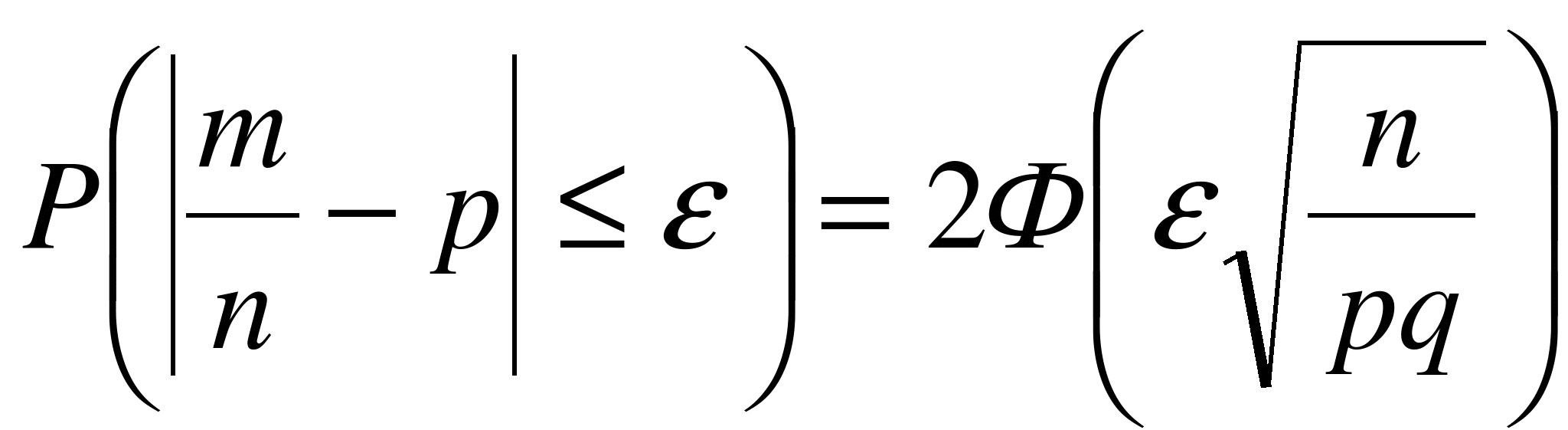. (6.5)

Равенство (6.5) легко выводится из (6.4) и носит название формулы вероятности отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Пример 6.7. Вероятность появления события А в каждом из независимых испытаний равна 0,6. Найдем вероятность того, что относительная частота появления события А в 1000 испытаниях отклонится от его вероятности по абсолютной величине не более, чем на 0,02.

Согласно условию задачи n=1000, p=0,6, q=1-p=0,4, =0,02. Значит, =. По таблицам находим , и согласно формуле (6.5), .

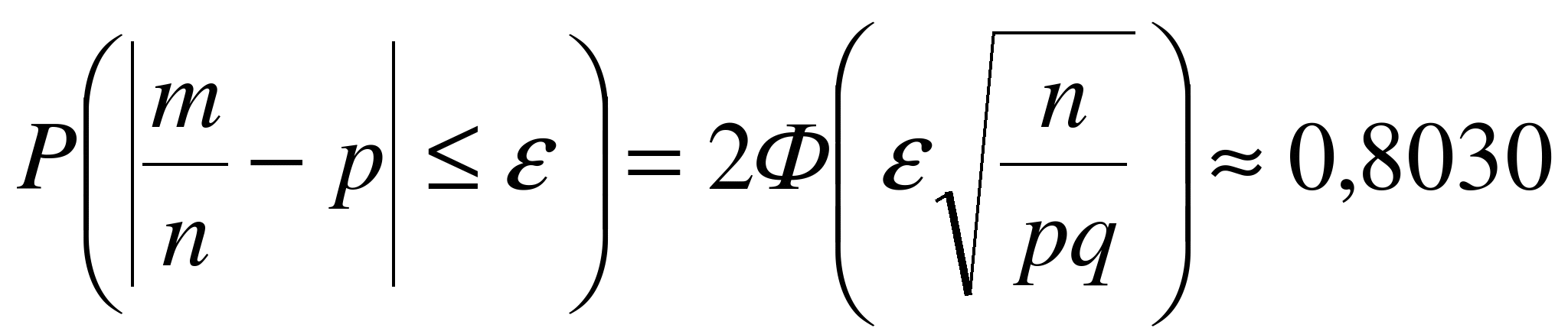Заметим, что при достаточно большом числе испытаний n и фиксированном  величина тоже велика ( при ), и 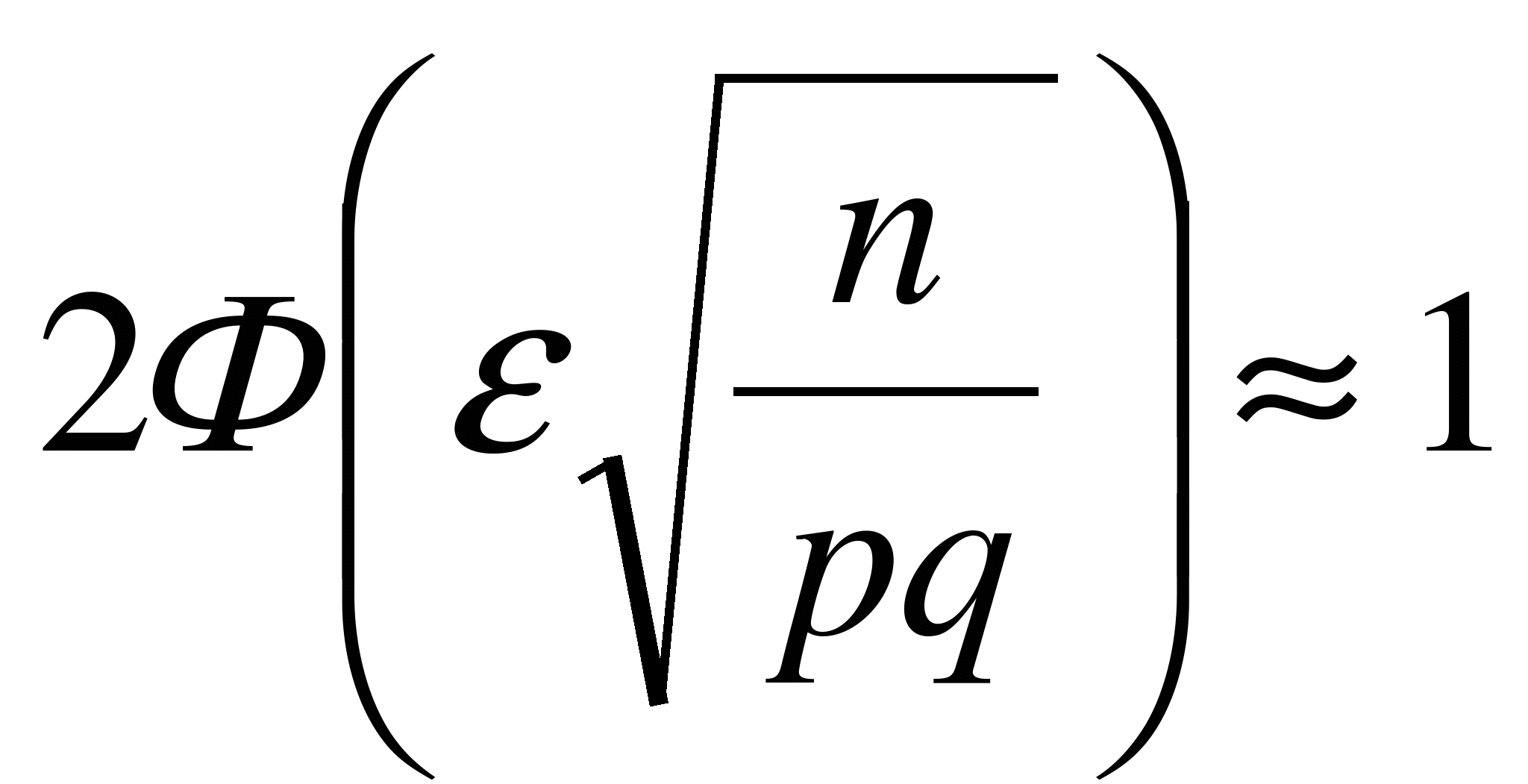(поскольку при x > 5 0,5). Это означает, согласно (6.5), что

при . (6.6)

Соотношение (6.6) носит название теоремы Бернулли. Оно показывает, что при достаточно большом числе испытаний n практически достоверным можно считать тот факт, что отклонение относительной частоты m/n (т.е. статистической вероятности) наступления события А от его вероятности p не превышает по абсолютной величине любого сколь угодно малого заданного числа .

Практически равенство (6.6) означает следующее: при большом числе испытаний n статистическая вероятность события m/n приближается к его классической вероятности p, т.е. . Подбрасывая монету достаточно большое число раз, мы вправе ожидать, что герб будет выпадать примерно в половине случаев. Бросая кубик достаточно большое число раз, можно ожидать, что шестерка выпадет в 1/6 части опытов и т.д.

В заключение параграфа приведем еще одну приближенную формулу для вычисления вероятности.

Если в условиях схемы Бернулли n достаточно велико, а , т.е. p близко к 0 или к 1, то теоремы Муавра – Лапласа уже не дают достаточной точности.

В случае, когда n велико, а p близко к 0 (т.е. событие А происходит редко), рекомендуется пользоваться приближенной формулой, полученной Пуассоном. Теорему Пуассона часто называют «формулой редких событий». Она дает хорошее приближение, если .