-
Равноускоренное движение
Движение называют равноускоренным, если оно происходит с постоянным вектором полного ускорения const. Если тангенциальная составляющая ускорения при этом не остаётся постоянной, то формулы для скорости и пути, полученные в предыдущем параграфе, не будут справедливы.
Примером такого движения может служить движение тела в однородном поле тяготения Земли или движение заряженной частицы в однородном электрическом поле плоского конденсатора.
На
рисунке 1.13 показана траектория движения
камня, брошенного под углом к горизонту
в поле тяготения Земли. Выберем оси
координат таким образом, чтобы вектор
скорости при движении тела лежал в
плоскости xy.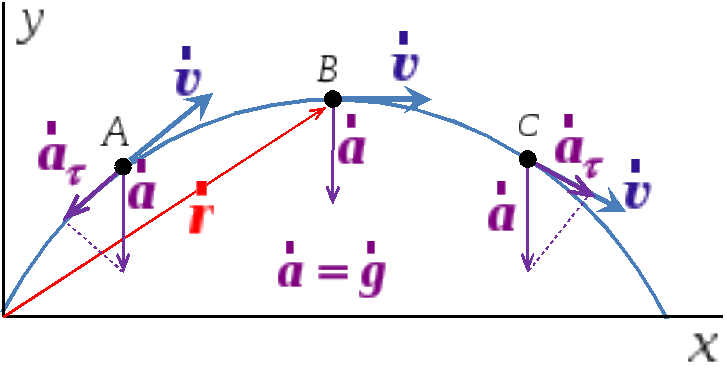 
Рис. 1.13.
Во всех точках траектории камень обладает постоянным полным ускорением , равным ускорению свободного падения , а нормальная и тангенциальная составляющие полного ускорения не остаются постоянными. В точке А векторы и направлены противоположно и . В точке В , в точке С .
Определим зависимость вектора скорости от времени наблюдения. Исходя из определения вектора полного ускорения , запишем . Интегрируя, получим:
Константу интегрирования С определим из начальных условий: пусть в начале наблюдения при t = 0 материальная точка имела скорость , тогда , а зависимость вектора скорости от времени принимает вид
Проецируя каждый вектор на оси координат, получим
,
тогда модуль скорости
Аналогично определим зависимость радиус-вектора материальной точки от времени наблюдения. Из определения вектора скорости запишем . Интегрируя, получим:
Константу интегрирования определим из начальных условий: пусть в начальный момент отсчета времени t = 0 материальная точка имела радиус-вектор , тогдa , а зависимость радиус-вектора от времени принимает вид
. (1.5)
Если в момент времени t = 0 радиус-вектор (точка начинает движение из начала координат), тогда .
Для определения положения материальной точки в любой момент времени спроецируем каждый вектор, входящий в уравнение (1.5), на оси координат:
, (1.6)
где координата есть проекция радиус-вектора на ось Ох, координата – проекция радиус-вектора на ось Оу.
При движении тела в поле силы тяжести горизонтальная составляющая полного ускорения отсутствует, горизонтальная компонента скорости постоянна (, const.), следовательно, координата х вычисляется по формуле равномерного движения: .
Вертикальная составляющая ускорения ( – ускорение свободного падения), и координата у вычисляется по формуле (1.6).
В случае прямолинейного движения радиус кривизны траектории R стремится к бесконечности, и материальная точка не обладает нормальным ускорением (). Вектор полного ускорения в этом случае представлен только тангенциальной компонентой () и направлен вдоль траектории движения. Если вектор ускорения сонаправлен с вектором скорости, то в этом случае модуль скорости возрастает, и такое движение называют прямолинейным равноускоренным движением. Если вектор ускорения имеет направление противоположное вектору скорости, то в этом случае модуль скорости убывает, и такое движение называют прямолинейным равнозамедленным движением. Так как при этом виде движения и , и , то все соотношения, выведенные в двух предыдущих параграфах, будут справедливы: