1.8.4.2. Момент инерции кольца

Вычислим моменты инерции некоторых простых тел. Найдем момент инерции однородного тонкостенного полого цилиндра (кольца) (см. рис. 1.55) массой m и радиусом R относительно перпендикулярной плоскости кольца оси симметрии. Разобьем кольцо на элементарные массы dm. По определению момент инерции . Ввиду малой толщины стенок цилиндра, можно считать, что все элементарные массы находятся на одинаковом расстоянии R от оси . То есть, r = R = const., тогда . Так как есть масса кольца, следовательно, момент инерции кольца относительно оси, перпендикулярной к его плоскости и проходящей через центр масс

Рис. 1.55

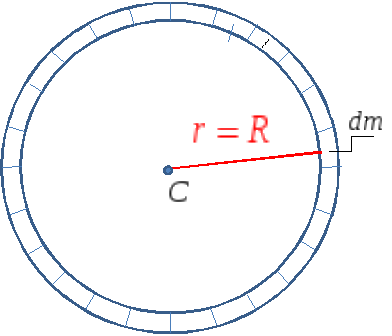
_{I = mR2.}

1.8.4.3. Момент инерции сплошного цилиндра (диска)

Найдем момент инерции однородного сплошного цилиндра массой m и радиусом R относительно его геометрической оси . Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины и радиуса . На рис. 1.56 показан только один такой цилиндр (выделен темным цветом). Момент инерции каждого полого цилиндра , где dm – масса элементарного цилиндра. Введем понятие поверхностной плотности массы цилиндра , где – площадь поверхности основания цилиндра. Тогда элементарная масса , где – площадь поверхности элементарного кольца, т. е. . Момент инерции сплошного цилиндра

.

Вынесем за знак интеграла:

Рис. 1.56

.

Учитывая, что , получим

.

То есть момент инерции однородного сплошного цилиндра массой m и радиусом R относительно его геометрической оси:

.

Для полого цилиндра момент инерции равен , где R₁ и R₂ – его внешний и внутренний радиусы.

1.8.4.4. Момент инерции однородного стержня

Найдем момент инерции тонкого однородного стержня относительно оси , проходящей через один из его концов перпендикулярно продольной геометрической оси симметрии (см. рис. 1.57). Разобьем стержень на элементарные массы dm бесконечно малой длины , удаленные от оси вращения на расстояние . Введем понятие линейной плотности массы стержня , где m – масса стержня,  – его длина, тогда элементарная масса , а момент инерции стержня будет равен

Рис. 1.57.

.

Учитывая, что , получим момент инерции однородного стержня относительно оси :

.

1.8.4.5. Теорема Штейнера

Как правило, путем интегрирования легко вычислить момент инерции I₀ симметричного тела относительно оси, проходящей через центр масс. Теорема Штейнера позволяет найти момент инерции относительно произвольной параллельной оси. Она формулируется следующим образом:

Момент инерции относительно произвольной оси вращения равен сумме момента инерции тела относительно параллельной оси вращения, проходящей через центр инерции тела, и произведения массы этого тела на квадрат расстояния между осями.

Рис. 1.58.

.

Найдем момент инерции диска относительно оси, проходящей через его край перпендикулярно плоскости диска (рис. 1.58). В этом случае a = R и, согласно теореме Штейнера,

.

Теперь рассчитаем момент инерции стержня относительно оси, проходящей через центр инерции (середину) стержня. Относительно оси, проходящей через конец стержня . Расстояние между осями (рис. 1.59). Тогда по теореме Штейнера. Отсюда .

Рис. 1.59

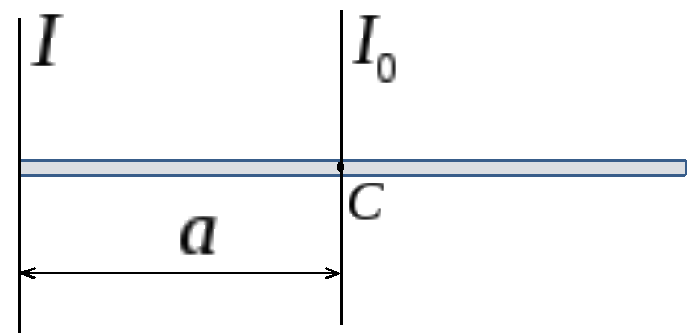
Видим, что в любом случае момент инерции тела представляется в виде I = kmr², где r – какой-либо характерный размер тела, а k – коэффициент пропорциональности, зависящий от формы тела. Единица измерения момента инерции – кг∙м².