Модуль I: основы механики

1. Механическое движение

1. Движение материальной точки

Механика – это раздел физики, изучающий простейший вид движения материи – механическое движение. Механическим движением называют перемещение тел или частей тела относительно друг друга. При описании механических движений каких-либо тел надо указывать, по отношению к каким телам рассматривается это движение, т.е. какое тело мы условно считаем неподвижным. Это тело называют телом отсчета. Для описания движения необходима система отсчёта, включающая тело отсчёта, систему координат и систему отсчета времени (часы).

Материальной точкой в физике называют тело, размеры, форма и внутренняя структура которого в данной задаче несущественны. Положение материальной точки определяется радиус-вектором , проведённым из начала координат к данной материальной точке.

Линию, вдоль которой движется материальная точка, называют траекторией движения. При движении материальной точки её радиус-вектор меняется в общем случае, как по модулю, так и по направлению. На рисунке 1.1 – радиус-вектор материальной точки в начальный момент отсчета времени.

Рис. 1.1.

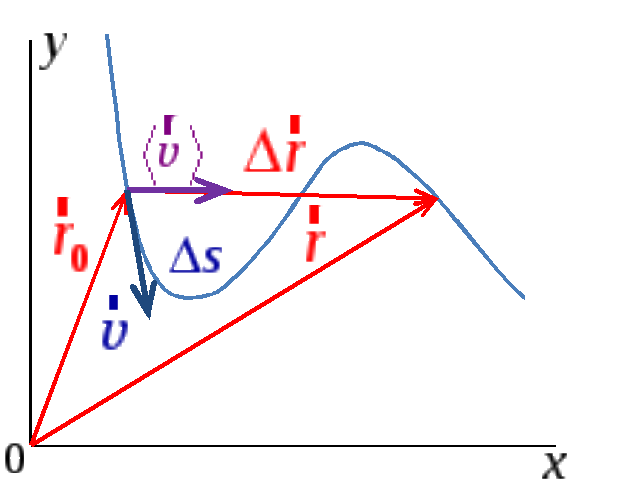
Вектор перемещенияпредставляет собой приращение радиус-вектора и соединяет положения материальной точки в начале и конце наблюдения. 

Длину участка траектории Δs называют пройденным путем. Единицей измерения пути в международной системе единиц СИ является 1 метр (м).

Модуль перемещения всегда меньше или равен пути  ∆s. Знак равенства соответствует только случаю прямолинейного движения в одном направлении. Также равенство выполняется при условии, что рассматриваемый участок траектории бесконечно мал (=ds). Такой участок принято называть элементарным.

При движении по замкнутой траектории перемещение равно нулю, чего нельзя сказать о пути.

1. Скорость

Отношение перемещения к промежутку времени, за который оно произошло, называют средним вектором скорости:

.

В тех задачах, где направление скорости не имеет значения, пользуются скалярной величиной – средним модулем скорости на данном участке

.

Иначе эту скорость называют средней путевой.

Определим вектор скорости в данный момент времени как предел отношения при t → 0. Эту скорость называют мгновенной скоростью. Мгновенная скорость равна производной радиус-вектора по времени и характеризует быстроту его изменения.

.

Вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки. Модуль мгновенной скорости:

.

Учитывая, что для бесконечно малого участка траектории , получим:

Интегрируя выражение от t₁ до t₂, найдем длину пути, пройденного точкой за промежуток времени Δt = t₂ – t₁:

Если зависимость модуля скорости от времени задать графически (рис. 1.2), то площадь заштрихованной полоски, соответствет элементарному пути: . Вся площадь под кривой v(t) соответствует пути за рассматриваемый промежуток времени Δt=t₂t₁.

2. Ускорение

Быстроту изменения вектора скорости характеризует физическая величина, называемая ускорением. Среднее ускорение равно отношению изменения вектора скорости к промежутку времени Δt, за который оно произошло.

.

Мгновенным ускорением называют физическую величину равную производной вектора скорости по времени:

Учитывая, что , получим

Определим направление и величину мгновенного ускорения материальной точки. Пусть точка движется по криволинейной траектории (рис. 1.3). Вектор скорости в любой точке траектории представим в виде: , где v – модуль скорости, а – единичный вектор, направленный по касательной к траектории в направлении движения.

Рис. 1.3.

По определению . Взяв производную произведения, получим

.

Умножим числитель и знаменатель второго слагаемого на элементарный путь ds:

.

Учитывая, что , запишем:

.

Если промежуток времени dt бесконечно мал, то все соответствующие ему точки траектории находятся на дуге окружности радиуса R, сопряженной с траекторией на данном участке. Величину R называют радиусом кривизны, а центр этой окружности – центром кривизны траектории.

Найдём разность двух единичных касательных векторов , расположенных бесконечно близко на траектории. Угол между ними также бесконечно мал. При этом угол между векторами и стремится к 90°. Нужно обратить внимание, что на рис. 1.3 это условие нарушено для наглядности чертежа. Из подобия треугольника ОАВ и треугольника, образованного векторами и (на рисунке 1.3 он покрыт точками), определим , а вектор , где – единичный вектор, перпендикулярный вектору скорости и направленный к центру окружности (центру кривизны траектории). В итоге видим, что полное ускорение выражается формулой

и состоит из двух взаимно перпендикулярных векторов: тангенциального ускорения

и нормального ускорения

Рис. 1.4.

.

Полное ускорение является суммой этих векторов (рис. 1.4):

Тангенциальная компонента ускорения направлена вдоль траектории движения в направлении скорости , если (скорость увеличивается, рис. 1.5, а) и против скорости , если (скорость уменьшается, рис. 1.5, б). Проекция вектора тангенциального ускорения на направление скорости в первом случае положительна, а во втором отрицательна.

Нормальная компонента ускорения направлена перпендикулярно касательной к траектории движения в направлении центра кривизны.

.

Рис. 1.5.

Применяя теорему Пифагора, получим модуль полного ускорения

.

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю. Если v = const., то и = 0.

Нормальная составляющая ускорения характеризует быстроту изменения вектора скорости по направлению. В случае прямолинейной траектории радиус кривизны стремится к бесконечности (R∞), значит и .

Если материальная точка движется, то ее радиус-вектор является функцией времени. Зависимость радиус-вектора движущейся материальной точки от времени называют кинематическим уравнением движения. Выберем прямоугольную декартову систему координат и запишем радиус-вектор в проекциях на оси:

,

где – координаты материальной точки, равные проекциям радиус-вектора на оси координат: , а – единичные векторы в направлении координатных осей x, y и z (орты осей). В процессе движения координаты точки меняются, т. е. являются функциями времени. Зная зависимость координат от времени, можно найти положение точки в каждый момент времени, её скорость и ускорение. Действительно, взяв производную радиус-вектора по времени, найдём вектор скорости

,

,

где – проекции вектора скорости на оси координат. Применяя теорему Пифагора, определим модуль вектора скорости

.

Аналогичным образом определим вектор мгновенного ускорения, взяв производную вектора скорости по времени

,

,

где – проекции вектора ускорения на оси координат. Модуль полного ускорения определится как

.