3. Анализ алгоритмов, реализующих метод установления

В случае решения разностной задачи Дирихле (1) параграфа 2, удается провести теоретический анализ различных алгоритмов установления с помощью конечных рядов Фурье.

3.1 Представление решения разностной двумерной задачи теплопроводности в виде конечного ряда Фурье

Рассмотрим сетку причем , М – натуральное. Совокупность вещественных функций , определенных в точках сетки и обращающихся в нуль в точках, лежащих на границе квадрата, с обычными операциями сложения и умножения их на вещественные числа, образует линейное пространство.

Введем в нем скалярное умножение

В рассматриваемом линейном пространстве размерности (М – I)² система функций

образует ортонормальный базис.

То есть .

Докажем это.

Заметим следующее:

.

Учитывая формулу получим:

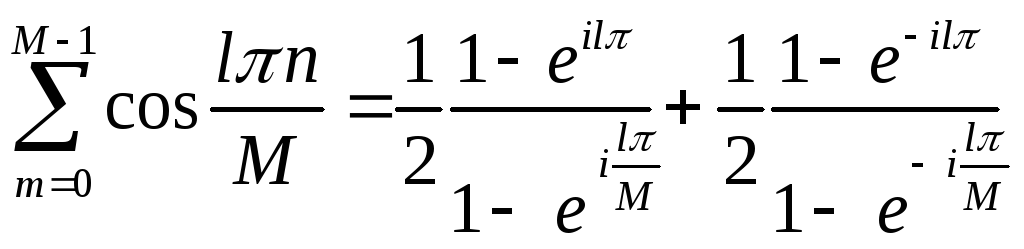
Если -четное, то числители обоих дробей равны 0.

Если -нечетное:

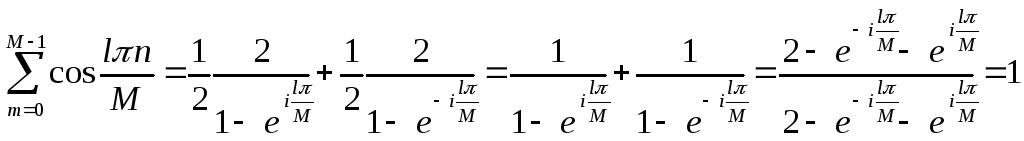
(1)

Пусть, .

Рассмотрим, как ведет себя следующее выражение:

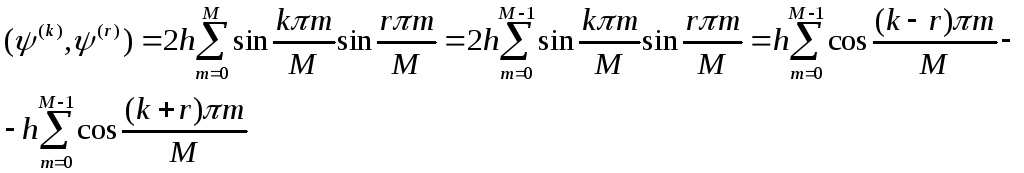(2)

Так как , то и одной четности.

Значит с учетом (1) при =0 (3)

При (4)

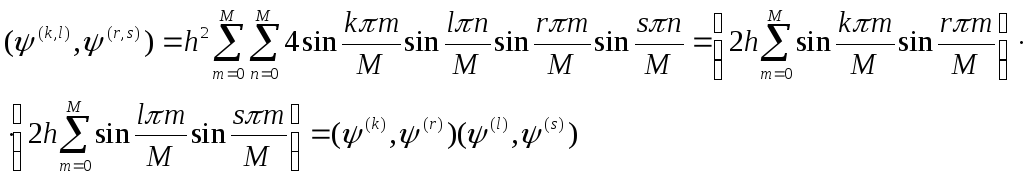
Из (3) следует, что .

Любая функция обращающаяся в нуль на границе квадрата, разлагается в конечный двумерный ряд Фурье.

,

где .

Найдем следующее выражение, которое будем использовать в дальнейшем:

, при .

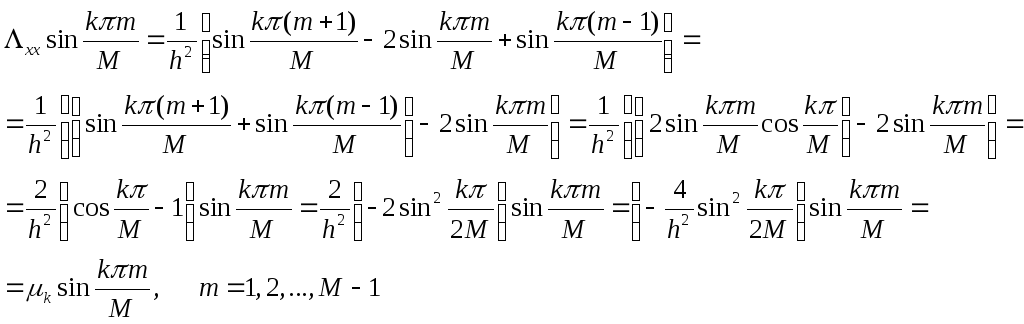(5)

Рассмотрим теперь двумерную задачу теплопроводности

, (6)

Здесь через обозначена боковая поверхность параллелепипеда .

Построим сетку , причем будем считать , где М-натуральное. За примем точки сетки, лежащие внутри и на границе параллелепипеда.

Обозначим

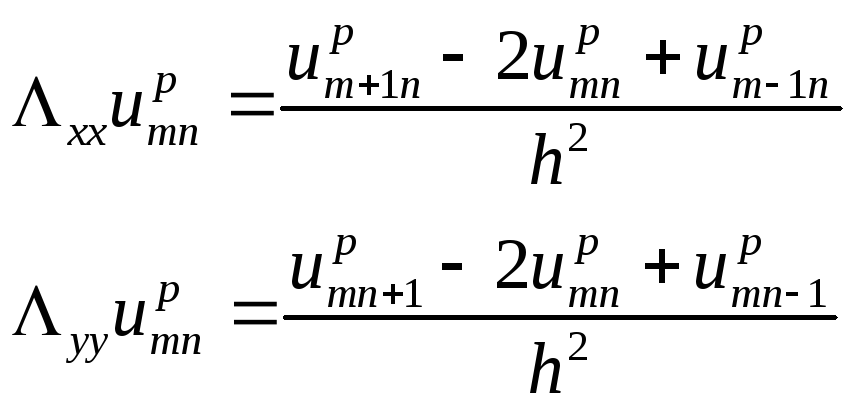
Операторы и совершенно аналогичны, только первый действует по переменному т, в то время как n и p – параметры, а второй–по переменному п, а т и р–для него параметры. Простейшая разностная схема для задачи (6) есть

(7)

Ищем решения разностного уравнения при условии вида

. (8)

Пусть , . Тогда =

Преобразуем и учитывая (5):

====

=

Тогда

= (9)

=

Подставим (8) и (9) в первое уравнение (7):

Или .

Решение (10)

удовлетворяет условиям на боковой границе при любом выборе постоянных . При это решение принимает вид .

Для того чтобы выполнялось заданное начальное условие

в качестве надо взять коэффициенты Фурье функции , т.е.

=

В силу формулы (10) коэффициентом при в разложении в ряд Фурье служит число (). Поэтому

(11)

3.2 Анализ явной схемы установления

Решение задачи (1) § 2, удовлетворяет уравнениям

+

Вычитая эти равенства из уравнений (4) § 2 почленно, получим для погрешности следующую разностную задачу:

+

0 (12)

Заметим, что сеточная функция при каждом р, р=0,1,…, обращается в нуль на границе Г. Ее можно считать элементом линейного пространства функций, определенных на сетке , и обращающихся в нуль в точках Г. Норму в этом пространстве определим, как в пункте 3.1, равенством

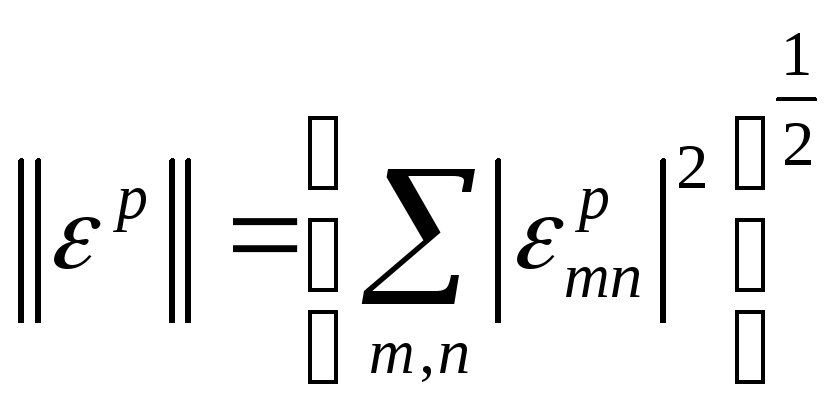
В пункте 3.1 мы получили представление для решения задачи (12) в виде конечного ряда Фурье.

где – коэффициенты разложения начальной погрешности в конечный ряд Фурье, а числа задаются формулой

=

Числа являются коэффициентами разложения погрешности в ряд Фурье по ортонормальному базису =2.

Поэтому из (11) следует

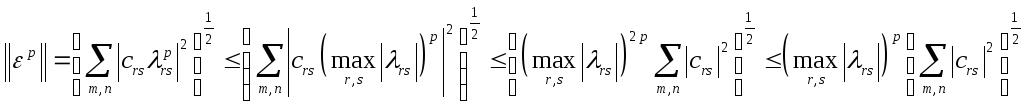
Или с учетом того, что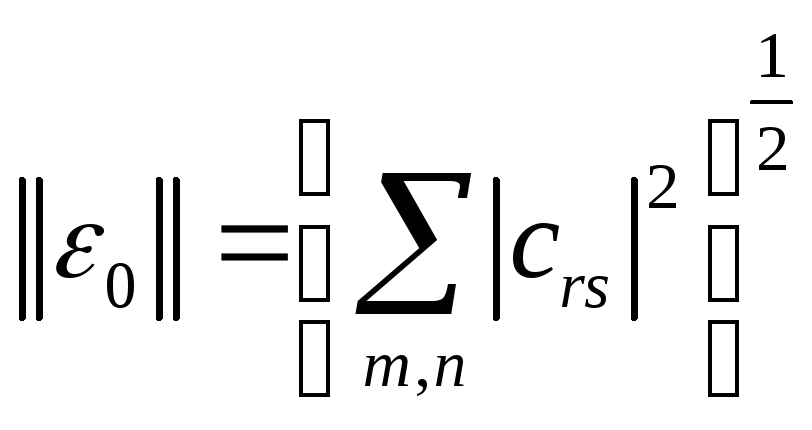, получаем .

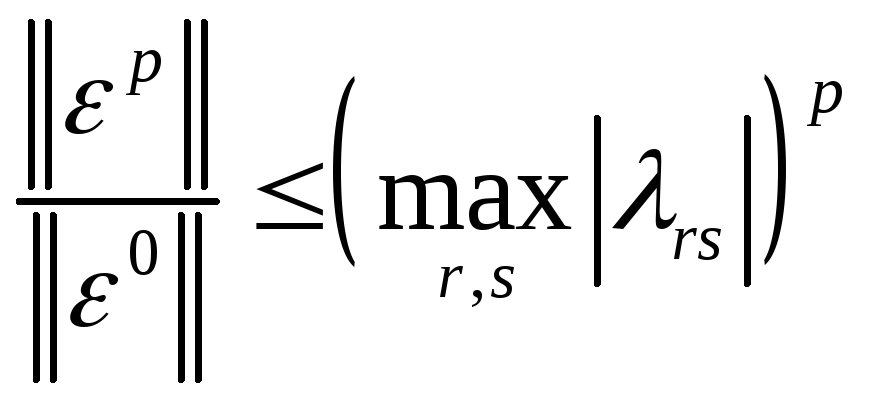Таким образом, для стремления к нулю при нужно, чтобы выполнялось неравенство

<1

Наиболее быстрое убывание погрешности получится при таком выборе , при котором принимает наименьшее возможное значение. Из формулы (11) находим самую левую и самую правую точки :

-минимальна, когда максимальна сумма , то есть при .

Самая левая точка .

-максимальна, когда минимальна сумма , то есть при .

Самая правая точка .

Увеличивая , начиная от = 0, мы вызываем сдвиг обеих этих точек влево. При том значении , при котором эти точки будут симметричны относительно точки =0, дальнейшее увеличение нецелесообразно. Действительно, при таком увеличении правая точка будет продолжать приближаться к нулю, но зато левая, которая станет больше ее по модулю, , будет удаляться от нуля.

При том , при котором , и при больших погрешность вообще не будет стремиться к нулю.

Итак, оптимальное находим из условия . При этом

=

Поэтому для уменьшения нормы первоначальной погрешности в заданное число k раз требуется проделать такое число р шагов итерационного процесса (5) § 2, чтобы

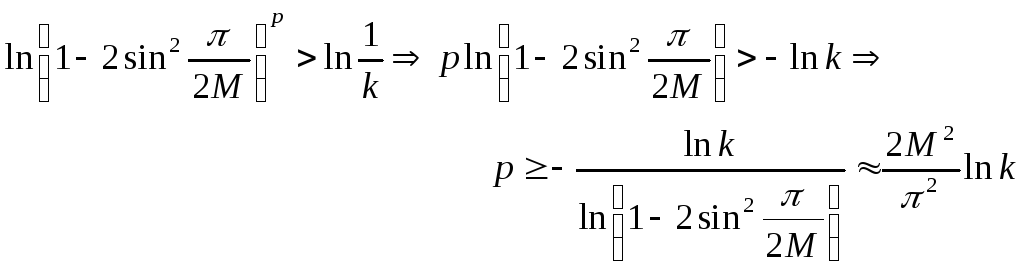
Подсчитаем число арифметических действий, необходимых для уменьшения ошибки в е раз. На каждый переход от к требуется арифметических действий. Поэтому их общее число .