
- •1. Простейшая разностная схема для задачи Дирихле
- •1.1 Построение
- •1.2 Аппроксимация
- •1.3 Устойчивость
- •Описания метода установления
- •3. Анализ алгоритмов, реализующих метод установления
- •3.1 Представление решения разностной двумерной задачи теплопроводности в виде конечного ряда Фурье
- •3.2 Анализ явной схемы установления
- •3.3 Анализ схемы переменных направлений
- •3.4 Выбор точности
Размещено на http://www.allbest.ru/
Введение
В данной работе рассмотрен метода установления для решения задачи Дирихле. В параграфе 1 исследуется аппроксимация данной задачи простейшей разностной схемой, а также устойчивость этой разностной схемы. В параграфе 2 рассмотрена идея метода установления и 2 реализующих его алгоритма для вычисления разностной задачи Дирихле.
В параграфе 3 производится анализ этих алгоритмов, использующих в первом случае явную схему установления, во втором – схему переменных направлений.
1. Простейшая разностная схема для задачи Дирихле
1.1 Построение
Задача
Дирихле для уравнения Пуассона в
квадратной области
![]() с границей Г имеет следующий вид:
с границей Г имеет следующий вид:
![]()
![]() ,
,
![]() (1)
(1)
![]()
![]()
где
функции
![]() ,
,
![]() заданы.
заданы.
Представим
задачу (1) в следующей операторной форме:
![]()
Для
этого положим
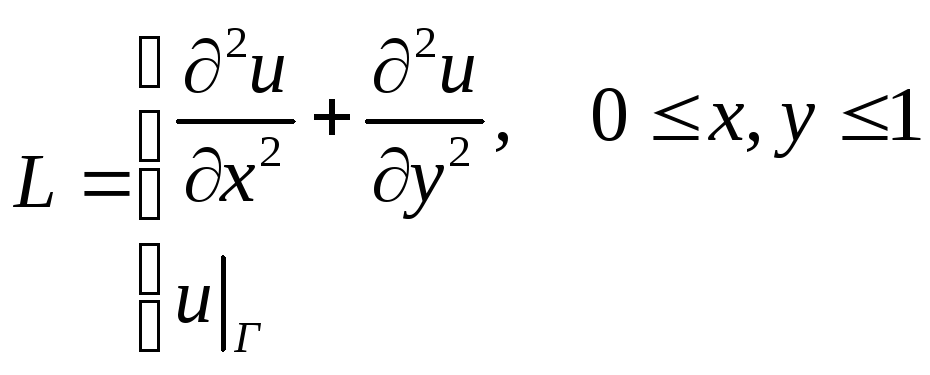 ,
,
![]() .
.
Наложим
на квадратную область
![]() квадратную сетку с шагом
квадратную сетку с шагом
![]() ,
М-целое.
,
М-целое.
Совокупность
точек
![]() сетки,
попавших внутрь квадрата или на его
границу, обозначим через
сетки,
попавших внутрь квадрата или на его
границу, обозначим через
![]() .
Точки
.
Точки
![]() ,
лежащие строго внутри квадрата
,
лежащие строго внутри квадрата
![]() ,
будем
считать внутренними точками сеточного
квадрата
,
будем
считать внутренними точками сеточного
квадрата
![]() ;
совокупность внутренних точек обозначим
;
совокупность внутренних точек обозначим
![]() .
Точки
.
Точки
![]() ,
лежащие на границе Г квадрата
,
лежащие на границе Г квадрата
![]() ,
будем считать граничными точками
сеточной области
,
будем считать граничными точками
сеточной области
![]() ;
совокупность граничных точек обозначим
;
совокупность граничных точек обозначим
![]() .
.
Для построения простейшей разностной схемы воспользуемся следующими формулами численного дифференцирования:
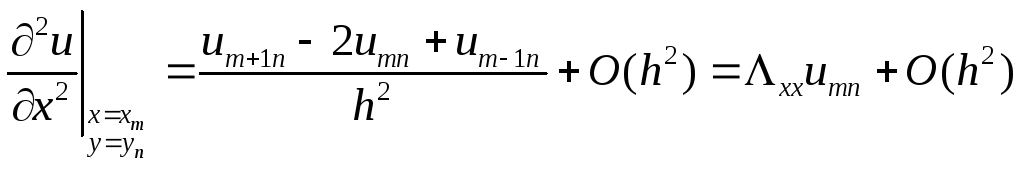 ;
;
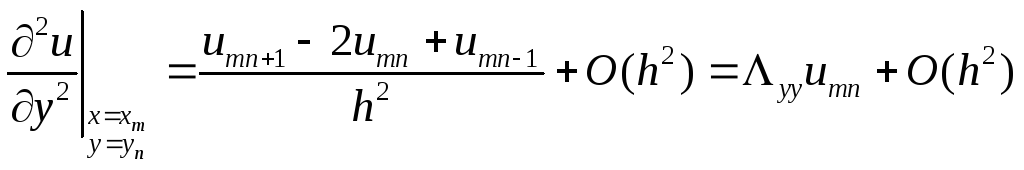 ;
;
![]()
Осуществим
замену вторых частных производных в
задаче (1) формулами численного
дифференцирования, не беря во внимание
погрешность
![]() .
.
Получим
следующую разностную схему, записываемую
в операторной форме
![]() ,
где
,
где
![]() -приблизительное
решение задачи (1):
-приблизительное
решение задачи (1):
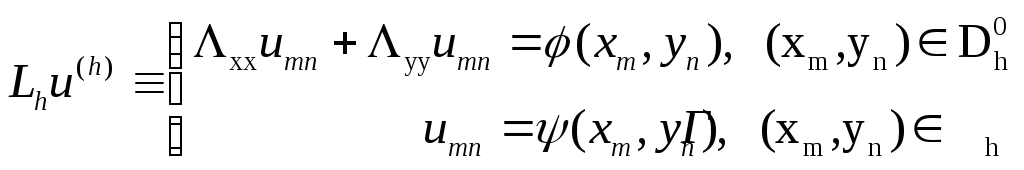 (2)
(2)
1.2 Аппроксимация
Правая
часть
![]() разностной схемы (2) имеет вид
разностной схемы (2) имеет вид
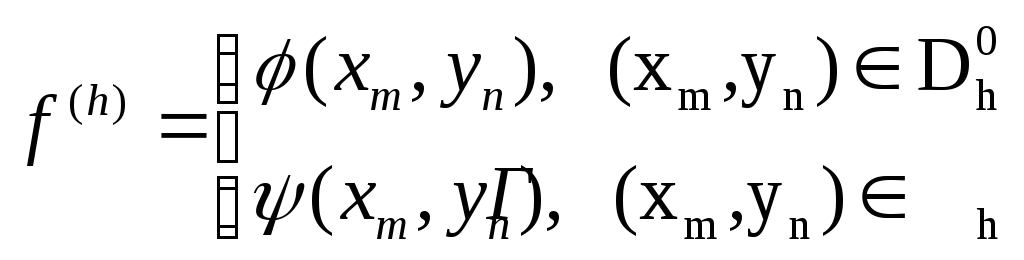 .
.
Воспользуемся формулами численного дифференцирования для установления равенства:
![]() +
+![]()
Поэтому
для решения
![]() задачи (1) имеем
задачи (1) имеем
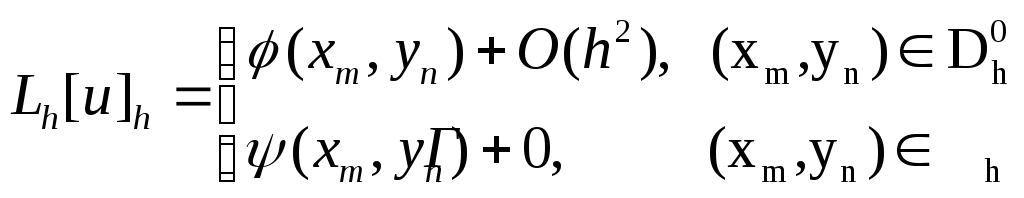 ,
где
,
где
![]() -точное
решение
-точное
решение
![]() на
сетке.
на
сетке.
Таким
образом, невязка
![]() ,
возникающая при подстановке
,
возникающая при подстановке
![]() в левую часть разностной схемы (2), имеет
вид
в левую часть разностной схемы (2), имеет
вид
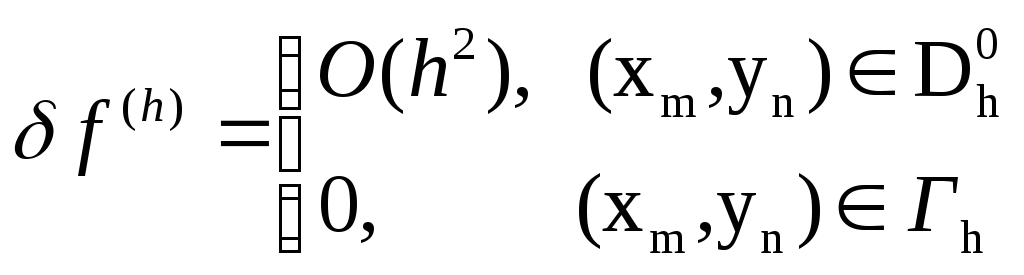
В
пространстве
![]() ,
состоящем из элементов вида
,
состоящем из элементов вида
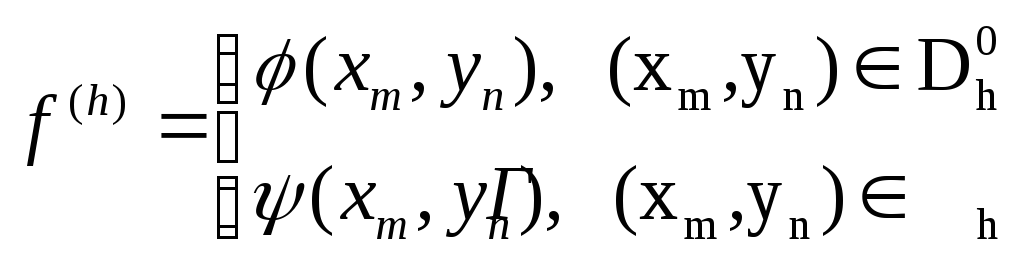 ,
,
введем
норму
![]()
![]() +
+![]()
![]() .
.
Тогда
![]() .
.
Таким
образом, разностная краевая задача (2)
аппроксимирует задачу Дирихле (1) со
вторым порядком точности относительно
h
(![]() ).
).
схема дирихле фурье установление
1.3 Устойчивость
Чтобы показать устойчивость разностной схемы (2), воспользуемся следующем ее определением:
Разностная
краевая задача
![]() устойчива, если существует
устойчива, если существует
![]() такое, что при
такое, что при
![]() и любом
и любом
![]() она однозначно разрешима,
она однозначно разрешима,
причем
![]() (с-не
зависит от
(с-не
зависит от
![]() и
и
![]() ).
).
Определим
норму в пространстве
![]() функций, заданных на сетке
функций, заданных на сетке
![]() ,
положив
,
положив
![]() .
.
Лемма
1.
Пусть функция
![]() определена
на сетке
определена
на сетке
![]() и во внутренних точках
и во внутренних точках
![]() удовлетворяет условию
удовлетворяет условию
![]()
Тогда
наибольшее на сетке
![]() значение
значение
![]() достигается хотя бы в одной точке границы
достигается хотя бы в одной точке границы
![]() .
.
Доказательство.
Допустим противное. Выберем среди точек
сетки
![]() ,
в которых
,
в которых
![]() достигает своего наибольшего значения,
какую-нибудь одну точку
достигает своего наибольшего значения,
какую-нибудь одну точку
![]() ,
имеющую самую большую абсциссу. По
нашему предположению
,
имеющую самую большую абсциссу. По
нашему предположению
![]() -
внутренняя
точка, причем
-
внутренняя
точка, причем
![]() строго
больше, чем
строго
больше, чем
![]() .
В точке
.
В точке
![]() будет
будет
![]() ,
,
поскольку первая скобка в числителе отрицательна, а остальные неположительны. Противоречие с условием.
Лемма
2.
Пусть функция
![]() определена
на сетке
определена
на сетке
![]() и во внутренних точках
и во внутренних точках
![]() удовлетворяет условию
удовлетворяет условию
![]()
Тогда
наименьшее на сетке
![]() значение
значение
![]() достигается хотя бы в одной точке границы
достигается хотя бы в одной точке границы
![]() .
.
Лемма 2 доказывается аналогично лемме 1.
Теорема (принцип максимума). Каждое решение разностного уравнения
![]()
![]()
достигает
своего наибольшего и наименьшего
значения в некоторых точках границы
![]() .
.
Доказательство получается объединением утверждений лемм 1 и 2.
Из принципа максимума следует, что задача
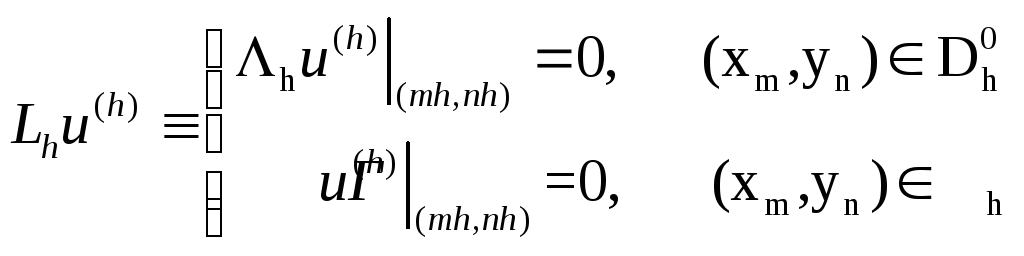
имеет
только нулевое решение
![]() ,
поскольку наибольшее и наименьшее
значения этого решения принимаются в
точках границы
,
поскольку наибольшее и наименьшее
значения этого решения принимаются в
точках границы
![]() ,
где
,
где
![]() =0.
Следовательно, определитель системы
линейных уравнений (2) отличен от нуля
и разностная краевая задача (2) однозначно
разрешима
при произвольной правой части
=0.
Следовательно, определитель системы
линейных уравнений (2) отличен от нуля
и разностная краевая задача (2) однозначно
разрешима
при произвольной правой части
![]() .
.
Переходим
к доказательству оценки
![]()
Так
как погрешность формул численного
дифференцирования
![]() для
многочленов степени
для
многочленов степени
![]() равна 0, то для произвольного многочлена
равна 0, то для произвольного многочлена
![]() второй
степени
второй
степени
![]() выполнено равенство
выполнено равенство
![]() .
.
Используя
функции
![]() и
и
![]() правой части системы (2) и фиксировав
правой части системы (2) и фиксировав
![]() ,
построим вспомогательную функцию
,
построим вспомогательную функцию
![]() ,
,
которую
будем рассматривать только в точках
сетки
![]() .
Это отражено значком h
в
обозначении
.
Это отражено значком h
в
обозначении
![]() .
В точках
.
В точках![]()
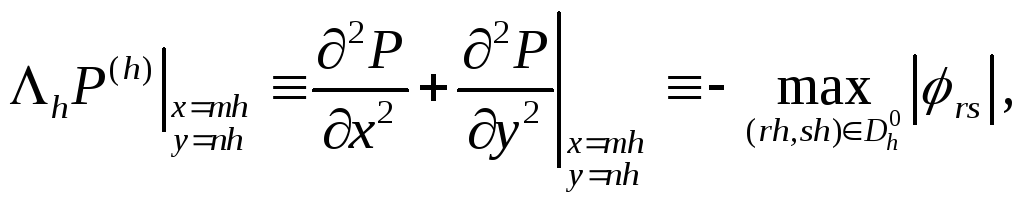
![]()
Поэтому
разность решения
![]() задачи (2) и функции
задачи (2) и функции
![]() удовлетворяет в точках
удовлетворяет в точках
![]() равенствам
равенствам
![]()
![]()
В
силу леммы 1 разность
![]() принимает свое наибольшее значение на
границе
принимает свое наибольшее значение на
границе
![]() .
Но на границе
.
Но на границе
![]() эта разность не положительна:
эта разность не положительна:
![]() ,
,
так
как в квадрате
![]() всюду
всюду
![]() и обе квадратные скобки в правой части
неположительны. Поскольку наибольшее
значение
и обе квадратные скобки в правой части
неположительны. Поскольку наибольшее
значение
![]() неположительно, то всюду на
неположительно, то всюду на
![]()
![]() или
или
![]() .
.
Аналогично,
для функции
![]() в точках
в точках
![]()
![]()
![]()
а
в точках
![]() ,
сумма
,
сумма
![]() неотрицательна:
неотрицательна:
![]()
В
силу леммы 2 всюду на
![]()
![]() или
или
![]() .
.
Таким
образом, всюду на
![]()
![]()
Отсюда вытекает неравенство, завершающее доказательство устойчивости:
![]()
![]()
![]() +
+![]()
![]() ,
где
,
где
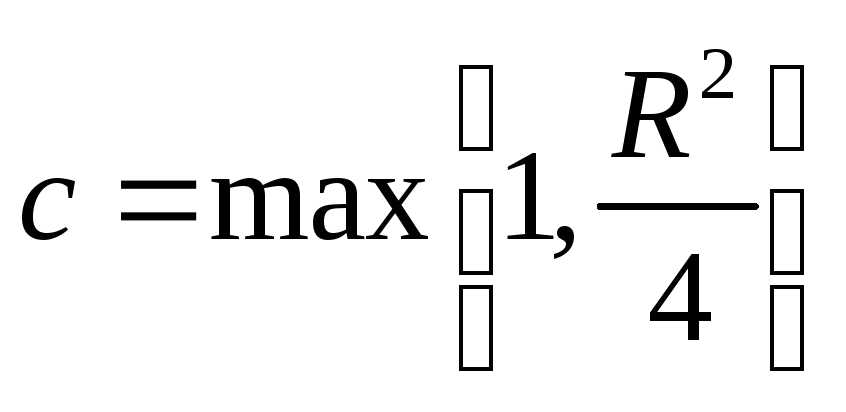 .
.
После того, как разностная краевая задача, аппроксимирующая дифференциальную, построена, нужно указать не слишком трудоемкий способ ее решения. Ведь при малом h задача (2) есть система скалярных уравнений очень высокого порядка. Одним из таких способов является использование метода установления.
