
- •Линейная алгебра.
- •5)Свойства определителя n-го порядка
- •6)Системы линейных уравнений: основные понятия
- •[Править]Пример.Система линейных уравнений:
- •Определения
- •Свойства непрерывных функций. Непрерывность сложной функции
- •Теоремы о непрерывных функциях
- •Равномерная непрерывность. Теорема Кантора
- •Монотонные функции
- •Обратная функция. Теорема о существовании обратной функции у монотонной функции
- •Непрерывность элементарных функций
- •Замечательные пределы
- •Типы неопределенных выражений
- •Определение
Замечательные пределы
Рассмотрим еще некоторые пределы, которые полезно знать.
-
Вспомним замечательный предел
![]()
Сделаем
в нем "замену переменных"
![]() .
Тогда при
.
Тогда при
![]()
![]() и
мы получим
и
мы получим
![]()
-
Вспомним, что loga – непрерывная функция. Логарифмируя предыдущее равенство, получим:
![]()
Итак,
![]()
В частности,
![]()
-
В предыдущем соотношении сделаем снова замену переменных
 .
Тогда при
.
Тогда при
 получаем
получаем
![]()
Переворачивая это соотношение, получим
![]() ,
,
В частности,
![]() .
.
-
Докажем, что
![]()
положим
![]() .
.
Тогда
при x0
y0.
Далее
![]() ,
и логарифмируя это равенство, получим
,
и логарифмируя это равенство, получим
ln(1+x)=ln(1+y)
Далее имеем
![]()
так как оба написанных предела равны 1.
-
Докажем, что при a>1 и при >0
![]()
а)
Докажем сначала, что при a>1
![]() .
Действительно, обозначим a=1+,
>0.
Пользуясь формулами
бинома Ньютона,
получим
.
Действительно, обозначим a=1+,
>0.
Пользуясь формулами
бинома Ньютона,
получим
![]() .
.
Поэтому![]() , ,
, ,
т.е.
![]() .
.![]()
б) Возьмем произвольное x+ и обозначим n=[x], т.е. целая часть от x. Тогда n x n+1 и получаем
![]() ,
,
так
что
![]() .
Поэтому
.
Поэтому
![]() .
.
в) Наконец, при произвольном >0 имеем

-
Докажем, что при >0 и a>1
![]()
Действительно, делая замену переменных loga(x)=y, x=ay, получим, что при x, y
![]()
-
Докажем, что при >0 и a>1
![]()
Действительно,
делая замену переменных
![]()
![]()
Типы неопределенных выражений
При решении различных практических задач большую роль играют так называемые неопределенные выражения или, коротко, неопределенности. Рассмотрим основные их типы.
Пусть имеются две функции u(x) и v(x).
-
Пусть
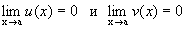 .
Тогда предел вида
.
Тогда предел вида
 называется
неопределенностью типа
называется
неопределенностью типа
 .
Процесс вычисления этого предела
называется "раскрытием неопределенности".
Разумеется, что формула
.
Процесс вычисления этого предела
называется "раскрытием неопределенности".
Разумеется, что формула
 здесь
неприменима. так как
здесь
неприменима. так как

-
Пусть
 .
Тогда предел вида
.
Тогда предел вида
 называется
неопределенностью типа
называется
неопределенностью типа .
.
-
Пусть
 .
Тогда предел вида
.
Тогда предел вида
 называется
неопределенностью типа
называется
неопределенностью типа
 .
Разумеется, и здесь нельзя пользоваться
формулой
.
Разумеется, и здесь нельзя пользоваться
формулой

Степенные неопределенности.
Рассмотрим
теперь предел вида
![]() .
.
Так
как![]() ,
то, пользуясь непрерывностью функции
ex,
можно записать
,
то, пользуясь непрерывностью функции
ex,
можно записать
![]() .
.
Это можно сформулировать в виде следующего правила: для вычисления предела выражения вида u(x)v(x) надо это выражение сначала прологарифмировать.
Какие
же неопределенности могут иметь здесь
место? Так как приходится вычислять
lim[u(x)v(x)], а здесь возможна только
неопределенность типа
![]() ,
то возможны следующие варианты.
,
то возможны следующие варианты.
-
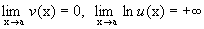 .
Последнее означает, что
.
Последнее означает, что
 и
поэтому говорят, что мы имеем дело с
неопределенностью типа
и
поэтому говорят, что мы имеем дело с
неопределенностью типа
 .
.
-
 .
Последнее означает, что
.
Последнее означает, что
 и
поэтому говорят, что мы имеем дело с
неопределенностью типа 00.
и
поэтому говорят, что мы имеем дело с
неопределенностью типа 00.
-
 .
Последнее означает, что
.
Последнее означает, что и поэтому говорят, что мы имеем дело с
неопределенностью типа 1.
и поэтому говорят, что мы имеем дело с
неопределенностью типа 1.
9) Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное
число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно
независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.
Обычно
ранг матрицы A
обозначается
![]() (
(![]() )
или
)
или
![]() .
Оба обозначения пришли к нам из
.
Оба обозначения пришли к нам из
иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского
языка, в то время как первый — для немецкого, французского и ряда других языков.
