8.6. Метод простой итерации

Допустим, необходимо уточнить корень уравнения f(x)=0 при заданном начальном приближении x₀ и необходимой точности определения корня . В методе простой итерации исходное уравнение приводят к специальному виду x=φ(x), (8.9)

который удобен для применения метода простой итерации.

Схема метода простой итерации при заданном начальном приближении x₀ имеет вид:

x_i=φ(x_i-1), (i=1,2,…,). (8.10 а)

Условие завершения итерационного процесса:

|x_k+1–x_k|<ε. (8.10 б)

Достаточным условием сходимости метода является следующее условие:

1) функция φ(x) имеет первую производную φ (x) на всей области поиска  (конечной или бесконечной),

2) для первой производной на  выполняется условие φ (x)  q <1.

Справедливость условия вытекает из следующих оценок, в которых используется теорема Лагранжа о среднем:

Так как .

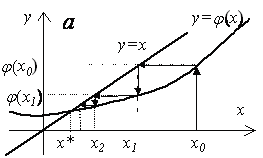
Геометрический смысл метода простой итерации.

Рис.8.3. Сходящийся метод простой итерации

Функцию, обладающую свойствами, указанными в достаточном условии сходимости, также называют для простоты сжимающим отображением. Как следует из доказательства достаточного условия сходимости, ее скорость возрастает с уменьшением параметра q<1, ограничивающего модуль первой производной φ (x).

Пример 1. Уточнить по методу простой итерации корень уравнения f(x) = cosx - 2х = 0 с точностью  = 0,01 в окрестности приближенного значения x₀ = 1 и проверить достаточное условие сходимости.

Решение. Преобразуем функцию к виду (8.9): х = (cosx)/2. Следовательно, φ(x) = (cosx)/2. Проверим достаточное условие сходимости. Так как на всей числовой оси выполняется: φ(x) = -(sinx)/2; φ (x)  1/2 <1, то итерационный процесс сходится на всей R.

Найдем искомое приближенное значение корня при x₀ = 1. Вычисления выполняем с точностью до 4 знака после запятой.

Итерация 1. х₁ = (cos(1))/2 0,2702. х₁ - х₀0,7298>.

Итерация 2. х₂ = (cos(0,2702))/2 0,4819. х₂ - х₁0,2117>.

Итерация 3. х₃ = (cos(0,4819))/2 0,4431. х₃ - х₂0,0388>.

Итерация 4. х₄ = (cos(0,4431))/2 0,4517. х₄ - х₃0,0086<.

Итерационный процесс завершаем. Ответ: х  0,4517.

Вопросы для проверки знаний.

1. К какому специальному виду приводят уравнение f(x)=0 для применения метода простой итерации ?

2. Какова схема метода простой итерации и каково условие завершения итерационного процесса ?

3. Каково достаточное условие сходимости метода простой итерации ?

4. Какой параметр определяет скорость сходимости метода простой итерации ?

Практическое задание.

1. Привести к расчетной схеме метода простой итерации, исследовать область сходимости и уточнить по методу простой итерации корень уравнения f(x) = x³ – е^х-10 = 0 с точностью  = 0,1 в окрестности приближенного значения x₀ = 20.

8.7. Метод Ньютона (метод касательных)

Для того, чтобы численно решить уравнение f(x) = 0 по методу простой итерации, его необходимо привести виду x=φ(x) (8.9), в котором функция φ(x) должна быть сжимающим отображением. Скорость сходимости максимальна, если в каждой точке x_i при выполнении итерации выполнялось бы условие φ(x_i)=0.

Если задать функцию φ(x) в виде: φ(x) = x + (x)f(x), то ее первая производная равна: φ (x)=1+ (x)  f(x) +(x)f(x). Из условия φ (x) = 0 с учетом f(x) = 0 получаем приближенную формулу для неизвестной функции (x):(x)= -1/ f(x).

При этом сжимающая функция φ(x) будет следующей: φ(x) = x - f(x)/ f(x).

Соответствующая расчетная схема итерационного процесса при заданном начальном приближении x₀ имеет вид:

x_i = x _i-1 - f(x _i-1) / f(x _i-1). (i=1,2,…) (8.11 а)

Условие завершения итерационного процесса:

|x _i –x _{i -1}| < ε. (8.11 б)

Данный метод называют методом Ньютона или методом касательных, поскольку геометрический смысл выполняемых на каждой итерации расчетов заключается в том, что действительная функция у=f(x) на каждом шаге аппроксимируется касательной, проведенной к ее графику в текущей точке x _i-1 и в качестве следующего приближения принимается точка пересечения этой касательной с осью х (рис.8.4).

Рис.8.4.Построение последовательных приближений по методу Ньютона

Последовательные приближения метода Ньютона сходятся гораздо быстрее, чем в методе простых итераций.

Пример 1. Уточнить по методу Ньютона корень уравнения f(x) = cosx - 2х = 0 с точностью  = 0,01 в окрестности приближенного значения x₀ = 1.

Решение. Так как производная функции: f(x) = -sinx – 2, то расчетная схема итерационного процесса имеет вид:

x_i = x _i-1 – (cosx _i-1 - 2x _i-1)/(-sinx _i-1– 2) = x _i-1 + (cosx _i-1 - 2x _i-1)/(sinx _i-1+ 2).

Найдем искомое приближенное значение корня при x₀ = 1. Вычисления выполняем с точностью до 4 знака после запятой.

Итерация 1. х₁ = 1+(cos1-2)/(sin1+2) = 1-1,4597/2,84150,4863. х₁ - х₀0,5137>.

Итерация 2. х₂=0,4863+(cos(0,4863)-20,4863)/(sin(0,4863)+2) = 0,4863+

(-0,0885)/2,4674  0,4504. х₂ - х₁0,0359>.

Итерация 3. х₃=0,4504+(cos(0,4504)-20,4504)/(sin(0,4504)+2) = 0,4504+

(-0,0005)/2,4353  0,4506. х₂ - х₁0,0002<.

Вопросы для проверки знаний.

1. Какова схема итерационного процесса метода Ньютона ?

2. Какова геометрическая интерпретация метода Ньютона ?

Практическое задание.

1. Уточнить по методу Ньютона корень уравнения f(x) = x³ – е^х-10 = 0 с точностью  = 0,1 в окрестности приближенного значения x₀ = 20.