Амплитудно-фазовая частотная характеристика.

Отсюда получаем так называемую амплитудно-фазовую частотную частотную характеристику звена

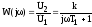Передаточная функция получается подстановкой jω=s:

Aмплитудная частотная характеристика, как и раньше,

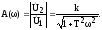
Представим амплитудно-фазовую частотную характеристику как сумму действительной и мнимой частей;

Фазовая частотная характеристика, как и раньше,

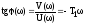При изменении частоты от =0 до = амплитудно-фазовая частотная характеристика (годограф Найквиста) - нижняя полуокружность (рис.2). При изменении частоты от =0 до =- получается верхняя полуокружность.

Обычно ограничиваются исследованием амплитудно-фазовой частотной характеристики для положительных частот, так как при <0 - получаются комплексно-сопряженные значения W(j).

Логарифмическая амплитудная частотная характеристика (лах) и

Фазовая частотная характеристика (ЛФХ).

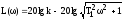Эта характеристика имеет две асимптоты. При T₁<<1 ЛАХ приближенно равна L () 20lgk так, что на интервале частот от =0 до ₁=1/T₁ логарифмическая частотная характеристика может быть заменена прямой параллельной оси абсцисс (первая асимптота).

При T₁>>1 логарифмическая частотная характеристика может быть заменена прямой с наклоном -20 дБ/дек (вторая асимптота) L()20lgk-20lg(T₁). Асимптоты пересекаются при =1/T₁=₁. Действительно, при T₁=1 L()=20lgk. Частота ₁=1/T₁называется частотой сопряжения.

Без потери общности можно положить k=1. ЛАХ для этого случая представлена на рис. 2.4. При k1 ЛАХ смещается вдоль оси L() на Lm(k).

При  = 1/T₁ полагаем Lm() = 20lgk, так, что две асимптоты сопрягаются. Частота _c=1/T₁ называется сопрягающей. В точке сопряжения разность между асимптотами и самой характеристикой максимальна и составляет 3 дБ. Этой разницей в инженерных расчетах пренебрегают. Вторая асимптота имеет наклон -20 дБ на декаду.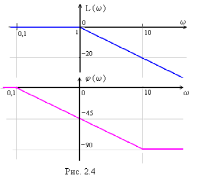

Если частоту откладывать в логарифмическом масштабе, а фазовый сдвиг в линейном, то графики зависимостей фазового сдвига от частоты

() = - arctgT₁ = - arctg(/_с)

для разных сопрягающих частот(_с ) получаются простым смещением по оси частот одной и той же кривой [2,стр.163]. Более того, как и амплитудные характеристики, логарифмические фазовые характеристики (ЛФХ) можно аппроксимировать тремя асимптотами [8]: через точку с координатами (=1/T, ()= 45 ) проводится отрезок прямой с наклоном минус 45 градусов на декаду до пересечения с прямыми ()=0 и ()=  90 (рис. 2.4). Этот отрезок аппроксимирует ЛФХ на интервале частот от =0.1T^-1 до =10T^-1 . Для <0.1T^-1 полагается ()0, а для >10T^-1 - () 90. Погрешность от такой аппроксимации не превышает 6…8 градусов.

Если k>1, то асимптота с наклоном –20 Дб/дек пересекает ось частот в точке, называемой частотой среза (_с), которая определяется из уравнения из уравнения

A() = 1, что соответствует L () = 0.

Приближенное равенство справедливо при k>>1, что обычно имеет место. Чем больше усиление k ,тем выше частота среза, тем больший диапазон частот “пропускает” звено.

Переходная функция звена (реакция на x₁(t) = 1(t))

h₁(t) = k (1-exp(-t / T₁)), t > 0,

а весовая функция (реакция на x₁(t)=(t))