3. Определение математической модели ас в виде передаточных функций

υ^* U(S) δ_в(S) ω_Z(S) υ(S)

υ(S) ω_Z(S)

Рисунок 6.

«Структурная схема АС, отвечающая преобразованной математической модели».

Произведём преобразование полученной ранее передаточной функции (1.6) .

(1.8)

-коэффициент усиления ЛА

(1.9)

_- постоянная времени;

(1.10)

_- коэффициент демфирования;

(1.11)

(1.12)

Подставив (1.9),(1.10),(1.11),(1.12) в формулу (1.8) получим

(1.13)

Найдём передаточную функцию разомкнутой системы, т.е. исходную систему необходимо привести к виду, показанному на рисунке 7

Рисунок 7.

Для того чтобы перейти к данной модели необходимо сделать ряд преобразований (рис.8, 9).

Рисунок 8.

; (1.14)

Рисунок 9.

; (1.15)

(1.16)

_, где - многочлен числителя, - многочлен знаменателя,

_,

_,

_. (1.17)

Найдем передаточную функцию замкнутой системы, тем самым преобразуем АС вида, указанного на рисунке 7, к следующему виду (рис. 10):

Рисунок 10.

(1.18)

где _,

_,

_, (1.20)

_,

_.

4. Построение частотных характеристик ас

   1. Определение корней характеристического уравнения разомкнутой системы

Используя математический пакет программ, вычислим корни характеристического уравнения вида: _.

(1.21)

Разложим многочлен знаменателя передаточной функции разомкнутой системы на множители.

(1.22)

2. Передаточная функция в виде произведения элементарных звеньев

Передаточную функцию (1.22) можно представить в виде элементарных звеньев.

- пропорциональное звено (коэффициент усиления разомкнутой системы). (1.23)

- форсирующее звено 1 порядка. (1.24)

- интегрирующее звено

- апериодическое звено 1 порядка, где

(1.25)

- апериодическое звено 1 порядка, где

. (1.26)

Определим частоту среза для каждого звена

(1.27)

Определим К_раз

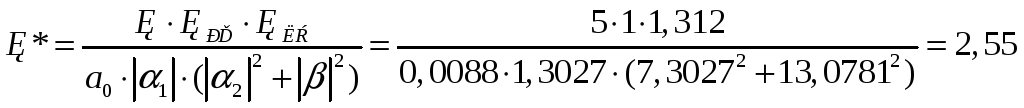(1.28).