Варианты контрольных работ для слушателей зачного отделения

Контрольная работа № 2

Вариант № 1

Задание № 1

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя):

y = a = 2; a = 3; a  .

2. Вычислить производную функций:

1). ;

2). .

3. Вычислить y' в точке x₀ :

; x₀ = 5.

4. Найти экстремумы функции:

.

5. Найти наибольшее и наименьшее значение функции y на отрезке [0, 7]:

6. Вычислить , используя правило Лопиталя:

; a = 1.

Задание № 2

1. Вычислить неопределенный интеграл

   

2. Вычислить неопределенный интеграл

3. Вычислить неопределенный интеграл .

4. Вычислить определенный интеграл

5. Вычислить определенный интеграл

6. Вычислить определенный интеграл

7. Решить дифференциальное уравнение

8. Решить задачу Коши: , .

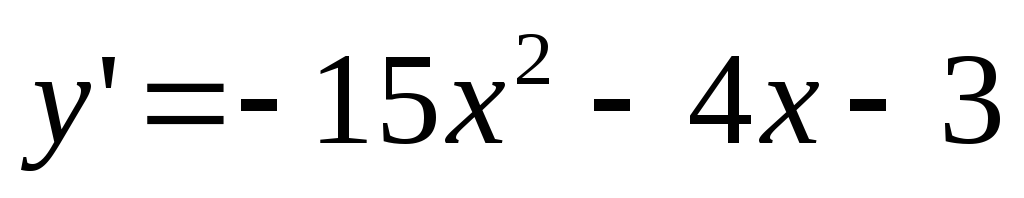1 В приведенной ниже таблице основных интегралов u может обозначать как независимую переменную, так и функцию от независимой переменной , т. е. таблица написана с учетом свойства инвариантности.

2 Выражение называется знаком двойной подстановки

3 Заметим, что в данном случае удобнее представить произвольную постоянную в виде .

23