
Задание 9.

-
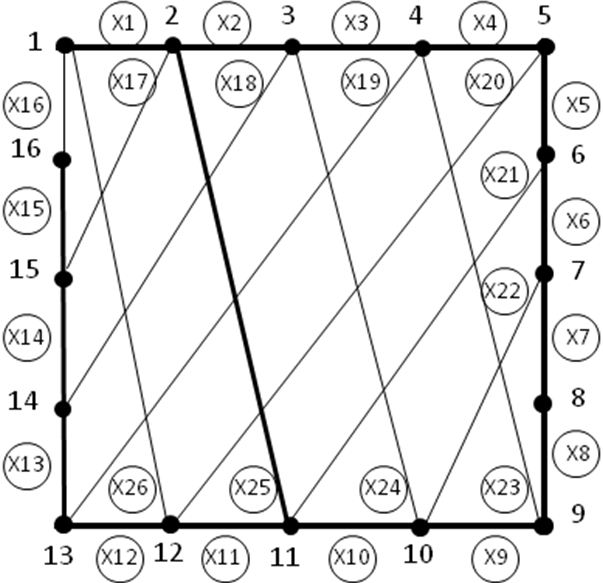
Возьмем каркас, состоящий из следующих рёбер:
{Х1,X2,X3,X4,X5,X6,X7,X8, X9,X10,X11,X12,X13,X14,X15} .

-
Рёбра, не вошедшие в каркас, являются хордами.
-
Перебираем все хорды и смотрим, образуют ли они цикл с рёбрами каркаса.
T(X16) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X16}.

T(X17) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X17}.

T(X18) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X18}.

T(X19) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X19}.

T(X20) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X20}.

T(X21) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X21}.

T(X22) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X22}.

T(X23) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X23}.

T(X24) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X24}.

T(X25) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X25}.
T(X26) = {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X26}.

-
Если перебрав все хорды, мы видим, что какие-либо хорды не вошли ни в один цикл, то они являются мостом.
-
Т.к. у нас все хорды, входят в какой либо цикл, то делаем вывод: МОСТОВ НЕТ.
Ответ: мостов нет.
Задание 14.
Найти диаметр, радиус и центры графа, заданного списком рёбер:
|
1 |
1 |
1 |
2 |
2 |
3 |
3 |
3 |
4 |
5 |
5 |
6 |
7 |
|
2 |
6 |
8 |
3 |
7 |
4 |
5 |
7 |
5 |
6 |
7 |
7 |
8 |
Постановка:
Диаметром d(G) связного графа, называется максимальное возможное расстояние между любыми двумя его вершинами.
Центром графа G называется такая вершина v, что максимальное расстояние между v и любой другой вершиной является наименьшим из всех возможных. Это расстояние называется Радиусом графа.
![]()
![]()
![]()
![]()
Центр
– вершина, где ![]() достигает минимума.
достигает минимума.
Решение.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
|
1 |
2 |
3 |
2 |
1 |
2 |
1 |
3 |
|
2 |
1 |
|
1 |
2 |
2 |
2 |
1 |
2 |
2 |
|
3 |
2 |
1 |
|
1 |
1 |
2 |
1 |
2 |
2 |
|
4 |
3 |
2 |
1 |
|
1 |
2 |
2 |
3 |
3 |
|
5 |
2 |
2 |
1 |
1 |
|
1 |
1 |
2 |
2 |
|
6 |
1 |
2 |
2 |
2 |
1 |
|
1 |
2 |
2 |
|
7 |
2 |
1 |
1 |
2 |
1 |
1 |
|
1 |
2 |
|
8 |
1 |
2 |
2 |
3 |
2 |
2 |
1 |
|
3 |

r₀(G)=
min r(c) =2
δ(G)= max r(c) =3
Ответ: радиус равен 2, диаметр равен 3, центры графа равны 2, 3, 5, 6, 7.
