Контрольные упражнения

Задания к разделу 5.1. Структура модели временной системы (5.1) при имеет вид

Рис.5.7. Структура модели объекта исследования

Операторы сопряжения между элементами смежных уровней структуры модели системы определяются алгоритмами распознавания образов

, если ; (5.20)

, если ; (5.21)

, если . (5.22)

Плотности вероятности переходов между состояниями смежных уровней структуры модели априори неизвестны и заданы выборками значений с нормальным законом распределения.

Используя датчики случайных величин с нормальным законом распределения, сформировать обучающие выборки

,

где – «указания учителя», содержащие информацию о переходе системы из -го состояния -го уровня в одно из состояний -го уровня под воздействием .

Для восстановления операторов сопряжения между состояниями смежных уровней использовать непараметрические алгоритмы распознавания образов, представленные в главе 4.

Таблица 5.9

Основные характеристики законов распределения

Решающие правила	Переходы	Математическое ожидание / среднеквадратическое отклонение
(5.20)		0/1	0/1	0/1
		2/1	2/1	2/1
(5.21)		3/1	3/1	3/1
		4/1	4/1	4/1
		6/1	6/1	6/1
(5.22)		7/1	7/1	7/1
		9/1	9/1	9/1

Условия оптимизации:

– нечёткая цель определена на состояниях -го уровня структуры модели системы

– вариант 1;

– вариант 2;

– вариант 3;

– нечёткие ограничения задаются функциями принадлежности

;

, .

Задачи исследования:

1. Разработать программное обеспечение, реализующее метод Заде – Белмана.

2. Исследовать зависимость показателя эффективности принимаемых решений от объёма обучающей выборки и количества дискретных значений 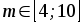управляющих воздействий.

В качестве показателя эффективности использовать

,

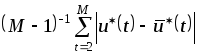где , – значения оптимальных воздействий соответственно при объёме выборки и .

Распределение вариантов задания. Студенты разбиваются на группы в соответствии с вариантами нечёткой цели. Внутри каждой подгруппы задания между студентами распределяются по значениям .

Задания к разделу 5.2. Решить задачу

в условиях, когда функции эффективности заданы выборкой наблюдений . При формировании выборок используется соотношение

,

где , – случайная величина с равномерным законом распределения.

Перед организацией вычислительного эксперимента задать параметры случайным образом из интервала .

Задания:

1. Разработать программные средства решения задачи оптимизации распределения ресурсов при неполной информации.

2. Методом вычислительного эксперимента исследовать зависимость показателей эффективности решения поставленной задачи от уровня помех и объёма обучающих выборок

,

,

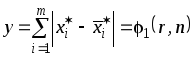где – расхождение между оптимальными решениями полученные при и .

При выполнении задания принять .

Варианты заданий формируются в соответствии с рекомендациями:

, ,

где – порядковый номер фамилии студента в списке группы.

Отметим, что разнообразие вариантов дополнительно может расширяться за счёт случайного выбора параметров функции эффективности распределения ресурсов.

Задания к разделу 5.3. На иерархическую систему обработки информации с однородной структурой поступает поток сигналов с суммарной интенсивностью . Количество уровней структуры в каждом элементе j-го уровня структуры подчинено показательному закону распределения со средним значением ( – интенсивность потока результатов обработки). Характеристики элемента -го уровня: – потери производства, связанные с задержкой обработки сигнала; – затраты в единицу времени на обслуживание технического средства; – степень разряжения входных потоков информации по сравнению с выходными.

Определить оптимальные параметры иерархической системы обработки информации с однородной структурой, при которых минимизируются экономические потери, связанные с задержкой в принятии решений и затратами на эксплуатацию системы.

При делении задания на варианты использовать различные виды плотностей вероятности (рис. 5.8).

Таблица 5.10

Характеристики элементов системы

Номер уровня структуры	Параметры элементов
1	10	0.5	6	3
2	5	1	12	7
3	3	2	20	10
4	2		40	25

Рис. 5.8. Пример видов плотности вероятности

В данных условиях необходимо:

1. Разработать программное обеспечение имитационной модели оптимизации структуры многоуровневой системы принятия решений.

2. Определить подмножество наиболее вероятных оптимальных параметров структуры многоуровневой системы обработки информации при .

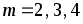3. На основе вычислительного эксперимента исследовать зависимости характеристик подмножества от количества имитаций . В качестве характеристик использовать среднее значение и количество вариантов структуры изучаемой системы.

4. Исследовать зависимость характеристик 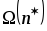от производительности вычислительных средств в узлах многоуровневой системы обработки информации .

Задания к разделу 5.4. Определить структуру вычислительной сети в виде связного графа . Количество вершин графа , а рёбер (). В каждый центр обработки информации поступает поток задач с интенсивностью , значение которых выбираются случайным образом из интервала [100, 300] с равномерным законом распределения. Интенсивность потока решений . Дисциплина обслуживания потока задач в центрах обработки информации - с отказами.

Задачи исследования:

1. Разработать программные средства, обеспечивающие оптимизацию распределения баз данных в вычислительной сети со структурой . Множество центров обработки информации, где располагаются базы данных содержит 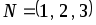элементов.

2. Исследовать зависимость суммы весов при рёбрах фрагментов кратчайших остовных графов, построенных относительно элементов множества , от производительности технических средств обработки информации в вычислительной сети. Параметр .

Формирование вариантов заданий осуществляются путём вариации количества центров обработки информации и каналов связи между ними при .

Задания к разделу 5.5. Оптимизация процесса формирования программного обеспечения системы принятия решений с линейной структурой.

Система принятия решений имеет линейную структуру (рис. 5.5). Варианты её построения и средние значения их показателей представлены в таблице 5.5. В столбце элементы необходимо поделить на 10.

Показатели вариантов являются случайными величинами с плотностями вероятностей

.

Показатель надёжности является оценкой с плотностью

.

В постановке задачи (5.18), (5.19) при =4, =3 принять , , .

Задачи исследования:

1. На основе метода МПА разработать программные средства, реализующие имитационную модель оптимизации программного обеспечения системы принятия решений с линейной структурой.

При этом использовать датчики случайных величин с заданным законом распределения, представленные в разделе 2. Параметры , интервала изменения случайных величин , принять равными

.

2. При конкретных значениях 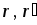исследовать зависимость среднего значения надёжности программного обеспечения от количества имитаций . Определить необходимое значение из условия устойчивости среднего значения надёжности в вычислительном эксперименте. Сравнить его со значением , рассчитанным в соответствии с неравенством Чебышева.

3. При конкретных значениях исследовать зависимость количества наиболее вероятных вариантов построения программного обеспечения, попадающих в доверительный интервал для среднего значения надёжности от числа имитаций .

Распределение вариантов среди студентов производится в соответствии с законами распределения показателей , , характеризующих варианты построения подсистем .

Дальнейшая дифференциация заданий осуществляется в зависимости от принятого количества случайных элементов в таблице характеристик вариантов построения подсистем . Будем считать, что процентное содержание элементов таблицы с интервальными значениями показателей принимает значения .