5.4. Оптимизация распределения баз данных в вычислительной сети

Вычислительная сеть является пространственно-распределённой системой, структуру которой составляют центры обработки информации и каналы связи между ними. В центры обработки информации поступают потоки задач с интенсивностью . Их технические средства обеспечивают среднее время решения одной задачи . Дисциплина обслуживания пользователей в центрах обработки информации с отказами. Если задача поступает в центр , когда все технические средства заняты решением ранее поступивших задач, то она не обслуживается. Каналы связи идентичны по надёжности.

Информация для решения задач может хранится в ограниченном множестве центров . Пусть – среднее время решения задач в вычислительной сети в условиях, когда базы данных распределены в центрах из множества . Состав баз данных достаточен для решения задач в вычислительной сети. Обозначим через затраты на поддержание баз данных.

Тогда оптимизация распределения баз данных в вычислительной сети состоит в решении задачи

(5.17)

,

где - допустимые затраты поддержания баз данных.

Методика оптимизации распределения баз данных

1. Построим модель вычислительной сети в виде графа со взвешенными рёбрами. Для компьютерного анализа графа представим его в виде матрицы смежности размерности ( – количество центров обработки информации (вершин графа)). Элементы матрицы смежности

Для идентификации модели вычислительной сети (граф ) формализуем процессы функционирования центров обработки информации с использование аппарата теории массового облуживания. В соответствии с постановкой задачи, представим центр обработки информации в виде системы массового обслуживания с отказами, которая характеризуется основным показателем эффективности – оценка вероятности отказов

,

где – приведённая интенсивность потока задач в центре . Здесь – интенсивность потока решений задач.

Рассмотрим канал между двумя центрами обработки информации . Пусть , – соответственно оценки вероятностей отказов в обслуживании задач в центрах . Тогда возможность прохождения заявки на получение информации по каналу определяется . Обозначим его значение через . С этих позиций проведём идентификацию модели вычислительной сети.

2. Определение наиболее перспективного центра обработки информации для размещения баз данных. Выберем центр обработки информации и построим относительно его кратчайший остовный граф . Известно, что кратчайший остовный граф типа «дерева» характеризуется минимальной суммой весов при рёбрах. Таким образом, вероятность прохождения заявок на получение информации для решения задач в вычислительной сети будет максимальной.

Для определения наиболее перспективного центра проведём вычислительный эксперимент относительно центров , используя метод оптимизации на графах – алгоритм «Прима».

Алгоритм «Прима» предполагает выполнение следующих действий:

1. Выбрать корневую вершину и присвоить всем остальным вершинам из большие веса , например .

2. Определить соответствие относительно вершины , которое составляет множество вершин соединённых с ребром. Множеству вершин соответствует -я строка матрицы смежности.

3. Обновить веса вершин по правилу

4. Присоединить вершину к формируемому кратчайшему остовному графу , если

.

Здесь – множество вершин, присоединённых к данному этапу строящемуся графу.

Принять , а ребро , включить в множество . На первом этапе работы алгоритма вершина соответствует минимальному значению веса при рёбрах . Пусть это будет ребро . При этом в включается ребро .

5. Перейти к этапу 2.2 заменив на и используя вместо множество .

Данный процесс продолжается до тех пор пока на некотором этапе не будет сформировано множество и множество кратчайшего остовного графа с корневой вершиной .

Обозначим через – сумму весов при рёбрах . Проведём в соответствии с алгоритмом «Прима» анализ кратчайших остовных графов для корневых вершин и выберем наиболее перспективный центр обработки информации для размещения баз данных из условия

.

Пусть этому условию соответствует корневая вершина .

Алгоритм выбора второго центра. Для определения второго перспективного центра обработки информации для размещения баз данных будем строить два кратчайших остовных графа и относительно корневых вершин и .

Графы и строятся поэтапно. Сначала право на принятие решений на этапах 2.2 – 2.4 предоставляется алгоритму «Прима» относительно корневой вершины , а затем алгоритму относительно вершины .

Данный процесс продолжается до тех пор пока между алгоритмами и не наступит конфликт. Например, по логике алгоритма вершина и ребро , ранее включены алгоритмом в строящийся граф , относится к графу . Пусть к данному – этапу работы алгоритмов , сумма весов при рёбрах построенных фрагментов графов , составляют значения , . Обозначим их сумму через .

Если вершина будет присоединена к фрагменту графа , то

,

где – вес при ребре , которое включается в фрагмент графа ; - вес при ребре , которое исключается из другого фрагмента кратчайшего остовного графа.

Тогда конфликт между алгоритмами , разрешается в пользу , т.е. вершина и ребро включается в фрагмент графа , если

либо

.

Предложенная методика разрешения конфликтов позволяет на некотором этапе построить фрагменты , графов

, ,

при которых значение критерия достигает своего минимума.

Это значит, что для обеспечения эффективности обработки информации множество центров должны получать данные из центра , а - из .

Выбор второго наиболее перспективного центра обработки информации для размещения баз данных осуществляется путём решения последовательности задач

.

По аналогии находится третий перспективный центр обработки информации. В этом случае строятся три фрагмента кратчайших остовных графов относительной , и . В процессе вычислительного эксперимента определяется новый центр обработки информации , который обеспечивает условие

.

В соответствии с постановкой задачи (5.17) отбор центров множества заканчивается, если выполняется требование .

Пример.

Выбор перспективного центра обработки информации для размещения баз данных.

Структура вычислительной сети определяется графом (рис. 5.4).

Рис. 5.4. Структура вычислительной сети

Множество допустимых центров обработки информации для распределения баз данных составляет одна вершина . Веса при ребрах графа , отражающих вероятность отказа в прохождении информации по соответствующему каналу связи, представлены в табл. 5.4.

Таблица 5.4.

Веса при рёбрах графа

Вершины графа
		0.1	0.2	0.05
			0.3			0.1
					0.25		0.1
							0.3	0.15
						0.1				0.25
											0.35
									0.2
									0.1
										0.35		0.1
											0.3	0.15
												0.1

Построим кратчайший остовный граф относительно корневой вершины , который отражает эффективный вариант передачи информации в центры её обработки из базы данных в . Для этой цели используем алгоритм «Прима», предполагающий выполнение следующих действий:

1. Присвоим веса 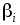=1 вершинам графа .

2. Определим соответствие относительно корневой вершины , воспользовавшись рис. 5.4 либо таблицей 5.4. Нетрудно заметить, что .

3. Обновим веса вершин . Так как начальные веса =1, то их новые значения определяются первой строкой таблицы 5.4, т.е. =0.1, =0.2, =0.05.

4. Определим минимальное значение . Таким значением является =0.05, которому соответствует вершина . Поэтому включим вершину и ребро в строящейся кратчайший остовный граф. Отметим этот факт утолщённым ребром на рисунке 5.4.

5. По аналогии с пунктами 2, 3 построим соответствие относительно вершины и обновим веса вершин . Для этого обратимся к четвёртой строке таблицы 5.4. Имеем: 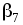=0.3, =0.15.

6. Определим новую вершину и ребро, которые присоединим к кратчайшему остовному графу из условия

.

Этому условию соответствует вершина , так как =0.1.

7. Определим и обновим их веса =0.1, а свой вес не меняет. Вес при вершине остаётся равным 0.2, так как вес при ребре равен 0.3 и больше (смотри вторую строку таблицы 5.4).

8. Найдём минимальное значение . Ему соответствует значение =0.1. На этом основании присоединим вершину и ребро к строящемуся остовному графу.

Продолжая реализацию предложенной методики получим кратчайший остовный граф (рис. 5.4). При этом последовательно будут присоединяться к строящемуся кратчайшему остовному графу вершины , , , , , , , . Кратчайшему остовному графу соответствует подграф на рисунке 5.4 с утолщёнными рёбрами.