
- •4.1. Синтез байесовских решающих функций
- •4.2. Непараметрические оценки решающих функций
- •4.3. Непараметрические алгоритмы распознавания образов коллективного типа
- •4.4. Синтез и анализ непараметрического решающего правила, основанного на оценках плотностей вероятности
- •4.5. Частотные алгоритмы распознавания образов в пространстве дискретных признаков
- •4.6. Непараметрический алгоритм классификации, основанный на частотном методе распознавания образов
- •4.7. Многоуровневые системы распознавания образов
- •4.8. Непараметрические алгоритмы распознавания образов с учётом взаимосвязи между признаками
- •4.9. Нелинейные непараметрические коллективы решающих правил в задачах распознавания образов
- •4.11. Непараметрические алгоритмы распознавания образов, основанные на рандомизированном методе их идентификации
- •4.12. Непараметрические алгоритмы классификации множеств случайных величин
- •Литература
- •Дополнительная литература
- •Контрольные вопросы
- •Контрольные упражнения
4.12. Непараметрические алгоритмы классификации множеств случайных величин
Пусть имеется
обучающая выборка
![]() ,
составленная из множеств
,
составленная из множеств
![]() независимых наблюдений признаков
независимых наблюдений признаков
![]() классифицируемых объектов и «указаний
учителя» об их принадлежности к одному,
например, из двух классов
классифицируемых объектов и «указаний
учителя» об их принадлежности к одному,
например, из двух классов
![]() .
.
Законы распределения
![]() неизвестны и характеризуются наблюдениями
неизвестны и характеризуются наблюдениями
![]() .
.
Подобные условия встречаются при исследовании объектов, параметры которых многократно измеряются в течении короткого интервала времени; при оценивании качества партии изделий по случайно выбранному их ограниченному набору; при обработке больших массивов статистических данных.
Идея предлагаемого подхода заключается в замене операций над множествами на менее трудоемкие и хорошо разработанные операции над функциями либо над их параметрами, используя методы локальной аппроксимации.
С этих позиций непараметрическое решающее правило классификации в двуальтернативной задаче распознавания образов представляется в виде

где уравнение разделяющей поверхности
 (4.45)
(4.45)
восстанавливается
по обучающей выборке
![]() объёма
объёма
![]() ,
где
,
где
![]() - оценки функций
распределения ;
- оценки функций
распределения ;

- «указания учителя».
В качестве критерия
близости между оценками функций
распределения
![]() и
и
![]() используется, например, ядерная мера
используется, например, ядерная мера

Предложенная мера
близости основана на использовании
критерия Смирнова для проверки гипотезы
![]() с уровнем доверия
с уровнем доверия
![]()
![]() ,
,
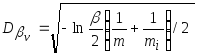 ,
,
где
![]() ,
,
![]() - соответственно количество элементов
множества
- соответственно количество элементов
множества
![]() и
и
![]() .
.
Превышение
порогового значения
![]() критерия Смирнова означает нарушение
гипотезы
критерия Смирнова означает нарушение
гипотезы
![]() .
.
Выбор оптимальных
![]() осуществляется в режиме «скользящего
экзамена» из условия минимума эмпирической
ошибки распознавания образов
осуществляется в режиме «скользящего
экзамена» из условия минимума эмпирической
ошибки распознавания образов
 ,
,
где индикаторная функция

Литература
-
Лапко, А.В., Ченцов С.В., Крохов С.И., Фельдман Л.А. Обучающиеся системы обработки информации и принятия решений. - Новосибирск: Наука, 1996 - 296с.
-
Лапко А.В., Ченцов С.В. Многоуровневые системы принятия решений. - Новосибирск: Наука, 1997. – 190 с.
-
Лапко А.В., Ченцов С.В. Непараметрические системы обработки информации: Учебное пособие. – М.: Наука, 2000. – 350 с.
-
Лапко А.В., Лапко В.А., Соколов М.И., Ченцов С.В. Непараметрические системы классификации. - Новосибирск: Наука, 2000. – 240 с.
-
Лапко В.А., Соколов М.И. Непараметрические методы обработки данных: Учеб. пособие. – Красноярск: ИПЦ КГТУ, 2001. – 116 с.
-
Лапко В.А. Непараметрические коллективы решающих правил. - Новосибирск: Наука, 2002 – 168 с.
-
Лапко В.А. Компьютерное моделирование систем и статистический анализ данных: Методические указания для выполнения лабораторных работ. – Красноярск: ИПУ КГТУ, 2006. – 48 с.
-
Лапко В.А. Теория принятия решений. Непараметрические модели восстановления стохастических зависимостей и распознавания образов: Методические указания для выполнения лабораторных работ. – Красноярск: ИПУ КГТУ, 2006. – 27 с.
-
Лапко А.В., Лапко В.А. Непараметрические системы обработки неоднородной информации. – Новосибирск: Наука, 2007. – 174 с.
