Глава 4.

статистические МЕТОДЫ РАСПОЗНАВАНИЯ ОБРАЗОВ

Основное внимание в данной главе уделяется проблемам синтеза и анализа алгоритмов распознавания образов в условиях неполной информации о вероятностных характеристиках классов. Для преодоления априорной неопределённости используются непараметрические оценки условных плотностей вероятности распределении признаков сигналов о состоянии классифицируемых объектов. Сигналом называют вектор входных переменных . Получаемые при этом алгоритмы распознавания образов являются непараметрическими. С учётом специфики непараметрических алгоритмов распознавания образов рассматриваются вопросы их оптимизации, оценки эффективности и минимизации описания как путём формирования наборов информативных признаков сигнала, так и с позиций алгоритмического подхода.

4.1. Синтез байесовских решающих функций

Рассмотрим объект (рис. 4.1) с входом , который может быть вектором , и выходом – скаляр. Выходная переменная является дискретной случайной величиной.

Рис. 4.1. Объект исследования.

Существует некоторая неизвестная зависимость между входом и выходом . Необходимо оценить данную зависимость, построив модель .

Пусть дана выборка статистически независимых наблюдений случайной величины , распределённых с неизвестной плотностью , где – «указания учителя» о принадлежности ситуации к тому либо иному классу .

Под классом понимается совокупность наблюдений, связанных между собой каким либо свойством или целью.

Необходимо построить решающее правило , позволяющее в автоматизированном режиме принимать решение о принадлежности новых ситуаций к классам .

При наличии двух классов (рис. 1) принимает значения и . Если классифицируемые объекты характеризуются двумя признаками, то двуальтернативная задача распознавания образов иллюстрируется рис. 4.2, где – разделяющая поверхность (решающая функция) между классами и .

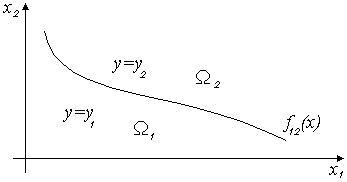
Рис. 4.2. Задача распознавания образов в двухмерном случае

Для последующего анализа построим плотности вероятности классов в одномерном случае (рис. 4.3).

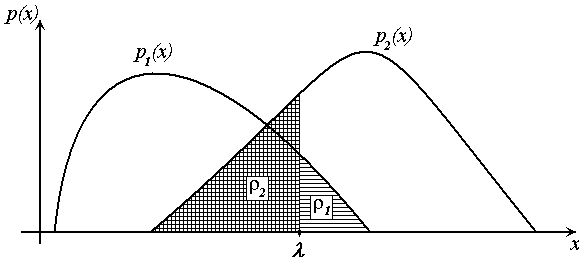
Рис. 4.3. Задача распознавания образов в одномерном случае

Определим некоторую границу на оси и запишем решающее правило

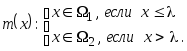
Тогда ошибка распознавания первого класса составит

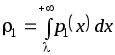
и для второго класса

.

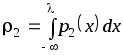Общая ошибка распознавания, например, при равенстве априорных вероятностей классов

.

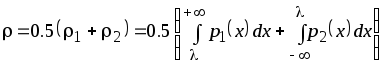Для определения наилучшей границы найдём минимум суммарной ошибки по параметру

.

Возьмём производную полученного критерия по параметру и приравниваем к нулю. Производная от интеграла соответствует значению подынтегрального выражения в точке

.

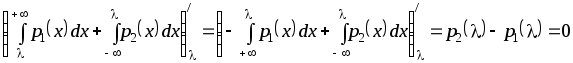В итоге получаем

.

Оптимальная граница находится в точке пересечения двух классов. Полученная разделяющая поверхность между классами называется байесовской решающей функцией и имеет вид

. (4.1)

Исходя из этого, решающее правило будет иметь вид:

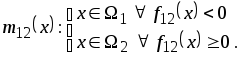
Решающее правило, соответствующее данной байесовской разделяющей поверхности, называется правилом максимального правдоподобия.

Далее рассмотрим ситуацию когда, априорные вероятности классов разные. Пусть – общее количество наблюдений; – количество наблюдений первого класса; – количество наблюдений второго класса.

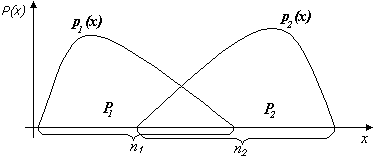
Рис. 4.4. Задача распознавания образов для случая

Тогда частота появления точек первого и второго класса будет соответствовать

.

Поэтому, если , то ошибка распознавания второго класса будет больше, т.к. точки второго класса появляются в области пересечения классов чаще.

Ошибка для первого класса определяется выражением

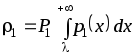
и для второго класса

.

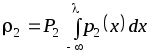Исходя из этого, запишем суммарную ошибку

.

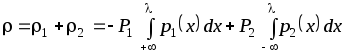Найдём минимум суммарной ошибки по границе и получим байесовскую разделяющую поверхность

. (4.2)

Тогда решающее правило, соответствующее данной разделяющей поверхности, будет иметь вид

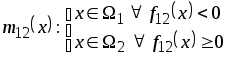
и называется правилом максимума апостериорной вероятности.