
- •Линейные волны
- •Волновое уравнение. Бегущие волны
- •Преобразование Фурье.
- •Монохроматическая волна.
- •Характеристики линейных волн.
- •Фазовая скорость линейных волн
- •Дисперсия среды. Групповая скорость линейных волн
- •Явление опрокидывания (укручения) нелинейных волн
- •Преобразование Коула – Хопфа. Ударные волны
- •Асимптотические решения уравнения Бюргерса. Ширина фронта ударной волны
- •Оценки ширины фронта ударной волны. Число Рейнольдса
- •Спектр ударной волны.
- •Солитоны
- •Стационарные волны
- •Солитонные решения волнового уравнения (общие свойства)
- •Солитонное решение уравнения Кортевега - де -Вриза
- •Решение уравнения КдВ (общий вид)
- •Законы сохранения
- •Нелинейные уравнения, обладающие солитонными решениями
- •Нелинейные уравнения, не имеющие решений в виде солитонов.
- •Динамический хаос
- •Нелинейный маятник
- •Характеристики нелинейного маятника.
- •Особенности движения вблизи сепаратрисы
- •Переменные: «Действие» и «угол»
- •Уравнение нелинейного маятника при наличии внешней периодической силы.
- •Перекрытие резонансов. Критерий стохастичности
- •Параметрический резонанс
-
Явление опрокидывания (укручения) нелинейных волн
А.Вывод эквивалентного уравнения
Рассмотрим
уравнение Кортевега-де-Вриза (КВД):
(приняв
![]() )
)
![]() .
.
Чтобы выделить явление
нелинейности, будем пренебрегать
дисперсией среды:
![]() (т.е.
отбросим
(т.е.
отбросим
![]() )
)
Уравнение перепишется:
![]()
Начальное возмущение:
![]() .
(*)
.
(*)
Скорость распространения
волны:
![]()
![]() (1)
(1)
Известно, что если
![]() ,
то решение будет
,
то решение будет
![]() .
.
Пусть решение (1):
![]() (2)
(2)
Выражение (2) является функциональным уравнением, эквивалентным уравнению (1).
Покажем, что решения (1) и (2) совпадают.
Возьмем производные
и обозначим:

![]()
![]()
Подставим в (1)
![]()
![]() =>
=>
![]() ч.т.д.
ч.т.д.
Б. Укручение волн
Явление укручения волн рассм. на основе эквивалентного функционального уравнения (2).
Пусть начальный импульс волны имеет треугольный вид:


Кусочно-линейная функция, описывающая начальное возмущение в форме треугольника.
Эта форма начального импульса является достаточно хорошим приближением реального импульса более общей горбовидной формы.
Учтем:
![]()
Используем функциональное уравнение (2):

Введем новую переменную
![]() ,
тогда:
,
тогда:
![]()

На основе функционального уравнения (2):

Возьмем производную:
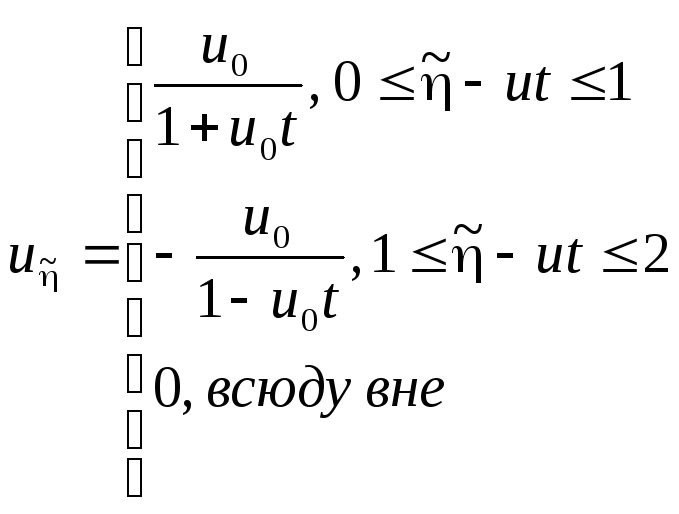
u0
Это явление и называют укручением волны.
![]() в
точке
в
точке
![]() ,
импульс имеет прямоугольную форму.
,
импульс имеет прямоугольную форму.
При
![]() производная
производная
![]() правой
стороны импульса становится положительной,
импульс принимает форму при t3.
правой
стороны импульса становится положительной,
импульс принимает форму при t3.
![]() - безразмерное время
(нормированное на
- безразмерное время
(нормированное на
![]() )
)
Импульс меняет формы
В последнем промежутке появляется неоднозначность функции.
Если волновой процесс (например, описывает колебание плотности среды), то в данной точке пространства значение u будет разным (2 значения), а т.к. u описывает при этом плотность вещества, то в заданной точке пространства мы будем иметь разную плотность вещества.
Этот результата получается из-за того, что при t = tкр происходит разрушение волны.
Обратимся к соотношениям (3).


Если
![]() ,
то исходная функция однородная, то она
будет константой и дальше.
,
то исходная функция однородная, то она
будет константой и дальше.
![]()
![]() означает
неоднородность начального профиля
волны.
означает
неоднородность начального профиля
волны.
![]() ,
то скорость зависит от u.
=> волна нелинейная.
,
то скорость зависит от u.
=> волна нелинейная.
tкр определяет время разрушения волны:
 укручение волны.
укручение волны.
![]()
![]()

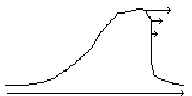

t0 x t1 x t2 x
Замечания:
В действительности, не всегда возникает разрушение нелинейной волны. Процессу опрокидывания и разрушения волны препятствуют два явления: диссипация (затухание волн в среде) и дисперсия.
Диссипация и дисперсия являются конкурирующими процессами с нелинейностью.
В результате этой конкуренции опрокидывание волны не происходит, и устанавливаются ударные волны.
-
Преобразование Коула – Хопфа. Ударные волны
Рассмотрим влияние рассеяния (затухания) на явление укручения волн.
Пусть имеется уравнение Бюргерса
![]() , (1)
, (1)
![]() - коэффициент диффузии.
- коэффициент диффузии.
Свойство уравнения Бюргерса состоит в том, что его можно свести к линейному уравнению теплопроводности. Для этого нужно провести преобразование Коула-Хопфа^
![]() - (2), где
- (2), где
![]() =const .
=const .
Данная замена определяет
функцию F
с точностью до времени.
![]() .
.
Найдем производные:
![]()


Подставляем
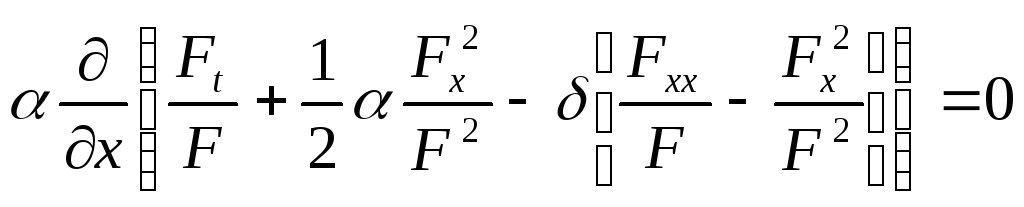
Выберем
![]() (тогда нелинейные слагаемые уйдут)
(тогда нелинейные слагаемые уйдут)
![]()
Проинтегрируем
![]()
![]() ,
,
т к F(x,
t)
определяется с точностью до функции
времени, то c(t)
берут равной нулю.
![]() .
.
(При F=0
имеем тривиальное решение). Т к
![]() ,
то можно записать:
,
то можно записать:
![]() – уравнение
теплопроводности.
– уравнение
теплопроводности.
Решение:
![]()
Необходимо определить
![]() .
Зададим начальный импульс
.
Зададим начальный импульс
![]() .
.
Предположим, что
интеграл ограничен :
![]() .
.
Из преобразования Коула –Хопфа:
![]()

Подставляем, получаем решение

Введем функцию
![]()
![]()
Подставляем в (2) и получим решение уравнения Бюргерса

 (10)
(10)
Решение (10) позволяет получить решения в общем виде для уравнения Бюргерса, соответствующие различным начальным профилям волны.
