
- •Линейные волны
- •Волновое уравнение. Бегущие волны
- •Преобразование Фурье.
- •Монохроматическая волна.
- •Характеристики линейных волн.
- •Фазовая скорость линейных волн
- •Дисперсия среды. Групповая скорость линейных волн
- •Явление опрокидывания (укручения) нелинейных волн
- •Преобразование Коула – Хопфа. Ударные волны
- •Асимптотические решения уравнения Бюргерса. Ширина фронта ударной волны
- •Оценки ширины фронта ударной волны. Число Рейнольдса
- •Спектр ударной волны.
- •Солитоны
- •Стационарные волны
- •Солитонные решения волнового уравнения (общие свойства)
- •Солитонное решение уравнения Кортевега - де -Вриза
- •Решение уравнения КдВ (общий вид)
- •Законы сохранения
- •Нелинейные уравнения, обладающие солитонными решениями
- •Нелинейные уравнения, не имеющие решений в виде солитонов.
- •Динамический хаос
- •Нелинейный маятник
- •Характеристики нелинейного маятника.
- •Особенности движения вблизи сепаратрисы
- •Переменные: «Действие» и «угол»
- •Уравнение нелинейного маятника при наличии внешней периодической силы.
- •Перекрытие резонансов. Критерий стохастичности
- •Параметрический резонанс
-
Линейные волны
-
Волновое уравнение. Бегущие волны
-
Пусть U – n-мерный вектор, описывающий некоторый волновой процесс и являющийся функцией координаты и времени. Тогда его эволюцию описывает волновое уравнение Даламбера:
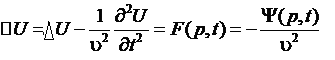 (1)
(1)
![]() -
n-мерный
оператор Лапласа, F(Р,t)
– правая часть, некоторая функция,
зависящая от координаты т. Р в пространстве
и времени t
, v
(
-
n-мерный
оператор Лапласа, F(Р,t)
– правая часть, некоторая функция,
зависящая от координаты т. Р в пространстве
и времени t
, v
(![]() >0
)– скорость;
>0
)– скорость;
Начальные условия:
 (2)
(2)
Если
![]() = const
(не зависит от U),
то уравнение линейное.
= const
(не зависит от U),
то уравнение линейное.
Р ассмотрим
одномерное уравнение U(x,t)
= 0, т.е.
ассмотрим
одномерное уравнение U(x,t)
= 0, т.е.
 . (3)
. (3)
Можно привести примеры волновых процессов, описываемых данным уравнением:
-
колебания бесконечной струны, тогда: U(x,t) – отклонение от положения равновесия,
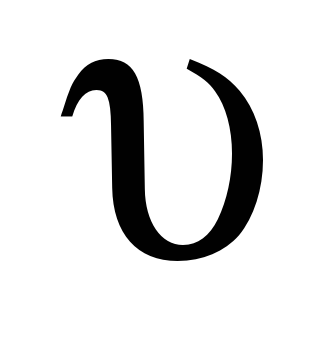 - скорость распространения сигнала по
струне
- скорость распространения сигнала по
струне
 ,
,
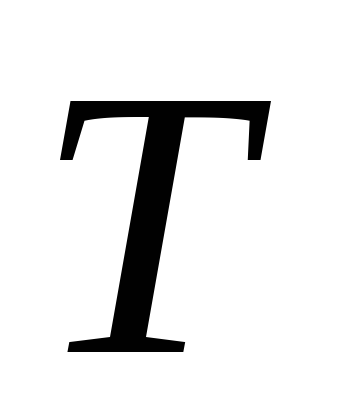 - натяжение струны,
- натяжение струны,
 - линейная плотность,
- линейная плотность, -
Электромагнитные колебания,
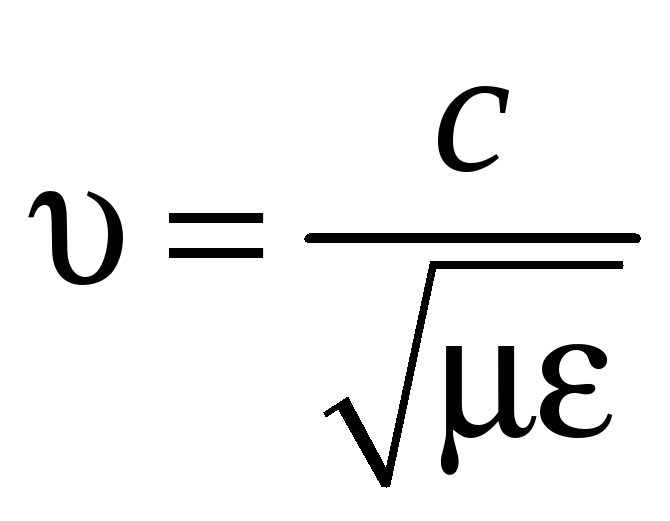 .
(Для воздуха и вакуума
.
(Для воздуха и вакуума
 )
)
Метод Даламбера:
Уравнение характеристик:
![]() . (3.1)
. (3.1)
Интегрируем, Введем новые переменные:
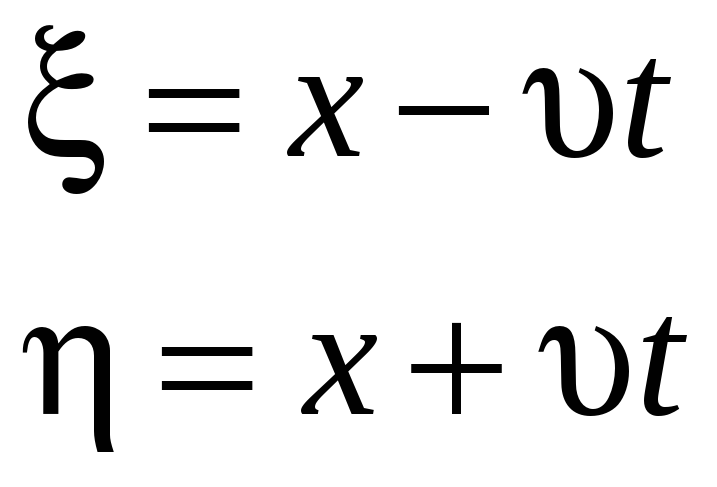 ,
-характеристики (решения (3.1))
,
-характеристики (решения (3.1))
тогда решением уравнения
(3) будет любая дважды дифференцируемая
функция от
![]() и
и
![]() :
F(
:
F(![]() ,
,![]() ).
).
Общее решение:
![]() ,
(4)
,
(4)
где
![]() - описывает расходящуюся волну от
источника (расходящаяся
волна),
- описывает расходящуюся волну от
источника (расходящаяся
волна),
![]() - описывает волну, приходящую в некоторую
область (сходящаяся
волна).
- описывает волну, приходящую в некоторую
область (сходящаяся
волна).
Решение (4) называется решением в виде бегущих волн.
 v-фазовая
скорость волны.
v-фазовая
скорость волны.
-
Преобразование Фурье.
Пусть U(x,t) –некоторый волновой импульс.
В линейном случае его можно представить в виде преобразование Фурье:
 ,
где (5)
,
где (5)
Фундаментальное решение уравнения будет записано в виде:
![]()
k
- волновой вектор,
![]() - частота колебаний, A(k)
– спектральные функции, т.е. это амплитуда
волны с определенным волновым числом.
- частота колебаний, A(k)
– спектральные функции, т.е. это амплитуда
волны с определенным волновым числом.
![]() ,
,
![]() .
.
В общем случае волновой вектор и частота связаны между собой. Эта связь осуществляется через дисперсионное уравнение:
![]() (6)
(6)
Это уравнение, как правило, вытекает из граничных условий задачи. В самом простом случае частота и характеристики среды не зависят от k, то есть, нет дисперсии среды.
Если рассматривать ЭМ волну в неограниченном пространстве, то уравнение (6) преобразуется к следующему соотношению:
![]() =
=![]() . (7)
. (7)
Т.к. параметры среды
![]() не зависят от k
– дисперсии нет.
не зависят от k
– дисперсии нет.
Амплитуда A(k)
определяется через значение величины
U(x,t)
в начальный момент времени:
![]() =
=![]() ,
тогда
,
тогда
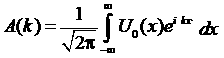 ,
,
![]() (8)
(8)
-
Монохроматическая волна.
Пусть начальное возмущение среды передается в виде гармонической волны.
![]() ,
где A=
,
где A=![]() .
.

![]()
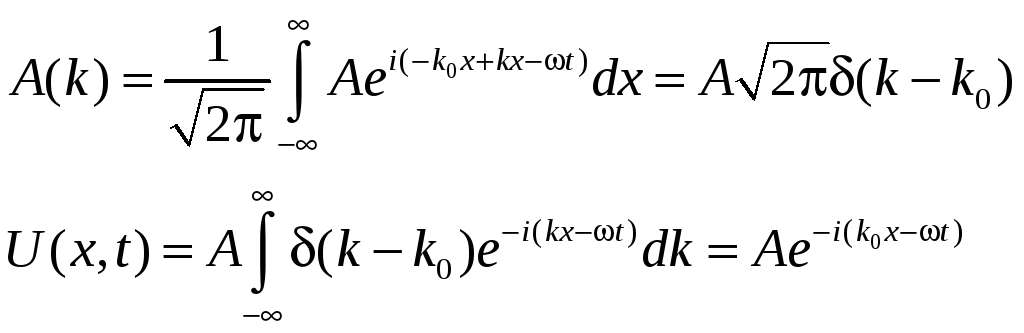
Где
![]() -
обобщенная функция, со свойствами:
-
обобщенная функция, со свойствами:
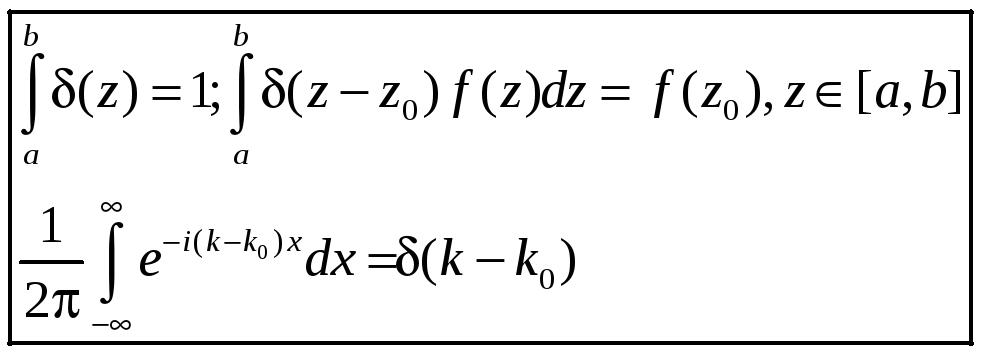
Тогда
![]()
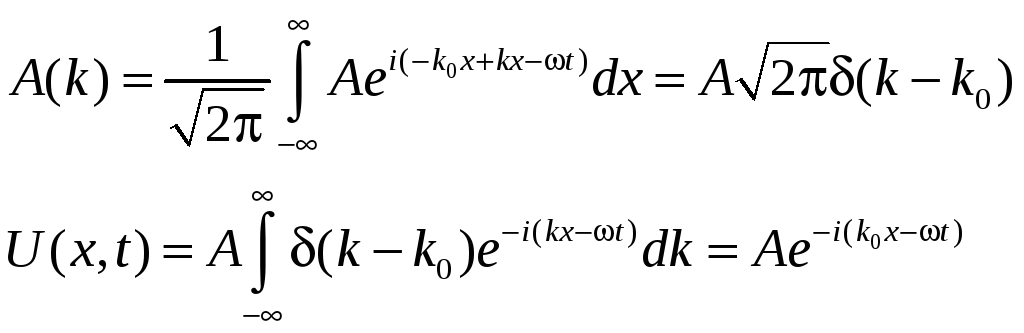 - монохроматическая
волна
- монохроматическая
волна
В многомерном случае:![]()
-
Характеристики линейных волн.
Реальная волна имеет следующие характеристики:
-
Амплитуда А, для линейной волны это const
-
Фаза волны
 ,
,
где k – волновой вектор
![]() - частота волны
- частота волны
Фаза не имеет
глубокого смысла. Имеет смысл разность
фаз:
![]()
для одномерной волны
![]() ,
где
,
где
![]() - начальная фаза
- начальная фаза
Для линейных волн фаза является линейной функцией времени и координат.
Волна в общем случае
будет записываться в следующем виде:
![]() .
.
Физический смысл имеет
реальная часть:
![]() .
.
В общем случае
![]() - это вектор.
- это вектор.
Если
![]() ,
то это поперечная волна (например,
электромагнитная волна
,
то это поперечная волна (например,
электромагнитная волна
![]() ).
).
Если
![]() ,
то это продольная волна (волны
пространственного заряда, распространенные
волны в веществе).
,
то это продольная волна (волны
пространственного заряда, распространенные
волны в веществе).
Волны, у которых
![]() могут быть плоскими (на плоскости),
цилиндрическими (в цилиндрическом
пространстве), сферическими(в сферическом).
могут быть плоскими (на плоскости),
цилиндрическими (в цилиндрическом
пространстве), сферическими(в сферическом).
