9. Непроцедурный язык Норма. Понятие сетки. Понятие области.

Н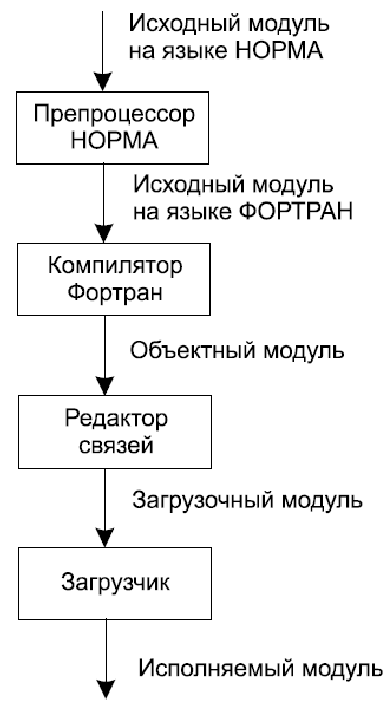ОРМА - предназначен для решения систем дифференциальных уравнений в частных производных методом сеток. Норма – отечественная разработка (в конце 70-х, начале 80-х). Норма – непроцедурный язык  отсутствие в программе явно описанной процедуры вычислений. Вместо этого – соотношения между вх. и вых. величинами и области применения этих соотношений. Транслятор понимается как препроцессор. Транслятор формирует процедуры для вычислений  он должен по написанным соотношениям определить не только прядок вычислений, но и возможность пар. счета.

Программа на языке НОРМА, состоящая из последовательности описаний, сначала обрабатывается препроцессором, формирующим на выходе прог-у на одном из языков прог-ания (Си, Фортран, Ассемблер), которые обрабатывае стандартными трансляторами. Основные понятия: ОБЛАСТЬ и оператор ПОЛАГАТЬ.

ДЛЯ <область> ПОЛАГАТЬ <список соотношений>

Оператор присваивания “:” служит для транслятора основой для определения порядка счета и не требует немедленного выполнения. | и {} – необязательный эл-нт.

<описание>::<описание скалярной величины>|<описание величины, определенной на сетке>|<описание индексной конструкции>|<описание параметров сетки>|<описание входных величин>|<описание выходных величин>

Простое выражение может включать в себя только специальные величины: параметры. Все параметры должны получить своё значение.

Пространственно-временная сетка представляет совокупность целочисленных наборов, каждый из которых представляет отдельный узел сетки. Сетку можно описать, именовать и производить над ней некоторые простые операции. Сетка представляет собой векторное N-мерное пространство, в котором определены N направлений, и с каждым таким направлением связано уникальное имя (индекс направления). Любая область является некоторой ограниченной частью такой сетки.

Условные области. 2 типа условных областей: условные подобласти и предикатные подобласти. Для получения первых используются две функции, имеющие один аргумент: ЛЕВ() и ПРАВ().

Пример: SN1:S/SI ЛЕВ(2)+ПРАВ(1) необходимо вернуться к одномерным областям.

→формируется условная подоблость SN1, получаемая из области S путем исключения из составляющей области SI слева двух точек и добавления справа одной точки.

Предикатная подобласть получается из исходной области включением в нее точек, для которых лог. выражение над заданными в узлах сетки переменными истинно.

Пример: Если S: (S1: (I=2…N) ; S2: (Y=1…M))

SA, SB : S/X + Y[I,J] – Z[J+1] > 0 (для SA – истина, SB – ложно)

В этом примере описываются две предикатные подобласти SA и SB. Переменные X, Y и Z должны быть заданы в узлах сетки. К подобласти SA относятся те узлы области S, для которых выполняется указанное неравенство. К подобласти SB относятся все остальные узлы. Очевидно, что SA  SB = 0 и SA  SB = S

10. Оператор полагать в языке норма.

В НОРМА основными понятиями являются ОБЛАСТЬ и оператор ПОЛАГАТЬ.

<ПОЛАГАТЬ>::=ДЛЯ <область> ПОЛАГАТЬ <список соотношений >

Этот оператор отличается от обычного оператора присваивания тем, что не требует немедленного присвоения значений переменным, указанным в списке соотношений.

При обработке оператора транслятор анализирует список соотношений для каждого узла области, определяет порядок вычислений и возможность параллельного счета.

Пример 1:

S: (1..M) – область «S»

S1: S / S-ЛЕВ(1) – подобласть «S1»

ДЛЯ S1 ПОЛАГАТЬ X[I]=X[I-1]+X[I+1]

В этом примере может быть реализован только последовательный счет.

Пример 2:

Пусть 1 ≤ i ,j ≤ 7

X_i,j = f_x (X_i-1,j+1, Y_i-1,j+2)

Y_i,j = f_y (X_i+1,j-1, Y_i+3,j-1)

Для второго примера можно составить две таблицы:

X

 i

1	1	1	1	1	1	1
1	2	2	2	2	2	2
1	7	6	4	4	4	3
1	8	8	7	6	5	5
1	10	9	9	8	7	6
1	12	11	10	10	9	8
1	4	13	12	11	11	10

Y

 i

6	5	3	3	3	1	1
7	7	5	5	4	1	1
9	8	7	6	6	1	1
11	10	9	8	7	1	1
13	12	11	10	9	1	1
14	13	13	12	11	1	1
1	1	1	1	1	1	1

В этих таблицах в каждой клетке записан номер шага, на котором можно вычислять значения соответствующих переменных. Сначала заполняются все клетки таблиц, соответствующие первому шагу вычислений, затем второму и т.д., пока не будут заполнены все таблицы. Из таблиц следует то, что возможно организовать параллельный счет, однако не наблюдается никакой регулярности перехода от одного шага к другому, что не дает возможности транслятору сгенерировать процедуру для регулярного счета. Транслятор с языка НОРМА изменяет содержание этих таблиц за счет увеличения общего числа шагов и организует параллельный регулярный счет.

X

 i

7	6	5	4	3	2	1
9	8	7	6	5	4	3
11	10	9	8	7	6	5
13	12	11	10	9	8	7
15	14	13	12	11	10	9
17	16	15	14	13	12	11
19	18	17	16	15	14	13

Y

 i

8	7	6	5	4	3	2
10	9	8	7	6	5	4
12	11	10	9	8	7	6
14	13	12	11	10	9	8
16	15	14	13	12	11	10
18	17	16	15	14	13	12
20	19	18	17	16	15	14

В этих таблицах показана возможность регулярного счета для элементов, лежащих на одной прямой (7-7-7). Наклон этих прямых одинаков для первой и второй таблицы, причем вычисление Х опережает вычисление для величины Y. Задача поиска уравнений прямых сходна с методом гиперплоскостей, однако здесь вычисление отдельных величин может «рассыпаться» по нескольким плоскостям. Т.о. метод гиперплоскостей → частный случай метода, реализованного на языке НОРМА.