Використання теореми Гауса-Остроградського для обчислення напруженості електричних полів.

1. Напруженість поля точкового заряду.

Знайти напруженість поля на відстані R від точкового заряду.

Fig 9

Обчислюємо потік вектора напруженості через сферу S.

2) Поле рівномірно зарядженої сфери радіусом R та зарядом Q.

_- поверхнева густина заряду рівна заряду на одиниці поверхні.

а), оточуємо сферу іншою сферою радіусом.

Fig 10

Ззовні сфери напруженість поля є аналогічна до напруженості поля, створеної точковим зарядом Q розміщеним в точці, що відповідає положенню центра сфери.

б). Шукаємо потік вектора E через малу сферу а це можливо лише тоді, коли . На цій основі побудований електростатичний захист, суть якого, що зовнішнє електричне поле в середину сфери не проникне.

Fig 11

2. Поле рівномірно зарядженої кулі.

Fig 12

а) Висновок як і в 2а

б)

Fig 13

4) Поле створене, рівномірно зарядженою площиною. Площина, з поверхневою густиною заряду σ.

Fig 14

Е-дотична до S бічн.;

оскільки, то

5) Поле створене напівбезмежним провідником.

Fig 15

Електричне поле в середину провідника не проникає, тому потік треба рахувати через верхнє дно циліндра і бокову поверхню.

6) Поле паралельно розміщених, різнойменно заряджених площин.

Fig 16 , (ззовні);

Висновок: Поле зосереджене всередині конденсатора, ззовні конденсатора поля нема.

Основна задача електростатики.

Електричне поле створюється зарядами, причому напруженість поля пропорційна Q (те саме стосується потенціалу). Заряди в просторі можуть бути розподілені:

1. дискретно ,…

2. з певною об’ємною густиною

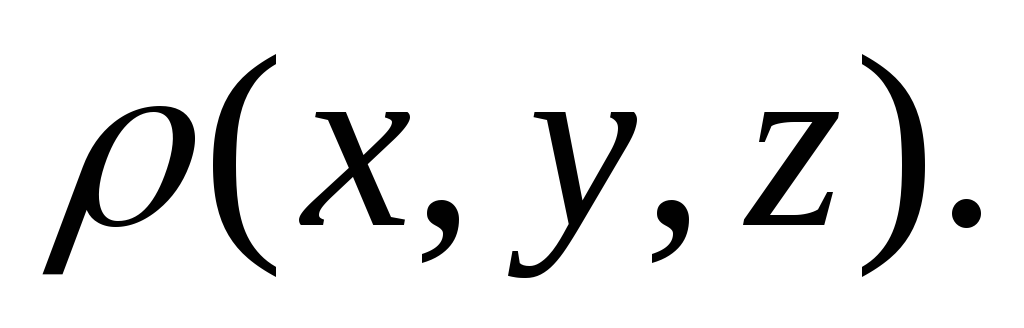
3. з певною поверхневою густиною

Який розподіл потенціалу і напруженості поля існує при даному просторовому розподілі заряду? (пряма задача).

Зворотна задача: Знайти той просторовий розподіл зарядів, який дає потрібний нам розподіл потенціалів і напруженостей?

Розв’язок даної задачі зводиться до розв’язку рівняння Пуассона.

- рівняння Пуассона.

Електричне поле в речовині.

Всі речовини умовно можна поділити на два класи: провідники і непровідники (діелектрики). Є ще напівпровідники.

В провідниках (це як правило метали) є вільні заряди які можуть вільно переміщуватись всередині провідника. Носієм негативного заряду є електрони -, а носієм позитивного заряду протони . Кл – елементарний заряд.

Всяка речовина, яка перебуває в нормальному стані звичайно є нейтральна, тобто кількість електронів і протонів однакова. Якщо в зразку є негативний заряд, то в ньому надлишок електронів, якщо речовина заряджена позитивно, то в ній недостача електронів.

Провідники мають таку хімічну будову, що валентні електрони атомів цих речовин зв’язані із своїми ядрами достатньо слабо, і тому практично вільно переміщаються в провіднику. В діелектрику всі валентні електрони приймають участь у створенні хімічних зв’язків, а тому локалізовані біля своїх атомів. Напівпровідники займають середнє положення між провідниками і діелектриками, тобто в цих речовинах мало вільних зарядів. В принципі, будь-яка речовина за певних умов може стати провідником.