Енергетична характеристика поля. Потенціал.

Введемо нову величину - потенціал, який рівний - потенціал даної точки поля. Фізичний зміст: потенціальна енергія одиничного позитивного заряду в даній точці поля. Для центрального симетричного поля, створеного точковим зарядом .

Введений таким чином потенціал знайдений з точністю до константи інтегрування, бо фактично ми отримали зміну потенціальної енергії, а не саму потенціальну енергію.

При логічно, що , тоді .

Отже ми прийшли до того, що - потенціал електричного поля, створений точковим зарядом в точці з радіусвектором . Потенціал є скалярною величиною.

Для гравітаційного поля: - потенціальна енергія одиничної маси в точці з координатою . Потенціал являє собою енергетичну характеристику силового поля .

Силова характеристика поля. Напруженість

1.,

2..

З цих виразів можна знайти силу, що діє на одиничний заряд (одиничну масу) в даній точці поля. Припустимо, що ; . Тоді:

1. при ;

2.; при

-напруженість є характеристикою даного поля і не залежить від величини пробного заряду (чи маси) та залежить від координати. Це є векторна величина. Для електричного поля має напрямок сили, що діє на одиничний пробний заряд, для гравітаційного поля має напрямок в якому менше тіло притягається до більшого.

, .

Зв'язок напруженості з потенціалом.

- напруженість поля в точці з координатою ;

- потенціал поля в точці з координатою .

Виконання роботи проти сил поля приводить до збільшення потенцільної енергії.

, ,, ;

.

Інтегральний вираз: (інтегруємо від початкового до кінцевого положення) ∆.

Принцип суперпозиції полів.

Якшо силове поле створене декількома джерелами, то напруженість сумарного поля в точці з координатою дорівнює векторній сумі напруженостей полів, створених в даній точці кожним джерелом: .

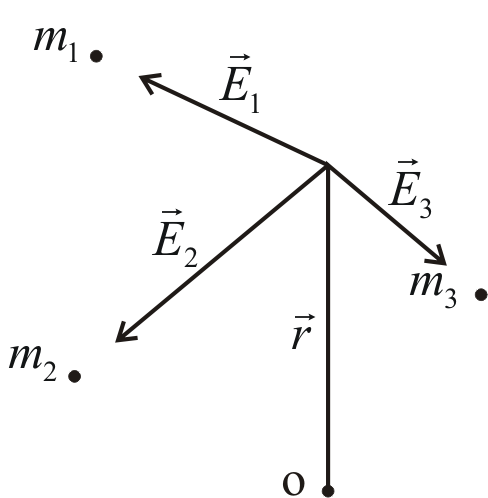
Fig 3

Для електричних полів це також справедливо (тут слід враховувати знаки).

Для суперпозиції потенціалів справедлива така сума: , яка є скалярною.

Fig 4

Кожний силовий центр діє на кожну частинку не залежно від інших.

Графічне зображення силових потенціальних полів.

1. Метод ліній векторів напруженості: якесь довільне поле зображене за допомогою кривих, які називають лініями силової напруженості.

Fig 5

Дотична до кривої вказує напрямок . Задати величину вектора можна за допомогою густоти розміщення ліній, тобто чим більша напруженість, тим більше силових ліній на одиницю площі.

Приклад:

а.Поле позитивного заряду б.Поле негативного заряду

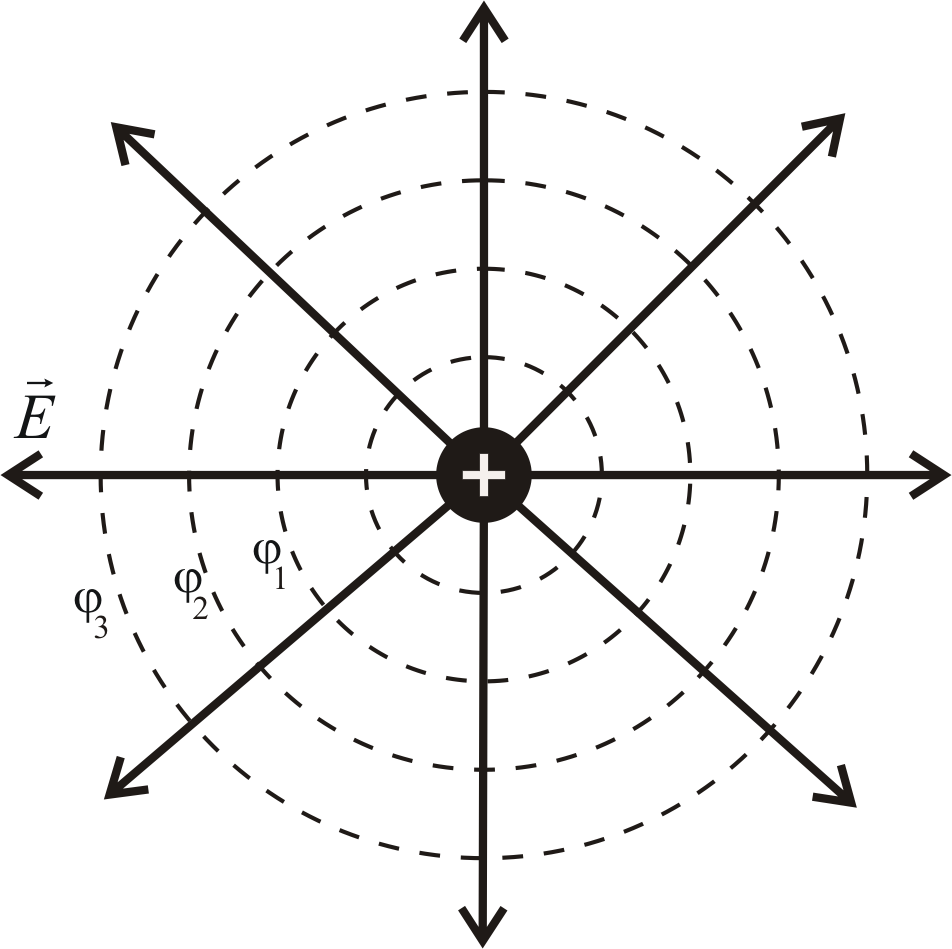
- напруженість поля створеного одиничним електричним зарядом.

в.Плоский конденсатор:

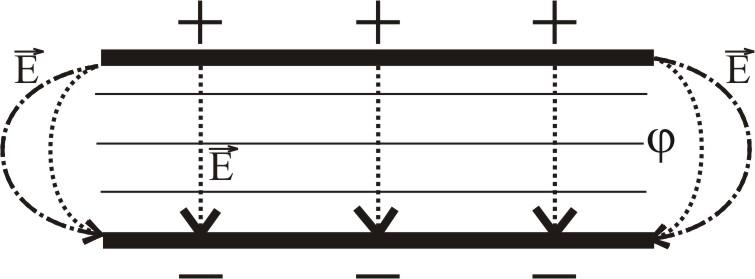
Fig 6

2. Метод еквіпотенціальних поверхонь (метод поверхонь рівного потенціалу): будується поверхня, для якої в кожній точці потенціал є сталим. Для поля точкового заряду еквіпотенціальні поверхні являють собою концентричні сфери з центром, який співпадає з положенням точкового заряду. , , і т.д.

Твердження: Силові лінії в точках перетину з еквіпотенціальними поверхнями перпендикулярні до них.

Якшо говорити про електростатичне поле, то сила взаємодії між зарядами залежить від середовища в якому перебуває заряд. Для вакууму закон Кулона запишеться у вигляді: , а для середовища: , де - відносна діелектрична проникність середовища, фізичний зміст якої є такий:

сила взаємодії в середовищі є в раз менша ніж сила взаємодії у вакуумі (, лише в вакуумі ).

Fig 7

Аналогічно для напруженості полів .

При переході з одного середовища в інше напруженість поля змінюється стрибком, це не завжди зручно, тому було введено вектор (вектор електричного зміщення, або електричної індукції), який зберігається при переході з одного середовища в інше. і т. д.

Вводимо вектор і він справедливий на всі випадки життя.

Уточнення: Нормальна складова вектора зберігається.

Теорема Гауса-Остроградського.

Потік вектора електричного зміщення через довільну замкнену поверхню дорівнює сумарному заряду, який знаходиться в об’ємі, обмеженому цією поверхнею.

_- теорема Гауса – Остроградського.

Fig.8

E_ldl – циркуляція вектора вздовж кривої;

E_ndS – потік вектора через поверхню;

, де - об’ємна густина заряду дорівнює заряду, який припадає на одиницю об’єму. Де Q – неперервний заряд в просторі; а τ – одиничний об’єм; – дискретний заряд;

Тобто – перше рівняння Максвелла для електромагнітного поля.