Cкладання коливань

1)Складання коливань одного напрямку;

а) складання коливань однакової частоти.

................................

Для складання коливань одного напрямку і одної частоти використовують метод вектора амплітуди: будують вектор по величині рівний амплітуді з кутом рівним початковій фазі.

При t=0,

Fig 93

Якщо розпочати обертати вектор А з кутовою швидкістю

проти годинникової стрілки, то в певний момент часу проекція А на вісь х дає миттєве значення х. Період коливань рівний часу одного обертання.

За даним методом складання коливань зводиться до складання відповідних векторів амплітуди.

Fig 94

Кінцеве

б)складання коливань з близькими частотами

сумарне коливання називається биттям і виглядає так:

Fig 95

2) Складання взаємноперпендикулярних коливань. Фігури Лісажу

Треба знайти суму коливань однієї частоти, взаємноперпендикулярних напрямів

α = 0

α = π

α =

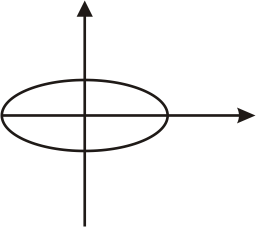
Отже, в загальному випадку в нас є еліпс:

При a = b рух по еліпсу вироджується в рух по колу. Якщо частоти неоднакові, то рух дуже складний, якщо частоти кратні, то вийдуть фігури, які можна наперед вгадати, вони називаються фігурами Ліссажу.

:

Fig 96

Згасаючі коливання (коливання при наявності втрат)

- рівняння згасаючих коливань.

протилежна до швидкості: вважатимемо, що пропорційна до v. Це припущення є правомірне при не дуже великих швидкостях.

Тоді рівняння руху запишеться як: . Позначимо і . Тоді перепишемо рівняння руху . Для коливного контура

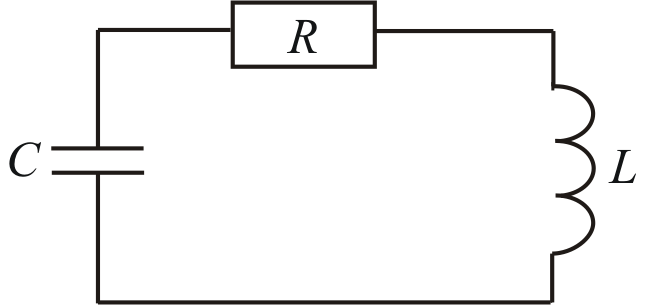
Fig 97

виходимо з другого правила Кірхгофа: . Позначимо . Розв’язок цього рівняння шукаємо в такому вигляді:

Підставляємо дані рівності і отримаємо:

, при t = 0 , - початкова амплітуда. Підставимо в перше рівняння : . При наявності опору частота коливань зменшується. Зокрема, якщо опір дуже великий коливання взагалі зникають, і є аперіодичне (неперервне) наближення системи до положення рівноваги.

Fig 98

Як бачимо з графіку, огинаюча є експонентою.

Характеристики згасаючих коливань

1). Коефіцієнт згасання – (характеризує опір середовища).

Фізичний сенс – величина обернена до часу протягом якого амплітуда коливань зменшеться в разів (). τ – час, протягом якого амплітуда коливань зменшується в е разів.

2). Декремент згасання рівний відношенню двох послідовних амплітуд, тобто

3). Логарифмічний декремент згасання:

. Фізичний зміст логарифмічного декременту згасання полягає в тому, що він є величиною оберненою до числа повних коливань протягом яких амплітуда зменшується в разів.

4). Добротність коливної системи: π/Δ

Вимушені коливання

- вимушуюча сила. Тоді рівняння руху запишемо як :

(механічні коливання)

(електричні коливання)

Отримали два неоднорідні рівняння:

Розв'язки однорідних рівнянь запишуться як:

Дані два розв’язки є розв’язками однорідного рівняння. Із зменшенням часів коливань їх внесок в сумарне коливання буде пропадати, і при достатньо великих періодах коливань власні (вільні) коливання будуть згасати і залишаться лише вимушені коливання. В початковий момент часу амплітуда вимушених коливань рівна нулеві, потім протягом певного часу ця амплітуда буде зростати, тобто буде проходити встановлення вимушених коливань. Іншими словами, в той момент часу, коли власні коливання згаснуть вимушені коливання можуть набрати свого стаціонарного стану.

Fig 99

Знайдемо частковий розв’язок неоднорідного рівняння (для достатньо великого часу):

- амплітуда незалежна від часу.

Підставляємо в рівняння згасаючих коливань :

^.

Перетворимо знаменник до вигляду :

З цієї рівності випливає, що амплітуда коливань .

Для вимушених коливань в електричному контурі:

.

Вимушене коливання відстає по фазі від вимушуючої сили на кут , і цей кут тим більший чим більший опір середовища. Коли то зсув фаз рівний . Величина амплітуди коливань залежить від знаменника :

коли

<,

- частота власних коливань при наявності опору.

Тоді резонансна амплітуда коливань: . При резонансі

.

Fig 100

, . Бачимо, що при і , амплітуда прямує до нескінченності ().