Використання пучків заряджених частинок

1. Електронно-променеві прилади(кінескоп, осцилографічні трубки,індикаторські трубки для військових,електронні вакуумні комутатори);

2. Електронні мікроскопи і електрографи – прилади, які дозволяють вивчати будову речовини з допомогою електронних пучків.

3. Масспектрометрія – можна перетворити атоми і молекули речовини в іони, а потім ці іони розділити між собою в залежності від питомого заряду. Масспектрометрія дозволяє здійснювати дуже точний хімічний аналіз.

4. Прискорювачі заряджених частинок.

Взаємні перетворення електричних і магнітних полів

1. Явище електромагнітної індукції.

Якщо відбувається зміна магнітного потоку, що пронизує якийсь замкнутий контур, то в цьому контурі виникає електричний струм. Цей струм називається індукційним, а (електрорушійна сила індукції пропорційна швидкості зміни магнітног потоку).

В системі СІ (мінус за законом Ленца: напрямок індукційного струму такий, що його магнітне поле протидіє причині, яка викликала появу струму).

Якби не було явища електромагнітної індукції то не було б генераторів електричного струму (не було б трансформаторів).

Індукційний струм деколи виникає в масивних предметах, цей струм називають струмом Фуко, тобто якщо масивний предмет пронизує змінний струм, то в цьому предметі виникає струм Фуко, бо опір предмета є малий.

Струмами Фуко можна нагрівати предмети, є спеціальні печі, де струмами Фуко плавлять тугоплавкі речовини.

Явище самоіндукції

Суть явища полягає у виникненні електрорушійної сили індукції при зміні власного магнітного поля контуру. Якщо, по контуру протікає електричний струм І, то при цьому контурну площадку пронизує певний магнітний потік. Величина магнітного поля тим більша, чим більший електричний стум()

Fig 70

Ми отримали, що , , де L - певний коефіцієнт пропорційності, який залежить від геометрії контура і від магнітних властивостей середовища.

L=Ф, якщо І=1, тобто L- індуктивність контура чисельно рівна магнітному потокові, який пронизує контур при протіканні по контуру струму величиною в 1А.

Якщо вважати В сталим, то зміна Ф може проходити лише за рахунок струму І, а тому ; то .

Звідси L чисельно рівний , якщо (швидкість зміни струму)

Індуктивність соленоїда:

Fig.71

; - довжина котушки;

Ф₁(один виток пронизує потік)=BS, де S- площа, яку обмежує один виток.

;; , тут - об’єм (дана рівність справедлива для тороїда але не досить точна, бо для тороїда поле неоднорідне).

Наростання і спад струму в колі з індуктивністю.

Енергія магнітного поля

Спадання струму в колі з індуктивністю:

Fig 72

Якщо включити ключ в положення 1,то в колі протікатиме струм І₀: .

Якщо ключ перевести в положення 2 (розірвати коло), записавши 2-ге правило Кірхгофа отримаємо:.

Використавши початкові умови, одержимо

t=0, I=I₀ (в момент вимкнення); t=0, lnI=lnI₀ C₀=I₀ значить . Або ; де - постійна часу ; і якщо ,то ми отримаємо в раз менший струм.

Fig 73

Наростання струму в колі з індуктивнівстю:

Вмикаємо коло, і при t=0, I=0. Використовуючи друге правило Кірхгофа запишемо наступне рівняння : . Тоді , де - частковий розв’язок неоднорідного рівняння. Вводиться з наступних умов : при , а ; при , . Тоді .

Fig 74

Енергія магнітного поля:

При наростанні струму в контурі повинна виконуватись якась робота проти , в результаті цього струм набуває свого максимального значення поступово, і навпаки, після вимикання струму, струм в колі теж зникає поступово. Протікання цього струму підтримується за рахунок дії . Тобто в контурі з певною індуктивністю , при протіканні через нього струму , існує певний запас енергії, який набувається під час наростання струму і втрачається при вимиканні кола. Величину цієї енергії знайдемо як роботу проти в процесі наростання струму. (знак мінус, оскільки робота виконується проти ), 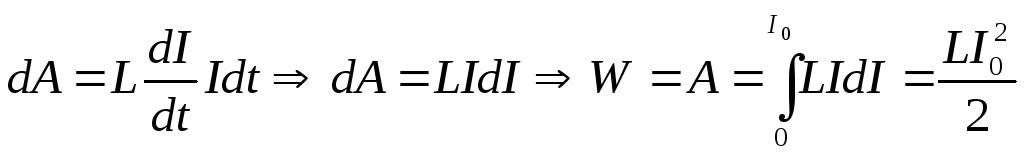. Якщо говорити більш загально, то . Запишемо вираз для індуктивності соленоїда : . Підставивши його у попереднє рівняння отримаємо енергію магнітного поля соленоїда : , де - енергія, що припадає на одиницю об’єму. Якщо розглядати просторову залежність густини енергії, то .В загальному випадку густина енергії магнітного поля , а густина енергії електричного поля . Як бачимо вирази дуже подібні між собою.