Рух заряджених частинок в електричних та магнітних полях. Рівняння руху та енергія зарядженої частинки в електромагнітному полі

- сила, що діє на заряджену частинку в електричному полі. В магнітному полі діє сила . Тоді в електромагнітному полі на заряджену частинку діятиме сила . З другого закону Ньютона . Підставимо даний вираз у верхнє рівняння і отримаємо: - рівняння руху зарядженої частинки в електромагнітному полі. В залежності від координати це рівняння поділяється на 3.,,, де - питомий заряд частинки. Ці рівняння відповідають системі рівнянь.Тепер помножимо рівняння руху скалярно на :, очевидно, що . Тоді наше рівняння можна записати як , або . Оскільки . В кінцевому результаті ми отримаємо:.

Вся зміна кінетичної енергії в електромагнітному полі (заряджена частинка) проходить за рахунок потенціальної дії на частинку. Магнітна складова не змінює енергії частинки. Сумарна енергія частинки залишається сталою.

Приклади розв’язання рівняння руху заряджених частинок.

1. Рух зарядженої частинки в однорідному електричному полі:

Fig 66

Відомо, що в електричному полі на заряджену частинку діє сила . Введемо початкові умови : ; ; - наявна лише складова поля. Запишемо рівняння руху зарядженої частинки :

З початкових умов тоді рівняння руху описуватиме параболу, що лежить в площині z = 0.

2. Рух зарядженої частинки в однорідному магнітному полі:

Fig 67

- наявна лише складова поля.Нехай (лежить в площині XOZ)=;

Тепер запишемо рівняння руху зарядженої частинки для даного випадку: ; ; , - довільне; і коли .

По осі Z рух рівномірний. Для осей X та Y : .

Припускаємо що ; t=0; (бо інакше система рівнянь не виконується). Тоді :, а . Розв’язком даних рівнянь є довільна гармонічна функція:, де - циклотронна частота, а . В кінцевому вигляді рівняння руху запишемо так:

- маємо рух по колу радіуса A, причому центр кола зсунений по осі X від початку координат на величину . Тіло рухається по гвинтовій лінії вісь якої паралельна до осі Z, обертання по колу здійснюється з кутовою швидкістю ; тобто – період обертання, причому крок гвинта:

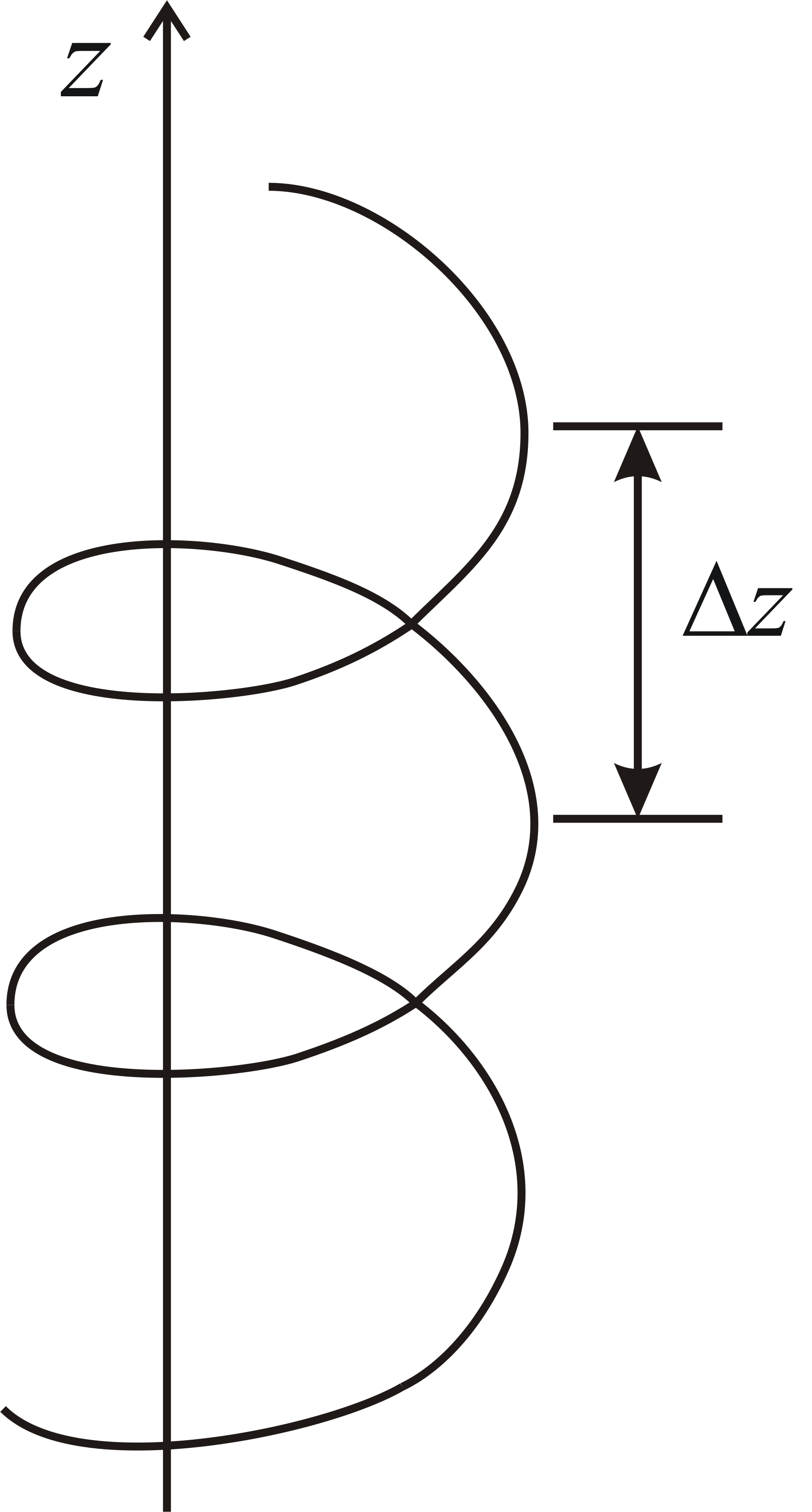
Fig 68

Коли , то магнітне поле не буде впливати на рух частинки. Якщо початкова швидкість не мала Z складової, то тіло рухається по колу в площині паралельній до XOY. Оцінимо швидкість руху частинки по колу:

. Отже А-радіус кола, по якому рухається частинка.

3. Ефект Холла(Hall)

Fig 69

Ефект Холла полягає у виникненні поперечного електричного поля в зразку, в якому протікає струм, і цей зразок поміщений в магнітне поле перпендикулярно до струму.

-напруга Холла;

Прикладене магнітне поле закручує траєкторію носіїв струму. В результаті, біля однієї стінки зразка є надлишок носіїв струму, а біля іншої їх недостача, тобто виникає поперечне електричне поле. Нагромадження носіїв струму біля однієї стінки триває доти, поки сила Лоренца, яка закручує траєкторії носіїв струму не зрівноважиться з силою, яка діє з боку поля Холла: ;

;

;

- постійна Холла;

, де - ширина зразка. може бути як позитивне так і негативне. Якщо носії струму електрони, то , n - концентрація носіїв струму. Якщо носії струму позитивні, то . Дослідження ефекту Холла дозволяє прямим чином визначити знак і концентрацію носіїв струму.