
- •Введение
- •1.Расчёт детали на усталостную прочность
- •1.1. Техническое задание
- •1.2. Расчёт коэффициента запаса прочности
- •2. Расчет напряженного резьбового соединения
- •2.1 Проектировочный расчет болта
- •2.2 Проверочный расчёт болтового соединения на прочность.
- •3. Расчёт узла привода
- •3.1. Энерго-кинематический расчёт узла привода
- •3.2 Расчет косозубой цилиндрической передачи
- •3.2.1 Проектировочный расчет передачи по контактной выносливости зуба
- •3.2.2. Проверочный расчет зубьев на контактную выносливость
- •3.2.3 Проверочный расчет зубьев на изгибную выносливость
- •3.2.4 Проверочный расчет зубчатой передачи при перегрузке
- •3.3 Расчёт размеров шестерни прямозубой цилиндрической передачи.
- •3.4 Расчёт и проектирование промежуточного вала на опорах качения.
- •3.4.1 Проектировочный расчёт вала.
- •3.4.2. Выбор и проверочный расчет подшипников качения
- •3.4.3. Выбор и проверочный расчёт шпонок
- •3.4.4. Проверочный расчет промежуточного вала
- •Список литературы
Санкт-Петербургский Государственный Политехнический университет
Кафедра машиноведения и деталей машин
ОСНОВЫ РАСЧЁТОВ НА ПРОЧНОСТЬ
Пояснительная записка
Курсовая работа
Студент группы 2033/2______________________________(А.А. Генералов)
Руководитель _______________________________(А.А. Ашейчик)
Санкт-Петербург
2011
Оглавление
Введение
1. Расчет детали на усталостную прочность
-
Техническое задание
-
Расчет коэффициента запаса прочности
2. Расчет напряженного резьбового соединения
2.1 Проектировочный расчет болта
-
Проверочный расчет болта на прочность
3. Проектирование узла привода
-
Энергокинематический расчет узла привода
-
Расчет косозубой цилиндрической передачи
-
Проектировочный расчет передачи по контактной выносливости зуба
-
Проверочный расчет зубьев на контактную выносливость
-
Проверочный расчет зубьев на изгибную выносливость
-
Проверочный расчет зубьев при перегрузках
-
Расчет размеров шестерни прямозубой цилиндрической передачи
-
Расчет и проектирование промежуточного вала на опорах качения
-
Проектировочный расчет вала
-
Выбор и проверочный расчет подшипников качения
-
Выбор и проверочный расчет шпонок
-
Проверочный расчет промежуточного вала
Список литературы
Приложение

Введение
Целью данной работы являлся расчет некоторых типовых деталей и узлов по критерию прочности.
Данная работа может быть разделена на три части.
В первой части проводится проверочный расчет штока паровой машины по критерию усталостной прочности.
Во второй части проводится проектировочный расчет напряженного резьбового соединения по критерию статистической прочности, а также проверочный расчёт болтового соединения по критерию усталостной прочности и герметичности.
Заключительная часть работы посвящена проектированию узла привода. В данном разделе осуществляется энергокинематический расчет узла привода, проектировочный расчет косозубой цилиндрической передачи по критерию контактной выносливости, проверочный расчет зубьев по критерию контактной и изгибной выносливости, проводится проектировочный расчет вала по критерию статической прочности вала на кручение, выполнен проверочный расчет подшипников качения по критерию динамической грузоподъемности, а также проектировочный расчет шпонок по критерию статическая прочность на смятие.
1.Расчёт детали на усталостную прочность
1.1. Техническое задание
Шток гидроцилиндра перемещает ползун в прямом и обратном направлениях с усилиями F1 и F2 соответственно.
Определить
запас прочности шейки штока, если
требуемый ресурс составляет 2 105
двойных ходов.
105
двойных ходов.
Схема
механизма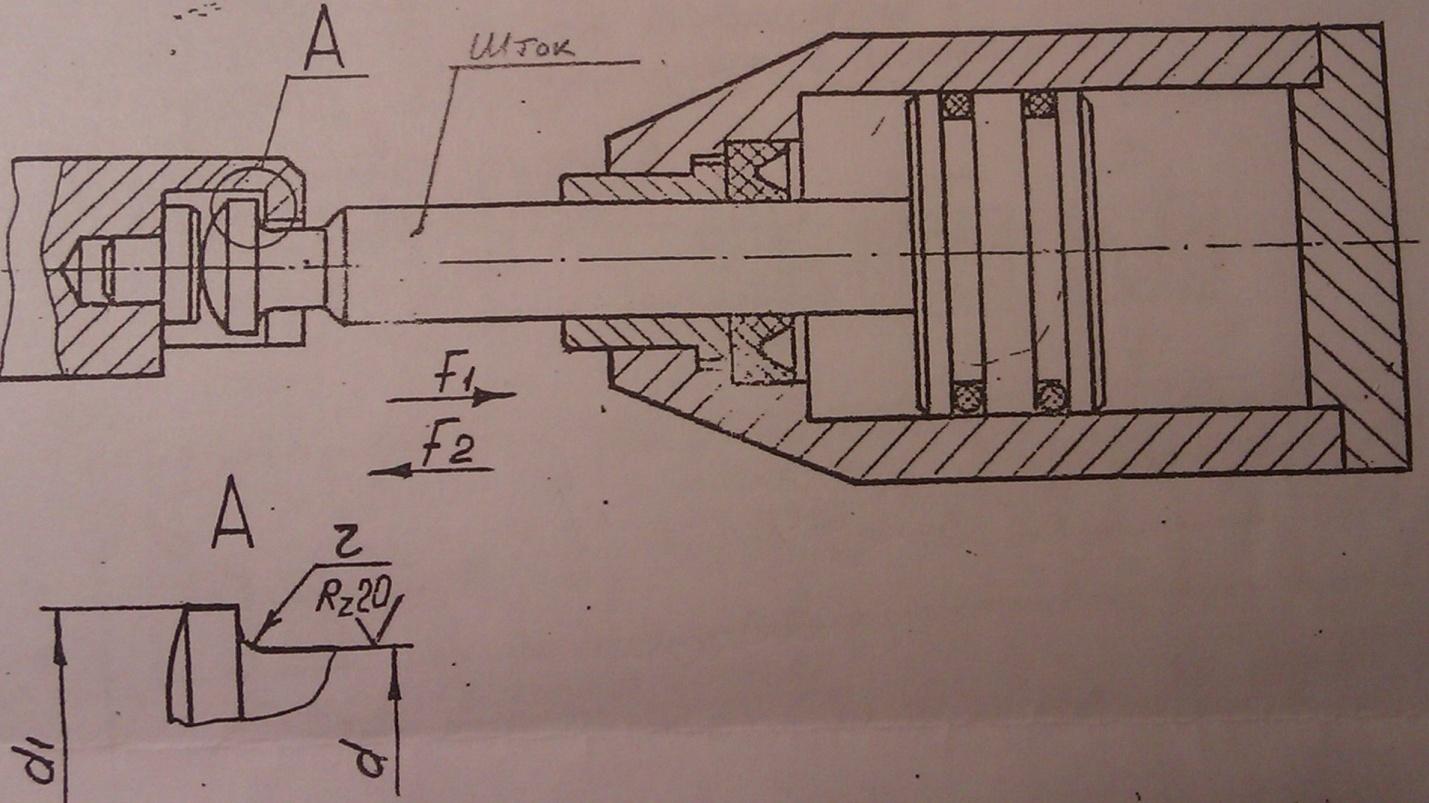
Рис. 1.1
Таблица 1.1
Исходные данные
|
№ варианта |
d, мм |
d1, мм |
r, мм |
F1, кН |
F2, кН |
Материал штока |
|
3 |
25 |
32 |
2,5 |
45 |
40 |
Сталь 40Х |
1.2. Расчёт коэффициента запаса прочности
В данном разделе необходимо определить фактический коэффициент запаса прочности штока гидроцилиндра, а также проверить условие прочности.
Вероятный вид разрушения – усталостная поломка.
Критерий расчёта – усталостная прочность.
Коэффициент запаса прочности может быть определён по формуле
S= ,
(1.1)
,
(1.1)
\где
S
– фактический коэффициент запаса; σпр
– предельное напряжение,
 ;
σmax
– максимальное фактическое напряжение,
;
σmax
– максимальное фактическое напряжение,
 .
.
Максимальное фактическое напряжение σmax определим по формуле
σmax= ,
(1.2)
,
(1.2)
где F1 – усилие штока при растяжении (рис 1.1), Н; Amin – минимальная площадь, мм2.
Минимальную площадь опасного сечения штока найдём по формуле
Amin= , (1.3)
, (1.3)
где d – диаметр опасного сечения, мм.
Подставив числа в формулу (1.3), найдём минимальную площадь опасного сечения штока
Amin= =
490 мм2
=
490 мм2
Подставляя численное значение Amin в выражение (1.2), получаем
 =
= = 91,8
= 91,8

Найдём σmin по формуле
σmin= ,
(1.4)
,
(1.4)
где F2 – усилие штока при сжатии, Н.
Подставляем численные значения в выражение (1.4)
 =
=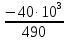 = -81,6
= -81,6

Построим график изменения напряжения в штоке (рис. 1.2)
Цикл изменения напряжения

Рис. 1.2
Из
рассмотрения рис. 1.2 следует, что в
качестве предельных напряжений σпрследует
выбрать предел усталости при произвольном
цикле для детали при ограниченном числе
циклов
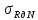 ,
так как опыт эксплуатации подобных
механизмов показывает, что причиной их
,
так как опыт эксплуатации подобных
механизмов показывает, что причиной их
разрушения
является усталостная поломка.
 определяется по формуле [1, с.33].
определяется по формуле [1, с.33].
 =
=
 <
< , (1.5)
, (1.5)
где
 – предел усталости при произвольном
цикле для детали и ограниченном числе
циклов,
– предел усталости при произвольном
цикле для детали и ограниченном числе
циклов,
 ;
;
 – предел усталости при симметричном
цикле и ограниченном числе циклов для
детали,
– предел усталости при симметричном
цикле и ограниченном числе циклов для
детали,
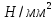 ;
R
– коэффициент асимметрии цикла;
;
R
– коэффициент асимметрии цикла;
 – коэффициент чувствительности детали
к асимметрии цикла.
– коэффициент чувствительности детали
к асимметрии цикла.
Определим коэффициент ассиметрии цикла
R
=
 (1.6)
(1.6)
R
=
 = -0,890
= -0,890
Определим
предел усталости при симметричном цикле
и ограниченном числе циклов
 по формуле [1, с.30]
по формуле [1, с.30]
 =
=
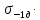 К0
(1.7)
К0
(1.7)
где
К0
– коэффициент, учитывающий количество
циклов;
 – предел длительной выносливости для
детали при симметричном цикле,
– предел длительной выносливости для
детали при симметричном цикле,
 ,
который определяется по формуле [1, с.20]
,
который определяется по формуле [1, с.20]
 =
=
 (1.8)
Учитывая материал штока – Сталь 40Х
и зная, что
(1.8)
Учитывая материал штока – Сталь 40Х
и зная, что
 = 670
= 670
 ,
,
 =500
=500 [1, с.74], найдём предел выносливости
гладкого стандартного образца
[1, с.74], найдём предел выносливости
гладкого стандартного образца
 по формуле [1, с.77]
по формуле [1, с.77]
 =
0,4
=
0,4
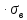 = 270
= 270
 (1.9)
(1.9)
Определим значение коэффициента снижения предела выносливости К, который учитывает влияние различных факторов, по формуле [1, с.21]
К
=
 ,
(1.10)
,
(1.10)
где – коэффициент концентрации напряжений;
– коэффициент концентрации напряжений;
 – коэффициент, учитывающий масштабный
фактор;
– коэффициент, учитывающий масштабный
фактор;
 – коэффициент, учитывающий шероховатость
поверхности штока;
– коэффициент, учитывающий шероховатость
поверхности штока;
 – коэффициент, учитывающий упрочняющие
технологии;
– коэффициент, учитывающий упрочняющие
технологии;
 – коэффициент, учитывающий анизотропию
материалов.
– коэффициент, учитывающий анизотропию
материалов.
Так
как в данном случае деталью является
шток, следовательно, заготовка представляет
собой прокат вдоль волокон, то есть
 =1
[1, с.29]. Считая, что дополнительная
обработка не производилась, принимаем
=1
[1, с.29]. Считая, что дополнительная
обработка не производилась, принимаем
 = 1.
= 1.
Определим по формуле [1,с.22]
по формуле [1,с.22]
 =
1+q(
=
1+q( ,
(1.11)
,
(1.11)
где
q
– коэффициент чувствительности металла
к концентрации напряжений;
 – теоретический коэффициент концентрации
напряжений.
– теоретический коэффициент концентрации
напряжений.
Найдём
 по графику [1, с.78]. Учитывая, что
по графику [1, с.78]. Учитывая, что
 =
=
 = 1,28 и
= 1,28 и
 =
=
 = 0,1, получаем
= 0,1, получаем
 = 1,68.
= 1,68.
При
 =
=
 = 0,74 коэффициент чувствительности
металла к концентрации напряжений q=0,9
[1, с.84]
= 0,74 коэффициент чувствительности
металла к концентрации напряжений q=0,9
[1, с.84]
Подставляя полученные значения в выражение (1.11), получаем
 =
1+0,9
=
1+0,9
 (1,68 - 1) = 1,61
(1,68 - 1) = 1,61
Коэффициент
 при d
=25 мм будет равен
при d
=25 мм будет равен
 =
0,92 [1, с.85], а коэффициент
=
0,92 [1, с.85], а коэффициент
 при
при
 =670
=670 и R
= 20 мкм будет равен
и R
= 20 мкм будет равен
 =
0,71 [1, с.85].
=
0,71 [1, с.85].
Подставим численные значения в формулу (1.10) и вычислим К
К
=
 =
2,15
=
2,15
Подставляем
численные значения в формулу (1.8) и
вычисляем

 =
=
 =
125
=
125

Определим К0 по формуле [1, с.30]
К0= ,
(1.12)
,
(1.12)
где
 – базовое число циклов напряжений,
соответствующее точке перелома кривой
усталости; N
– число циклов; m
– показатель степени кривой усталости.
– базовое число циклов напряжений,
соответствующее точке перелома кривой
усталости; N
– число циклов; m
– показатель степени кривой усталости.
 принимаем
равным
принимаем
равным
 =
2
=
2 106
циклов [1, с.30].
106
циклов [1, с.30].
Считая,
что С=5+ ,
определяем m
по формуле [1, с.30]
,
определяем m
по формуле [1, с.30]
m= =
= =
6,0 (1.13)
=
6,0 (1.13)
Подставляем значения в выражение (1.12)
К0= = 1,46
= 1,46
Подставляем значения в выражение (1.7), получаем
 =
125
=
125 1,46
= 183
1,46
= 183
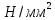
Определим коэффициент чувствительности детали к асимметрии цикла по формуле [1, с.31]
 =
= ,
(1.14)
,
(1.14)
где
 – коэффициент чувствительности к
асимметрии цикла, который может быть
найден по эмпирической формуле [1, с.31]
– коэффициент чувствительности к
асимметрии цикла, который может быть
найден по эмпирической формуле [1, с.31]
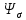 =
0,02+2
=
0,02+2 10-4
10-4 =
0,02+2
=
0,02+2 10-4
10-4 670=
0,154 (1.15)
670=
0,154 (1.15)
Подставляем численные значения в выражение (1.14)
 =
= =
0,071
=
0,071
Теперь
может быть вычислен предел усталости
в произвольном цикле для детали при
ограниченном числе циклов
 .
.
Подставляем численные значения в выражение (1.5)
 =
=
 =
192
=
192

Так
как
 =192
=192
 =500
=500 ,
то
,
то
 =
= =
192
=
192
 .
.
Проверим условие прочности для данного штока
S [S]
(1.16)
[S]
(1.16)
Вычисляем
фактический коэффициент запаса прочности
S
по формуле (1.1), принимая
 =
= ,получаем
,получаем
S= =
2,1
=
2,1
В данном случае, принимая во внимание то, что исходные данные и результаты расчёта имеют пониженную точность, назначаем нормативный коэффициент запаса прочности [S] равным 2,00 [1, с.87].
Таким
образом видно, что S=2,1
 [S]=2,00.
То есть при изготовлении штока из стали
40Х по указанным в техническом задании
размерам, будет обеспечено отсутствие
усталостной поломки при заданных
нагрузках и ресурсе в 2
[S]=2,00.
То есть при изготовлении штока из стали
40Х по указанным в техническом задании
размерам, будет обеспечено отсутствие
усталостной поломки при заданных
нагрузках и ресурсе в 2 105
двойных ходов, без дополнительной
обработки поверхности штока в опасном
сечении.
105
двойных ходов, без дополнительной
обработки поверхности штока в опасном
сечении.
