
6.2.3. Повне внутрішнє відбиття
Явище повного внутрішнього відбиття
від поверхні розділу середовищ може
відбуватися тоді, коли кут падіння
більший від граничного.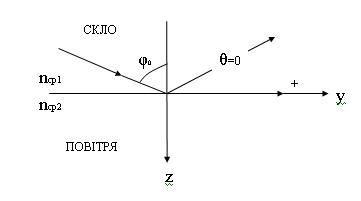 Тобто, це можливо при умові:
Тобто, це можливо при умові:
![]() .
Тоді, згідно закону Снелліуса
.
Тоді, згідно закону Снелліуса
![]() при
при
![]() :
:
![]()
![]()
![]() – кут повного внутрішнього відбивання.
В першому середовищі швидкість
поширення вздовж осі Y:
– кут повного внутрішнього відбивання.
В першому середовищі швидкість
поширення вздовж осі Y:
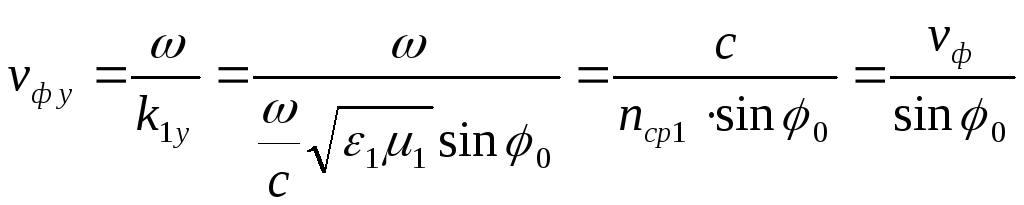 ,
тобто швидкість поширення вздовж осі
Y має
,
тобто швидкість поширення вздовж осі
Y має
![]() (оскільки значення
(оскільки значення
![]() в попередній формулі знаходиться в
межах [-1,1]) , де
в попередній формулі знаходиться в
межах [-1,1]) , де
![]() – фазова швидкість хвилі в цьому
середовищі. А в напрямку осі (-Z)
поле являє собою стоячу хвилю , так
як
– фазова швидкість хвилі в цьому
середовищі. А в напрямку осі (-Z)
поле являє собою стоячу хвилю , так
як
![]() .
.
В другому середовищі: ![]() ,
,
де
![]() .
Тобто з віддаленням від поверхні розділу
поле експоненціально зменшується.
Швидкість зменшення збільшується із
зростанням
.
Тобто з віддаленням від поверхні розділу
поле експоненціально зменшується.
Швидкість зменшення збільшується із
зростанням
![]() та величини
та величини
![]() .
.
6.3. Граничні умови на поверхні розділу діелектрик-метал
На відміну від звичайних граничних
умов, що зв’язують значення складових
поля на границі розділу в різних
середовищах, граничні умови Щукіна–Леонтовича
виражають зв’язок між складовими
векторів
![]() і
і
![]() в одному середовищі.
в одному середовищі. 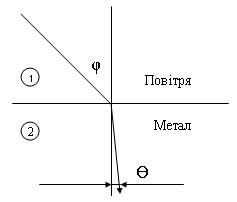 Немагнітний
метал
Немагнітний
метал
![]() являє для електромагнітної хвилі дуже
густе оптичне середовище , в якому модуль
показника заломлення:
являє для електромагнітної хвилі дуже
густе оптичне середовище , в якому модуль
показника заломлення:
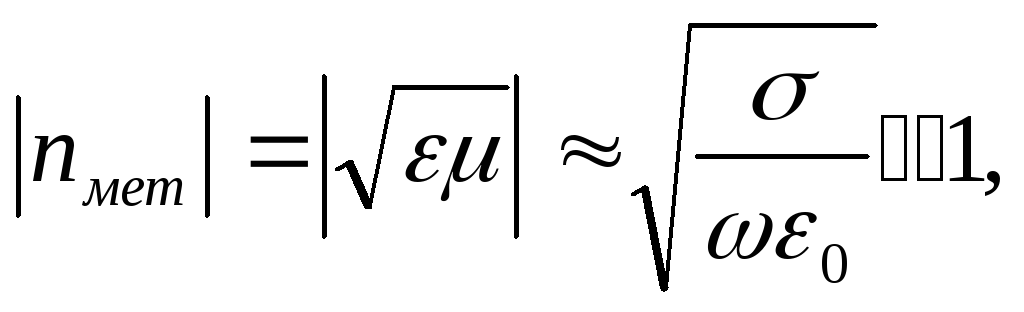 через це з
через це з
![]() виходить , що на
межі розділу повітря-метал (див. рис.)
кут заломлення:
виходить , що на
межі розділу повітря-метал (див. рис.)
кут заломлення:
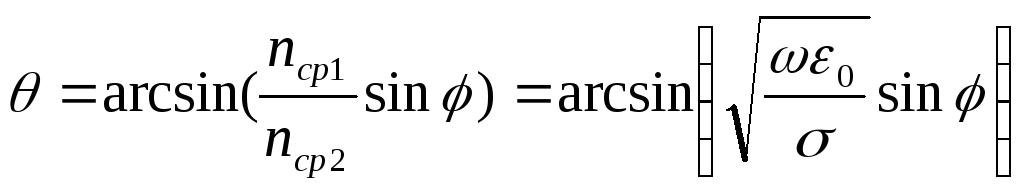 .
(6.18)
.
(6.18)
Незалежно від кута падіння
![]() кут заломлення близький до 0, тобто е/м
хвиля поширюється в металі майже по
нормалі до його поверхні. Дотичні
складові електричного і магнітного
полів на поверхні розділу неперервні:
кут заломлення близький до 0, тобто е/м
хвиля поширюється в металі майже по
нормалі до його поверхні. Дотичні
складові електричного і магнітного
полів на поверхні розділу неперервні:
![]() .
.
Так як кут заломлення любих хвиль при переході розділу діелектрик-метал близький до нуля, тому для довільного поля в діелектрику має місце рівність:
![]() ,
(6.19)
,
(6.19)
де
![]() – орт нормалі, спрямований в метал;
– орт нормалі, спрямований в метал;
![]() – поверхневий опір;
– поверхневий опір;
![]() – називають глибиною проникнення
.
– називають глибиною проникнення
.
Вираз (6.19) є гранична умова Щукіна – Леонтовича.
Граничні умови Щукіна–Леонтовича
справедливі , якщо радіус кривизни
![]() .
На межі метал – діелектрик протікає
поверхневий струм:
.
На межі метал – діелектрик протікає
поверхневий струм:
![]() .
(6.20)
.
(6.20)
Для ідеального провідника:
![]() ,
,
тому виходить, що
![]() а на його поверхні виконуються граничні
умови:
а на його поверхні виконуються граничні
умови:
![]() (6.21)
(6.21)
