
- •Оскільки основа логарифма дорівнює основі системи числення, для перевірки правильності розрахунків можна визначити всі можливі комбінації двійкового коду довжиною 4 біта:
- •Як видно, обидва варіанти рішення дали однаковий результат. Кількісна оцінка інформації в системах з нерівномірним розподілом імовірностей
- •Оцінка недовантаження та надлишковості повідомлень
- •Згідно з формулою (3.1) визначаємо абсолютне недовантаження двійкового шестирозрядного повідомлення:
- •Основи перешкодостійкого кодування. Оцінка перевіряючої та корегуючої здатності кодів
- •Паритетні коди. Кодування за парністю та непарністю повідомлень і блоків даних
- •Код Хеммінга
Основи перешкодостійкого кодування. Оцінка перевіряючої та корегуючої здатності кодів
Приклад 5.1. Визначити мінімальну кодову відстань для коду, що складається з кодових комбінацій: 010101; 101011; 000111.
Розв’язок.
Для визначення мінімальної кодової відстані коду необхідно обчислити значення кодових відстаней, визначених попарним перебором всіх кодових комбінацій коду, тобто для пар кодових комбінацій: 010101 та 101011; 010101 та 000111; 101011 та 000111.
Обчислюємо кодову відстань для кодових комбінацій 010101 та 101011:
010101
101011
111110
d1=1+1+1+1+1+0=5.
Обчислюємо кодову відстань для кодових комбінацій 010101 та 000111:
010101
000111
010010
d2=0+1+0+0+1+0=2.
Обчислюємо кодову відстань для кодових комбінацій 101011 та 000111:
101011
000111
101100
d3=1+0+1+1+0+0=3.
Мінімальну кодову відстань для наведеного коду визначаємо як найменше із значень кодових відстаней d1, d2, d3, тобто:
dmin = d2 =2 .
Приклад 5.2. Визначити перевіряючу та корегуючу здатність коду, наведеного в прикладі 5.1.
Розв’язок.
В попередній задачі нами було визначено мінімальну кодову відстань для коду, значення якої дорівнює 2.
Для визначення перевіряючої здатності коду скористаємось формулою (5.1). З (5.1) отримуємо:
r = dmin –1 = 2-1 =1 .
Таким чином код може виявляти лише одну помилку.
Для визначення перевіряючої здатності коду скористаємось формулою (5.2). Отримуємо:
s = 0.5( dmin –1) = 0.5(2-1) = 0.5 ;
s < 1 .
Таким чином код не спроможний виправляти жодної помилки.
Приклад 5.3. Визначити, скільки контрольних розрядів необхідно додати до шести інформаційних, щоб надати отриманому коду здатність виявляти дві помилки.
Розв’язок.
Кількість контрольних розрядів, які необхідно додати до інформаційних для забезпечення можливості виявлення помилок кратності 2 можна визначити за формулою (5.7), оскільки дві помилки виявляє код з dmin=3, для якого r=2:
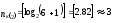
.
Для забезпечення заданої перевіряючої здатності коду до шести інформаційних розрядів необхідно додати три контрольних, тобто, загальна довжина повідомлення буде дорівнювати:
n = ni + nk =6+3 = 9.
Виконаємо перевірку правильності розрахунків за формулою (5.6). При цьому будемо враховувати, що n = 9, та s=1 (для dmin=3 згідно з формулою (5.2)):
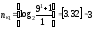
.
Паритетні коди. Кодування за парністю та непарністю повідомлень і блоків даних
Приклад 6.1. Закодувати повідомлення 010101, використовуючи метод кодування:
а) за парністю;
б) за непарністю.
Розв’язок.
а) Для того, щоб закодувати повідомлення за парністю, необхідно до нього додати контрольний розряд таким чином, щоб загальна кількість одиниць в кодовій комбінації була парною. Оскільки в повідомленні 010101 значення 1 мають три розряди (непарна кількість), щоб загальна кількість одиниць в кодовій комбінації була парною значення контрольного розряду повинне дорівнювати 1.
Закодоване за парністю повідомлення буде мати вигляд 0101011.
б) Для того, щоб закодувати повідомлення за непарністю, необхідно до нього додати контрольний розряд таким чином, щоб загальна кількість одиниць в кодовій комбінації була непарною. Оскільки в повідомленні 010101 значення 1 мають три розряди (непарна кількість), щоб загальна кількість одиниць в кодовій комбінації була непарною значення контрольного розряду повинне дорівнювати 0.
Закодоване за непарністю повідомлення буде мати вигляд 0101010.
Приклад 6.2. Перевірити повідомлення на наявність помилки, якщо для кодування повідомлень використано метод кодування за непарністю. Отримані повідомлення мають вигляд: 00000; 10101.
Розв’язок.
Для перевірки на наявність помилки повідомлення, закодованого паритетним методом кодування, необхідно підрахувати кількість одиниць в ньому.
В першому повідомлені 00000 кількість одиниць дорівнює 0, тобто, не відповідає вимогам непарності. Робимо висновок, що повідомлення 00000 містить помилку.
В повідомлені 10101 кількість одиниць дорівнює 3, що відповідає вимогам непарності. Робимо висновок, що повідомлення 10101 не містить помилок.
Приклад 6.3. Закодувати за парністю блок даних
0000
1010
1111
1100
Розв’язок.
Виконаємо кодування за парністю блок даних по горизонталі (рядки блоку). Отримуємо наступний результат (додані контрольні розряди підкреслено):
0000 0
1010 0
1111 0
1100 0
Кодування блоку по вертикалі визначає кінцевий результат:
0000 0
1010 0
1111 0
1100 0
1001 0
Приклад 6.4. Для кодування даних було використано метод блочного кодування за парністю. Перевірити блок на наявність помилки та, якщо це можливо, виправити її. Отриманий блок даних має вигляд:
00000
10100
10110
11000
10010
Розв’язок.
Щоб визначити наявність помилки в блоці даних, закодованому методом блочного кодування за парністю, виконаємо повторне кодування отриманого блока за аналогічною методикою (напівжирним шрифтом визначено вихідний блок даних; однією лінією підкреслені контрольні розряди, які були додані при передачі повідомлення; подвійною лінією підкреслені контрольні розряди, які були додані при повторному кодуванні для пошуку помилок):
0000 0 0
1010 0 0
1011 0 1
1100 0 0
1001 0
0100 0
Як видно, додатковий контрольний розряд в третьому рядку та в другому стовпчику дорівнюють 1. Це свідчить про наявність одиночної помилки на їх перетині. В результаті корегування помилки відновлюємо блок даних, що передавався:
0000 0
1010 0
1111 0
1100 0
1001 0
Вихідний блок даних має наступний вигляд:
0000
1010
1111
1100
