1.2.1. Модель Мальтуса одновидової популяції

Розглянемо модель одновидової біологічної популяції. Через позначимо кількість особин у момент часу . Наша мета – вивести закон зміни кількості особин із часом. Для цього, згідно з принципами математичного моделювання, зробимо деякі спрощувальні припущення. А саме: будемо вважати, що дана популяція існує ізольовано й на деякій території розміщена однорідно. Пізніше ми ці припущення дещо послабимо.

Виберемо закон, згідно з яким відбувається розвиток популяцій. За основу візьмемо відомий закон Мальтуса: швидкість зміни популяції пропорційна величині популяції з певним коефіцієнтом, що є різницею між коефіцієнтом народжуваності і смертності . За цих припущень можна отримати закон зміни чисельності популяцій, що в математичній формі має вигляд

. (2.1.5)

З формули (2.1.5) можна зробити висновки про зміни чисельності з часом. Так, якщо (миттєва народжуваність більша за миттєву смертність), то при ; якщо , то – чисельність із часом не змінюється; якщо – чисельність популяції прямує до нуля.

З математичного погляду дана модель є дуже зручною, оскільки її можна повністю дослідити. Зокрема, з неї випливає результат, який ще у 1798 р. отримав Мальтус і запропонував свою “похмуру теорію”: людство може вижити, тільки якщо періоди зростання в геометричній прогресії будуть перериватися епідеміями, війнами й стихійними лихами. Дійсно, це той випадок, коли і при . Насправді це не так. Модель Мальтуса дуже наближено відповідає оригіналу, коли інтервали часу є невеликими. Її можна розглядати лише як перше наближення до реального процесу.

Дуже складний процес зміни чисельності населення, залежний до того ж від свідомого втручання самих людей, не може описуватись простими законами. Навіть в ідеальному випадку ізольованої біологічної популяції запропонована модель не відповідає реальності повною мірою хоча б через обмеженість ресурсів, необхідних для її існування. З цього випливає так званий ефект насичення.

Вправа. За яких умов на і є:

1. обмеженою при ;

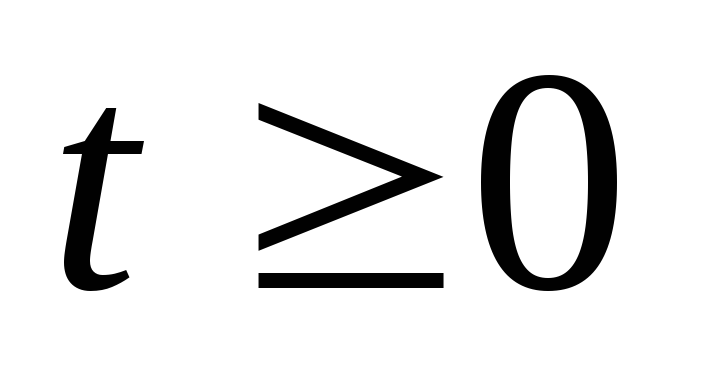2. періодичною?

1.2.2. Модель одновидової популяції з урахуванням насичення (логістична модель)

Більш точна модель має враховувати конкурентну боротьбу в обмеженому життєвому просторі. Зробимо відносно моделі таке припущення, що підтверджується практичними спостереженнями: середньостатистична кількість попарних сутичок у популяції за одиницю часу пропорційна . Тоді рівняння балансу “зміна кількості” = “приріст” – “втрати” можна подати у вигляді

. (2.1.6)

Це рівняння вивів у 1837 р. данський учений Ферхюльст. Воно називається логістичним і є математичною моделлю одновидової популяції з урахуванням ефекту насичення.

Проаналізуємо дану математичну модель. Основна вимога до неї – досить точно описувати реальний процес за великих значень . З математичного погляду цій вимозі відповідає нелінійне рівняння Ріккатті, загальний розв’язок якого може бути знайденим у квадратурах шляхом його зведення до лінійного. Однак точні формули виявляються досить громіздкими для практичного користування. Проте нас цікавить лише асимптотична поведінка розв’язків при . Таке дослідження у випадку, коли і є сталими, можна провести й без інтегрування рівняння (2.1.6).

Заміною змінних і рівняння (2.1.6) можна звести до вигляду

, (2.1.7)

тобто коефіцієнти і можна вважати рівними 1.

Розв’язки залежать від зміни знаків функції . Очевидно, що при і при (нас цікавить випадок ).

Отже, дане рівняння має два положення рівноваги: і , причому перше з них є нестійким, а друге – асимптотично стійким, усі розв’язки при наближуються до нього. Поведінку інтегральних кривих зображено на рис. 2.1.1.

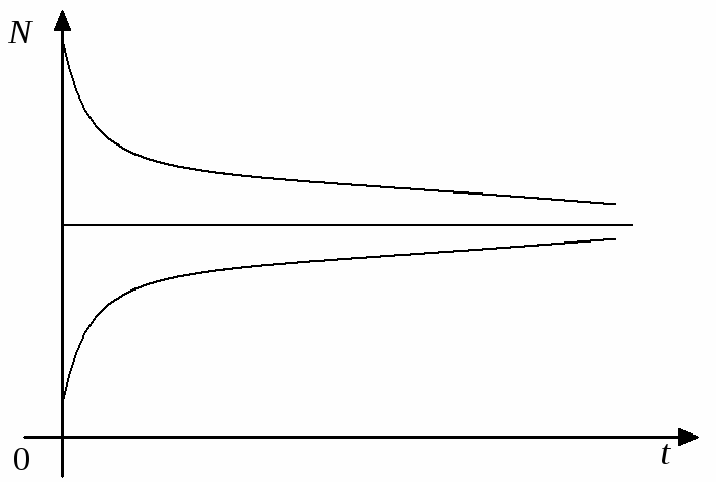
Рис. 2.1.1

Отже, у логістичній моделі всі розв’язки з часом прямують до рівноважного стану, і ніякого перенаселення, як стверджував Мальтус, бути не може.