
- •Блаженков в.В., д.Т.Н., профессор, заведующий кафедрой «Математики» Военной академии рвсн им. Петра Великого.
- •Шеметов в.В., д.Э.Н., профессор, заведующий кафедрой «Менеджмента и маркетинга» Российской Академии предпринимательства. Содержание
- •Предисловие
- •Цель и задачи курса
- •Содержание основных тем программы
- •Парная регрессия
- •Множественная регрессия
- •Реализация типовых задач на персональном компьютере.
- •Рекомендуемая литература.
- •Контрольные вопросы для проверки знаний студентов.
- •Контрольная работа по дисциплине «Эконометрика»
Множественная регрессия
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Рассматривается два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Факторы должны быть количественно измеримы и не дублировать друг друга. Студент должен уметь составлять и анализировать матрицу парных коэффициентов корреляции. Наиболее проста в интерпретации и доступна для вычислений модель множественной линейной регрессии.
Условия Гаусса – Маркова имеют следующий вид:
-
yt = 1 xt1 + 2 xt2 +…+ kxtk + t ;
t = 1… n – спецификация модели.
-
xt1… xtk – детерминированные величины.
-
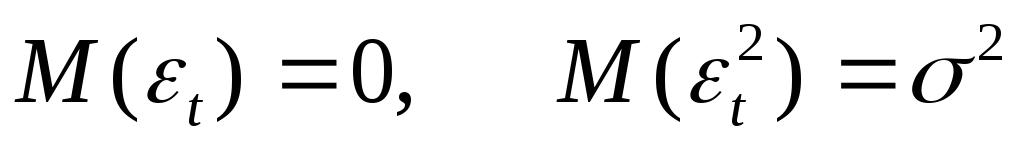 -
не зависят от t.
-
не зависят от t. -
 .
. -
 ~
N(0,2).
~
N(0,2).
Удобна запись в матричном виде.

Тогда для нормальной линейной регрессионной модели:
-
Y = X +
-
X – детерминированная матрица с максимальным рангом k.
-
М() = 0; М ( т) = 2 En - матрица ковариаций.
-
~ N(0, 2 En)
Выборочной оценкой этой модели является уравнение:
![]() ,
где
,
где

Для определения МНК-оценок используем условие:
![]()
Решением является вектор а = (ХТХ)-1 XТ Y
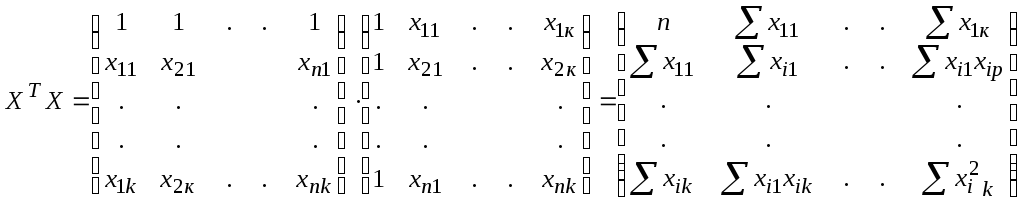
 .
.
Вариации оценок параметров определяют точность уравнения множественной регрессии.
Выборочная оценка ковариационной матрицы
Cov (a) = S2 (XT X)-1, где
S2 – выборочная остаточная дисперсия,
![]() .
.
Оценка
дисперсии коэффициента регрессии
![]() является диагональным элементом матрицы
cov(a).
Значимость аi
определяется по t-критерию
путем сравнения с tкр
(1-;
n-k-1).
является диагональным элементом матрицы
cov(a).
Значимость аi
определяется по t-критерию
путем сравнения с tкр
(1-;
n-k-1).
Коэффициент
детерминации
![]() .
.
Значимость уравнения в целом проверяется исходя из F-критерия.

Если модель адекватна и точна, то возможен прогноз.
y (n+k) = yp(k) u(k), где
![]()
Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий применяют средние частные коэффициенты эластичности
![]()
и
![]() - коэффициенты:
- коэффициенты:
![]() .
.![]()
Коэффициент
эластичности показывает, на сколько
процентов изменится зависимая переменная
при изменении фактора j
на 1%. Бета-коэффициент показывает, на
какую часть величины среднего
квадратического отклонения
![]() y
изменится зависимая переменная Y
с изменением Х на величину своего
среднеквадратического отклонения при
фиксированном на постоянном уровне
значения остальных независимых
переменных.
y
изменится зависимая переменная Y
с изменением Х на величину своего
среднеквадратического отклонения при
фиксированном на постоянном уровне
значения остальных независимых
переменных.
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов:
![]() где
где
r (j) – коэффициент парной корреляции между фактором и зависимой переменной.
Рассмотрим известный пример:
Бюджетное обследование пяти случайно выбранных семей дало следующие результаты:
|
Семья |
Накопление, S |
Доход, Y |
Имущество, W |
|
1 |
3 |
40 |
60 |
|
2 |
6 |
55 |
36 |
|
3 |
5 |
45 |
36 |
|
4 |
3,5 |
30 |
15 |
|
5 |
1,5 |
30 |
90 |
Истинная модель: S = 0 + 1Y + 2W +
Оцененная
модель:
![]() = X
a
= X
a
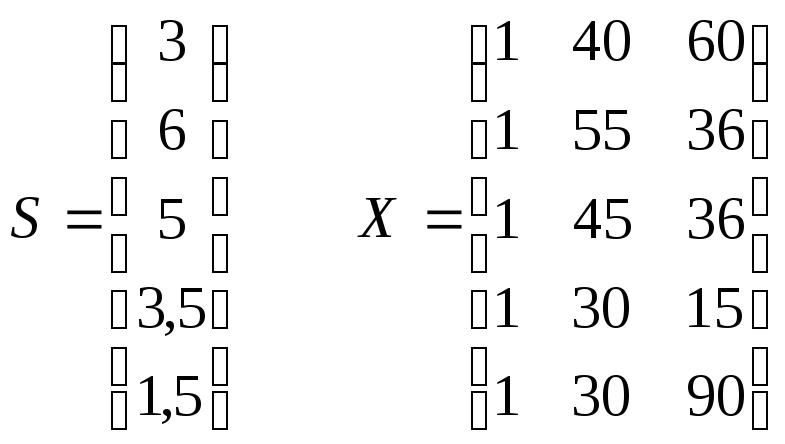
Вычислим:

Отметим, что обратную матрицу удобно находить, используя преобразования Жордана-Гаусса.
В итоге
 ,
,
Оцененная модель:
![]()
Интерпретация модели:
-
изменение дохода на 1 единицу приведет к увеличению накопления на 0,12 единиц;
-
увеличение стоимости имущества на 1 единицу приведет к уменьшению накопления на 0,03 денежных единиц.
ESS
=
(S-![]() (S-
(S-![]() =
0,281, df1
= 2.
=
0,281, df1
= 2.
RSS
= (![]() -
-![]() =
12,019, df 2=
2.
=
12,019, df 2=
2.
![]() -
97% изменения накопления объясняются
моделью, 3% - неучтенными факторами.
-
97% изменения накопления объясняются
моделью, 3% - неучтенными факторами.
![]() =
42,75
=
42,75
Fкр (0, 05; 2; 2) = 19; Fнаб >Fкр, уравнение признается значимым в целом.
![]() ,
,
Cov (a) = S2 (XT X)-1;
![]() 0,
80
0,
80
![]()
![]()
![]()
![]()
![]()

Отметим, что несмотря на то, что а0 незначим (tH < tкр), уравнение, исходя из F-критерия в целом значимо.
Пусть некоторая семья имеет доход Y = 30 и имущество W = 52,5.
Определим
прогнозное значение накоплений. Для
шестой семьи
 .
.
![]()
![]()
![]()
В предположении, что для шестой семьи выявленная тенденция сохранится, 95%-й доверительный интервал будет иметь следующий вид:
![]()
![]()
Верхняя граница прогноза - 8,83 усл. ден.ед.
Нижняя граница прогноза – 3,93 усл. ден.ед.

Составим вспомогательную таблицу:
|
|
|
|
|
|
|
-0,8 |
0 |
12,6 |
0 |
-10,08 |
|
2,2 |
15 |
-11,4 |
33 |
-25,08 |
|
1,2 |
5 |
-11,4 |
6 |
-13,68 |
|
-0,3 |
-10 |
-32,4 |
3 |
9,72 |
|
-2,3 |
-10 |
42,6 |
23 |
-98,00 |
|
Итого |
0 |
0 |
65 |
-137,12 |
![]()
![]() ;
;
![]()
