1. Провести прямую через две заданные точки () и ().

В качестве направляющего вектора прямой, возьмем вектор

= = ( ).

Тогда коэффициентами общего уравнения при переменных будут A=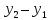 и B= (). Если за исходную точку при построении уравнений прямой выбрать , то ее параметрические уравнения

,

каноническое уравнение

,

общее уравнение

.

Пример. Провести прямую 𝑙 через точки (1, 1) и (2, 3). Условия задачи знаками математической стенографии записываются так: ∊𝑙⋼. Здесь искомый объект помещен в середину записи и окаймлен исходными данными.

Поскольку ==(3, 2), то сразу же можно записать 2x+3yС=0.

Свободный член уравнения, как и ранее, найдем из условия прохождения прямой линии через заданные точки. Подставив в уравнение координаты точки , найдем С=5. В итоге получаем 𝑙: 2x+3y5=0. Подстановкой убеждаемся, что заданные точки действительно удовлетворяют построенному уравнению и потому лежат на искомой прямой.

Упражнение. Проверить, что выбор в качестве исходной точки вместо , а вместо вектора ему противоположного  приведет к тому же самому результату.

2. Провести прямую через точку (, ), параллельно заданной прямой 𝑙: Ax+By+C=0 (∊‖𝑙).

У параллельных прямых как направляющие векторы, так и нормали коллинеарны. Поэтому в качестве нормали искомой прямой может быть принята нормаль заданной прямой =(A,B). Тогда общее уравнение искомой прямой записывается в виде Ax+By+D=0, в котором неизвестна только константа D. По условию задачи A+B+D=0. Выражая из этого равенства D и подставляя его в предыдущее уравнение, окончательно находим

.

Пример. Найти уравнение прямой : (1,2) ∊ ‖ l: x+2y+3=0. Подставляя в формулу численные значения, получаем : x+2y5=0.

3. Провести прямую 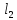через точку (, ), перпендикулярно заданной прямой l: Ax+By+C=0 (∊⊥𝑙).

В качестве нормального вектора искомой прямой может быть принят направляющий вектор заданной прямой , т.е. ==(B,A). Тогда данная задача решается аналогично предыдущей, и в итоге получаем

.

Пример. Построить уравнение прямой : (1, 1) ∊ ⊥𝑙: xy1=0.

Подстановка исходных данных в расчетную формулу дает : x+y2=0.

4.4. Взаимное расположение прямых. Геометрическая

интерпретация решения системы линейных уравнений

Сначала исследуем возможное расположение прямой относительно осей координат.

I. Прямая 𝑙 параллельна оси абсцисс, тогда ‖, а ‖. Это означает, что =λ=λ(0, 1)=(0, λ). Вспомнив, что координаты нормального вектора являются коэффициентами общего уравнения прямой, т.е. А=0 и В=λ находим 𝑙: B𝑦+C=0 или y = C/B.

2. Прямая 𝑙 параллельна оси ординат, тогда ‖ . Аналогично

предыдущему случаю =λ=λ(1, 0)=(λ, 0). Теперь, обозначив А=λ и В=0, получаем 𝑙: Aх+C=0 или х = C/A.

3. Прямая проходит через начало координат. Подставляя в общее уравнение прямой координаты начала (0, 0), находим С=0. Тогда общее уравнение прямой будет иметь вид Aх+ By=0 или y=(A/B)𝑥.

4. Общий случай A≠0, B≠0, C≠0 означает прохождение прямой не через начало координат под не прямыми углами к осям абсцисс и ординат.

При наличии двух произвольных прямых закономерно возникает вопрос об оценке их взаимного расположения. Анализ возможных ситуаций произведем с помощью общего уравнения прямой в терминах направляющих и нормальных векторов.

Итак, пусть две прямые заданы общими уравнениями

, =(, ), =(,),

, =(,), =(,).

Исследование взаимного расположения двух прямых предполагает анализ их уравнений, объединенных в одну систему

5. Единственности решения такой системы соответствует пересечение прямых в одной единственной точке, что будет иметь место только в случае не коллинеарности их направляющих (нормальных) векторов.

Условие ∦ означает непропорциональность соответствующих координат этих векторов, т.е.

или ≠0.

Для решения системы достаточно применить метод Гаусса, который вычислит координаты точки пересечения прямых, т.е. их общую точку.

6. В случае пропорциональности всех коэффициентов

= = λ

первое уравнение получается из второго умножением на некоторое число. Тогда реально имеется, по сути дела, одно-единственное уравнение, т.е. одна прямая. Однако эта ситуация формально интерпретируется как наложение двух прямых. Выражая из первого уравнения одну переменную через другую, находим зависимость

y= x  или x= y  .

Полученный результат означает, что придавая одной переменной некоторое значение, для другой переменной получим соответствующее значение. Таким образом, в данном случае решений бесконечно много, как и точек на прямой (неопределенная система).

7. На долю последнего мыслимого случая

≠

остается параллельность прямых (как параллельный сдвиг одной прямой относительно другой на некоторую величину), что означает отсутствие точки их пересечения и, соответственно, отсутствие решения системы линейных уравнений (несовместная система).

Резюмируя вышеизложенное, теперь можно сформулировать признаки совместности, неопределенности и несовместности системы линейных уравнений и дать геометрическую интерпретацию этих ситуаций через взаимное расположение соответствующих прямых.

Система двух линейных уравнений c двумя неизвестными:

 имеет единственное решение в случае непропорциональности

коэффициентов при переменных (прямые пересекаются);

 имеет бесконечно много решений в случае пропорциональности всех

соответствующих параметров уравнений (наложение прямых);

 не имеет решения в случае пропорциональности коэффициентов и

непропорциональности свободных членов (прямые параллельны).

Примеры.

x

Прямые 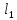и построим по точкам

их пересечения с осями координат.

Единственное решение означает

пересечение двух прямых.

5. Методы условной оптимизации

5.1. Краткая история и суть вопроса

В середине прошлого века начало интенсивно развиваться научно-прикладное направление, получившие название "Исследование операций" (ИО), занимающееся изучением систем различной природы с помощью методов математического моделирования. Результатом применения методов ИО является выработка рекомендаций по проектированию и изменению систем с целью повышения эффективности их функционирования в соответствии с определенными требованиями и реальной обстановкой. Этот раздел посвящен изучению объектов, эффективность функционирования которых оценивается некоторым критерием. Например: минимум затрат, максимум прибыли, минимум отходов, минимум затраченного времени и т.п. При этом реальная обстановка учитывается некоторой совокупностью ограничений на допустимые изменения параметров объекта. В результате такого подхода математическая модель исследуемого объекта формализуется в виде задачи условной оптимизации. По сути дела, назначение любой оптимизационной модели заключается в том, чтобы, располагая ограниченными возможностями, обеспечить достижение максимального эффекта, иными словами  из сложившейся реальной ситуации извлечь максимум желаемого.

При условии адекватности математической модели (соответствия моделируемому объекту) расчеты по ее компьютерному аналогу позволяют выявить практически важные и далеко не очевидные аспекты функционирования исходного объекта  оригинала.

В планировании и управлении чем выше ставки, тем более жесткие требования предъявляются к бизнес-планам. Поэтому при обосновании принимаемых решений математические методы играют исключительно важную роль. Одним из таких методов является математическое программирование (МП). Под названием МП объединяется целая группа методов условной оптимизации, и в их числе  линейное программирование (ЛП), представляющее собой наиболее простую модель оптимального использования ограниченных ресурсов с линейным критерием эффективности и системой условий, выраженной линейными неравенствами.

В рамках моделей ЛП решается немало задач, в том числе не линей- ных, но допускающих линеаризацию соотношений с достаточно высокой степенью точности. Вследствие широкой применимости ЛП составляет в практических приложениях целое направление. Его основоположникам, в числе которых есть и наш соотечественник – академик Л.В. Канторович, в 1975 г. была присуждена Нобелевская премия. А это, как известно, является высшей формой всемирного признания научной и практической значимости достижений в любой области.

Для понимания методологических и алгоритмических основ ЛП достаточно материала настоящего пособия, изложенного к настоящему моменту. Ввиду относительной простоты ЛП и возможности наглядной графической иллюстрации хода решения задач внимание будет сосредоточено именно на этом методе оптимизации.

5.2. Постановка задачи линейного программирования

Для конкретности проанализируем функционирование фирмы, которая занимается производством и реализацией продукции хлебобулочной продукции. Пусть ежедневно выпекаются изделия n видов: батоны, бублики, пряники, печенье и др. При этом используется m ингредиентов: мука, соль, сахар, молоко, масло, яйца, изюм, кунжут, и т.п. Причем в калькуляциях каждого предприятия заложены нормы расхода сырья и прибыли по всем видам продукции. В дальнейшем виды продукции будем индексировать символом j, а сырье  i. Таким образом, известно, что на изготовление 1 кг j-й продукции расходуется кг i-го сырья, общее количество которого ограниченно величиной . Прибыль от реализации продукции также в расчете на 1 кг, обозначим . Исходные данные исчерпываются перечисленными выше показателями.

В условиях реального производства естественным является стремление спланировать выпуск продукции с таким расчетом, чтобы обеспечить максимум прибыли, разумеется, с учетом действующих ограничений по сырью. Для полноты следовало бы ввести в рассмотрение ограничения по производственным мощностям с учетом использования одного и того же механизма при изготовлении разных видов продукции. Однако это привело бы к существенному усложнению модели.

Обозначим  объем выпуска j-й продукции в кг. Тогда на этот объем придется прибыль в размере , а совокупная прибыль по всем видам продукции составит

L() = .

Расход i-го сырья при изготовлении j-й продукции в объеме равен , а в общей сложности оно будет израсходовано в количестве . Суммирование изложенных выше фактов в соответствии с принятой терминологией приводит к формулировке следующей задачи оптимального планирования

,

ЦФ  целевая функция КО  критерий оптимальности

≤

система ограничений (СО)

или система условий (СУ).

Последние неравенства выражают неотрицательность переменных как объемов производства. Таким образом, сформулирована задача оптимизации плана производства продукции на максимум прибыли при ограниченных ресурсах.

В период реконструкции производства или в момент материальных затруднений разумным тактическим ходом является такое снижение объемов производства, которое позволило бы хоть и с потерями, но сохранить за собой в будущем занимаемый сектор рынка. Данной ситуации отвечает задача минимизации совокупной себестоимости произведенной продукции при поддержании производства на уровне не ниже заданного:

⟶ min ,

Здесь  показатели удельной себестоимости продукции, а  минимально допустимый уровень удовлетворения спроса.

Формализация связи параметров объекта (безотносительно к их экономическому содержанию) в форме линейных соотношений, представленных целевой функцией, критерием оптимальности и системой ограничений, называется задачей линейного программирования (ЛП). Суть задачи ЛП заключается в поиске решения, наилучшего в смысле принятого критерия оптимальности. Набор значений переменных, удовлетворяющих всем ограничениям, называется допустимым решением или планом. Совокупность допустимых решений задачи ЛП образует геометрическую фигуру М, называемую "многогранником допустимых решений". Допустимое решение, доставляющее оптимум ЦФ на М, называется оптимальным и обозначается

=(), = opt .

x∊M

5.3. Дробно-линейное программирование

Немалый практический интерес представляет наиболее эффективное использование денежных средств, выражаемое показателем рентабельности, играющим в экономике весьма важную роль. Данный показатель исчисляется отношением прибыли к себестоимости и характеризует величину прибыли, приходящуюся на единицу затрат, т.е. отдачу с одного рубля. Экономическое содержание рентабельности предопределяет стремление увеличивать ее по мере возможности. Применительно к рассмотренному выше примеру целевая функция задачи на максимум рентабельности будет дробно-линейной

⟶ max,

Сообразно этому обстоятельству такая задача называется дробно-линейной. Чисто формальным приемом ввода новых переменных

=1/ и =

соответствующим преобразованием ЦФ и умножением неравенств системы ограничений на дробно-линейная задача сводится к линейной:

⟶ max ,

Дополнительное условиеравенство в системе ограничений возникает в результате следующих преобразований

=1/ ⇒ =1 ⇒ =1 ⇒ =1.

В довершение ко всему сохраняется не отрицательность переменных. После решения задачи по найденным значениям переменных восстанавливается оптимальный план исходной задачи = /, Таким образом, использованная замена переменных является вполне конструктивной.

5.4. Транспортная задача

Важный класс задач линейного программирования представляет так

называемая транспортная задача. При планировании перевозок грузов естественным образом возникает стремление минимизировать транспортные расходы. Транспортная задача формулируется следующим образом.

Имеется p баз, в которых находится единиц однородного продукта и q потребителей с потребностями в этом продукте. Стоимость перевозки единицы груза из i-го пункта j-му потребителю равна . Составить схему перевозок с минимальными транспортными расходами при условии сбалансированности спроса и потребления. Обозначим количество единиц груза, перевозимого из i-го пункта j-му потребителю. Суммарные транспортные затраты подлежат минимизации с учетом наличных запасов и потребностей:

⟶ min ,

Здесь первое условие в системе ограничений означает полное удовлетворение потребностей, а второе – полное использование запасов. В итоге имеем строгий баланс потребностей и запасов , при котором транспортная задача всегда имеет решение.

Рассмотренная выше простейшая однопродуктовая транспортная модель может быть расширена до многопродуктовой. Кроме того, множество практических задач органично содержит транспортную составляющую. Применительно к примеру с пекарнями это может выглядеть следующим образом. Фирма располагает рядом пекарен и точек реализации произведенной продукции, которую развозит на своем транспорте. Требуется найти оптимальную схему прикрепления магазинов к пекарням, обеспечивающую минимум транспортных расходов. Поскольку в данном случае производитель сам же занимается и транспортировкой свой продукции, то целесообразно объединение производственной и транспортной составляющих в рамках одной модели минимизации суммарных производственных и транспортных затрат с учетом действующих ограничений.

Симбиоз производственной и транспортной составляющих в рамках одной модели может быть реализован следующим образом. Заметим, что максимизация целевой функции L эквивалентна минимизации противоположной по знаку функции –L. По этой причине представляется возможным формирование гибридной целевой функции, в которой производственный сектор представлен показателем суммарной прибыли, взятым с обратным знаком, а транспортная составляющая содержит транспортные расходы. Обе эти компоненты целесообразно взять с весовыми коэффициентами, составляющими в своей сумме единицу. В результате критерий оптимальности "min" обеспечит максимальный совокупный эффект при определенной сбалансированности интересов производственной и транспортной составляющих. С помощью весовых коэффициентов можно варьировать интересами соответствующих секторов, склоняя их по своему усмотрению в ту или иную сторону.

5.5. Математическое программирование

Если речь идет о производстве дорогостоящих изделий или о выборе стратегии поведения системы из некоторого множества возможностей (нулевое значение переменной означает отклонение соответствующей стратегии, а единица – её принятие), то дробный ответ устроить никак не может. В этом случае на переменные налагается дополнительное требование целочисленности. Такие задачи являются предметом целочисленного программирования, методы которого по сравнению с ЛП являются более сложными.

В реальных условиях соотношения оптимизационной задачи нередко оказываются существенно нелинейными. В общем случае целевая функция и система ограничений выражаются некоторыми функциями. Такие задачи решаются методами нелинейного программирования.

Отдельный класс составляет нелинейные задачи, являющиеся по своей сути многошаговыми, с последовательным принятием на каждом шаге решений, обеспечивающих оптимальное развитие некоторой начальной ситуации. Решением таких задач занимается динамическое программирование (ДП). Несмотря на то, что методология ДП находится за пределами настоящего курса, стоит привести её основу, известную под названием «принцип оптимальности Беллмана», который формулируется следующим образом: каково бы ни было начальное и текущее состояние системы перед очередным шагом (этапом) планирования, все последующие решения должны обеспечивать максимальный эффект (выигрыш) относительно состояния, сложившегося в результате решений, принятых на предыдущих шагах. Этот принцип позволяет построить алгоритм численного решения многошаговой задачи в виде рекуррентных соотношений. Кроме того, он представляет собой по сути дела руководство к действию в многошаговых процедурах принятия решений даже на интуитивном уровне, конечно, при наличии возможности хотя бы оценить последствия принимаемых решений.

Стратегический многолетний план развития объекта складывается из последовательности этапов, на каждом из которых обозначаются тактические цели. В содержательном отношении эти частные цели и пути их реализации на каждом этапе могут отличаться друг от друга самым существенным образом. В то же время, в своей совокупности они должны быть согласованы между собой в интересах достижения глобальной конечной цели. Грамотное решение задачи согласования обеспечивает применение методологии системного анализа.

Принцип оптимальности Беллмана находится в полном соответствии с практикой планирования и функционирования реальных систем.

В самом деле, в процессе деятельности системы обстановка может меняться самым непредвиденным образом, вследствие чего коррекция планов становится неизбежной. Поэтому, находясь в условиях постфактум, в начале каждого шага разумно обеспечить оптимальное развитие последующих состояний системы все зависимости от её предыстории.

Реалии бизнеса таковы, что, несмотря на наличие планов на перспективу, их реализация осуществляется поэтапно с корректировкой решений на последующую часть планового периода по мере поступления информации о фактических достижениях. При этом рынок по сути дела является противодействующей стороной с неясной и неоднозначной реакцией, что порождает неопределенность условий функционирования объекта. Такие задачи составляют предмет стохастического многошагового программирования и многошаговых игр, а также интенсивно развивающейся в последнее время методологии нечеткой логики и нейронных сетей.

Изменение исходных данных может существенно повлиять на предсказываемое поведение объекта. Если сравнительно малым изменениям исходных данных отвечают малые изменения конечных результатов, то такая модель называется устойчивой. Устойчивость модели относительно возмущения исходных данных повышает надежность выводов и в этом смысле является безусловно положительным качеством.

Рассмотренные выше обстоятельства ничуть не умоляют достоинств ЛП, которое с успехом применяется при решении большого числа практических задач. Поэтому в дальнейшем мы ограничимся изучением ЛП, образующего обширный и в то же время наиболее доступный для понимания класс линейных экономико-математических моделей.

В заключение следует отметить, что в своей деятельности мы стараемся принимать решения, следуя именно принципу оптимальности  с наибольшей для себя выгодой. Другое дело, что в силу различных причин достигать оптимальности удается далеко не всегда. Однако это ничуть не снижает практической значимости оптимизационных задач.

5.6. Геометрические аспекты линейного программирования

Часть плоскости по одну сторону от прямой линии называется полуплоскостью, т.е. прямая делит плоскость на две полуплоскости. Каждое линейное неравенство обращается в равенство на прямой линии. Неравенство ">" выполняется в той полуплоскости, на которую указывает нормальный вектор прямой. В другой полуплоскости действует противоположное неравенство "<". Для доказательства возьмем неравенство вида . Множеству точек, для которых имеет место равенство, отвечает прямая l: с нормальным вектором . Возьмем точку прямой , т.е. и сместимся из нее вдоль нормали на некоторую величину, что может быть выражено так

→ () + t = () + t = (), .

Подставив координаты полученной таким образом точки в левую часть уравнения прямой, найдем, что для любого t >0

+=.

Таким образом, неравенство ">" справедливо по ту сторону прямой, т.е. в той полуплоскости, на которую ориентирован ее нормальный вектор. Каждому ограничению задачи ЛП с двумя переменными отвечает своя полуплоскость, в которой оно выполняется. Множество точек М, где справедливы все ограничения задачи, как общая часть всех полуплоскостей представляет собой выпуклый многоугольник (вместе с любыми двумя своими точками содержит весь соединяющий их отрезок).

В дальнейшем пригодится то обстоятельство, что по аналогичной причине направление возрастания линейной целевой функции указывает вектор, составленный из её коэффициентов (нормальный вектор).

В теории ЛП доказывается, что в многомерном случае (аналогично плоскости) множество М представляет собой выпуклый многогранник допустимых решений (МДР), а оптимум целевой функции достигается, по крайней мере, в одной из его вершин. Эта вершина вычисляется как решение соответствующей системы линейных уравнений, взятых из системы ограничений как равенства. Достижение оптимума возможно не только в одной вершине, но и на целом ребре (отрезке, соединяющем две смежные вершины) или даже грани М, и тогда задача имеет бесконечно много решений. Несовместность системы условий задачи означает отсутствие хотя бы одной вершины многогранника допустимых решений (М – пустое множество). В системе условий задачи, возможно, имеются несущественные, т.е. те, которые могут быть исключены без всякого ущерба.

Вот собственно и все основные сведения, которых в совокупности с изложенным ранее материалом вполне достаточно для решения приведенной ниже простой задачи ЛП на плоскости:

L() = ⟶ max ,

Задачу ЛП с двумя переменными можно решить геометрическим методом, который реализуется следующим образом: строится многогранник

допустимых решений М; находятся его вершины как пересечения соот-

ветствующих прямых; путем перебора вершин определяется та, в которой достигается максимум целевой функции. Выявление областей выполнения неравенств произведем на примере ограничения (II). Для этого вспомним, что у прямой нормальный вектор . Поскольку он использу-ется исключительно в качестве указателя направления возрастания правой части этого равенства, то его можно строить в произвольно выбранной точке по ранее сформулированному принципу  координаты вектора определяют координаты его концевой точки относительно начала. Для удобства вектор укоротим в шесть раз и построим . Этот вектор указывает на ту часть полуплоскости, где справедливо неравенство . Значит, ограничение (II) как противополож-ное будет действовать по другую сторону прямой. Построенный по такому принципу многоугольник М на рисунке обозначен штриховкой. Его вершины найдены как точки пересечения прямых (отвечающих неравенствам задачи), посредством решения соответствующих систем линейных уравнений. Так неравенства (I) и (IV) создают точку многоугольника М с координатами (2, 1), (III) и (IV) – точку (I, I) и т.д. Однако рассматриваются только те точки, которые удовлетворяют всем остальным ограничениям (помимо тех, которыми они образованы) т.е. являются вершинами М. Например, точка (I, I) вершиной М не является, поскольку не удовлетворяет первому неравенству. Ограничения (V) и (VI) могут быть опущены как несущественные. Из рисунка видно, что многоугольник М насчитывает четыре вершины. Ту из них, в которой достигается максимум целевой функции, найдем сравнением значений ЦФ:

L(2, 1)= 1, L(1, 2)=1, L(1, 36/7)= 29/7≈4.1, L(35/6, 1)= 29/6≈4,8.

Таким образом, ответ: =1, =36/7, = L ()=29/7.

Этот результат можно было получить сразу после построения многоугольника М, если учесть, что он должен целиком располагаться под плоскостью = max. На рисунке изображена прямая L, отвечающая целевой функции, и построен нормальный вектор =(1, 1), указывающий направление возрастания ЦФ. Очевидно, что вершина (1, 36/7) многоугольника М является искомой и дальнейший рост целевой функции на М невозможен, поскольку при любом сколь угодно малом смещении вдоль вектора контакт прямой (ЦФ) с М будет утрачен, а в ЦФ по условию задачи можно подставлять координаты точек только из М.

Заметим, что очевидным следствием исключения из СУ задачи условий (II) и (V) будет неограниченность ЦФ на МДР.

5.7. Симплекс-метод

Среди существующих алгоритмов решения общей задачи ЛП наибольшей известностью пользуется симплекс-метод. Формальная вычислительная схема этого метода в виде симплекс-таблиц (подобно расширенной матрице в методе Гаусса) детально изложена во многих источниках, поэтому ограничимся изучением его содержательной части.

Для лучшего понимания симплекс-метода на идейном уровне рассмотрим решенную ранее геометрическим методом задачу ЛП, опустив несущественные ограничения:

L() = ⟶ max ,

Преобразуем два последних неравенства в условия неотрицательности путем введения новых переменных = и =. В новых

переменных задача примет вид

L() = ⟶ max ,

Введением балансовых переменных и ограничения задачи превращаются в равенства с равноправными неотрицательными переменными:

При этом целевая функция задачи формально может быть записана в виде

L() = + 0 + 0.

Теперь из каждого уравнения выберем по одной переменной, которые будут называться базисными, и выразим их через остальные так называемые свободные переменные. В качестве базисных удобно принять переменные и и тогда и будут свободными:

Полагая свободные переменные не отрицательными и обеспечивающими также неотрицательность базисных переменных, например, =0, =1, найдем начальное допустимое решение =(0, 1, 0, 22), =1. На этом заканчивается подготовительный шаг симплекс-метода.

Первая итерация. ЦФ нашей задачи такова, что ее увеличение возможно только за счет роста переменной при =0. Однако рост 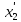ограничивает второе равенство, допускающее в качестве максимального значения =29/7 из расчета обращения в 0. Подставив в уравнения и ЦФ значения свободных переменных, найдем первое допустимое решение

=(0, 29/7, 22/7, 0), = 29/7.

Начиная с этого момента, на каждой итерации в качестве свободных будут приниматься переменные с нулевыми координатами в найденном допустимом решении. Преобразуя в соответствии с этим правилом систему ограничений и целевую функцию, получим сначала

второго уравнения в первое и в ЦФ, найдем

L = .

Вторая итерация. Поскольку все коэффициенты ЦФ отрицательны, то ее дальнейший рост невозможен ни при каких положительных значениях свободных переменных, что свидетельствует об окончании решения задачи. Таким образом, =0, = 29/7 и возвращаясь к исходным переменным, получаем =+1=1, =+1=36/7, = 29/7.

В отличие от системы линейных уравнений проверка правильности решения задачи ЛП в целом является весьма сложной вычислительной процедурой. Прямой подстановкой можно установить лишь то, что найденное решение удовлетворяет системе ограничений задачи. Для проверки оптимальности найденного решения достаточно воспользоваться аппаратом векторной алгебры.

На графической иллюстрации изображена оптимальная вершина многогранника допустимых решений с критерием оптимальности  max. Целевой функции отвечает прямая линия L с нормальным вектором , координатами которого являются коэффициенты этой функции. Для оптимальности вершины необходимо и достаточно чтобы векторы и составляли с вектором угол не менее 90°, что устанавливается с помощью скалярного произведения. Координаты вершин находятся путем решения соответствующих систем линейных уравнений, а координаты векторов вычисляются как разности координат конечной и начальной точек. Изложенный ранее материал вполне достаточен для реализации предложенной здесь схемы проверки оптимальности найденного решения.

При одном взгляде на рисунок очевидна аналогия ситуации максимума с достигшим вершины альпинистом, тело которого (от ног к голове) сориентировано в направлении нормального вектора целевой функции, и всю гору (МДР) он видит целиком под собой внизу.

Приведенный выше численный вариант симплекс-метода без использования симплекс-таблиц годится лишь для задач с двумя-тремя переменными и столь же малоэффективен, как и решение системы линейных уравнений путем прямой замены неизвестной в одном уравнении ее

выражением, полученным из другого уравнения. Этот алгоритм рассматривался исключительно с целью не упустить за формальными расчетами существо механизма поиска оптимума линейной задачи.

Основная идея симплекс-метода заключается в переходе на каждом шаге алгоритма в такую вершину многогранника допустимых решений, чтобы значение целевой функции в смысле критерия оптимальности улучшилось или, по крайней мере, не ухудшилось. Далее процесс циклично повторяется. Содержанием каждой итерации является проверка возможности улучшения значения ЦФ и вычисление следующего допустимого решения путем пересчета коэффициентов системы. По сути дела симплекс-метод является методом последовательного улучшения допустимого решения. В процессе его применения реализуется одна из следующих ситуаций:

 устанавливается факт несовместности системы ограничений;

 вычисляется оптимальное решение задачи и определяется,

единственно оно или нет;

 выявляется неограниченность ЦФ на МДР.

Вычислительная схема симплекс-метода такова. Сначала с помощью балансовых переменных система ограничений задачи ЛП сводится к системе равенств, и заполняется симплекс-таблица, которая подобно расширенной матрице системы линейных уравнений содержит все числовые коэффициенты ЦФ и СО, а также ряд вспомогательных параметров. Затем находится начальное допустимое решение, или выявляется несовместность системы ограничений задачи (М=∅). Весь процесс последующих вычислений представляет собой последовательность итераций, на каждой из которых по определенным правилам происходит преобразование симплекс-таблицы, обеспечивающее последовательное улучшение значения целевой функции до тех пор, пока не будет найдено оптимальное решение задачи или установлена неограниченность целевой функции задачи.

Признаком неограниченности целевой функции на множестве допустимых решений является возможность улучшения её величины при отсутствии ограничений на значения фигурирующих в ней переменных.

Применение симплекс-таблиц обеспечивает эффективное решение задач любой размерности и детально изучается в любом серьезном учебнике, содержащем раздел "Линейное программирование".

Для найденного решения задачи может быть произведен после- оптимизационный анализ результатов расчетов, позволяющий в частности оценивать устойчивость моделей ЛП.

Практикум

При решении задач в меру необходимости применяется логика рассуждений  практически такая же, каковой мы пользуемся в своей повседневной деятельности. Ход решения задач предопределяется исходными данными.

Матрицы

1. Найти сумму матриц

+ = = .

Сложение матриц произведено по известному правилу. Обе слагаемые матрицы являются треугольными (одна  нижняя, другая  верхняя).

2. Умножить матрицу на число

3 = = .

3. Посчитать результат арифметических операций над матрицами

2 = = .

4. Умножить вектор-строку на вектор-столбец

 = 01 + 12 + 2 0 = 2

и вектор-столбец на вектор-строку

 = = .

Эти примеры еще раз демонстрируют не коммутативность произведения матриц, т.е. зависимость результата от порядка сомножителей.

5. Найти произведение двух матриц

= =

= .

Системы линейных уравнений

Решить системы линейных уравнений методом Гаусса

Действуя по методу Гаусса, составим расширенную

матрицу, приведем ее левую секцию к единичной

матрице, в правой секции найдем решение системы.

.

Следует помнить, что на каждой стадии преобразований расширенной матрицы аналогичные действия производятся над соответствующими уравнениями. Поэтому в любой момент каждую строку расширенной матрицы можно прочитать как уравнение, коэффициентами которого являются элементы строки. Поступив так, получим = 2, =3,= 2.

Прямой подстановкой в уравнения нетрудно убедиться в том, что найденные значения неизвестных в самом деле являются решением системы.

.

Нулевая строка свидетельствует о том, что система является неопределенной. Выражая две первые переменные через третью, найдем

Последняя строка, читаемая как уравнение, даст результат "0=2", который может быть истолкован как противоречие. Однако на самом деле это противоречие мнимое. Преобразования метода Гаусса подбирались по принципу сохранения равенств. В случае несовместности системы одновременное выполнение всех равенств невозможно ни при каких значениях переменных, т.е. среди равенств, по крайней мере, одно будет неравенством. Результатом сложения неравенства с равенством будет, конечно же, неравенство, чем и объясняется отсутствие противоречия в последней строке. Cтрока подобного типа является признаком несовместности системы уравнений.

является признаком несовместности системы уравнений.

Векторная алгебра

1. Дан треугольник с вершинами в точках A (1,2), B (7,10), C (-1,3).

Найти и определить  он острый или тупой?

Для решения задачи сначала построим символический треугольник с вершинами в точках А, В и С безотносительно к системе координат, поскольку важен только общий принцип вычислений. Угол А=φ при вершине А образован сторонами треугольника АВ и АС или, что то же самое, является углом

между векторами и . Координаты этих векторов находим путем вычитания соответствующих координат конечной и начальной точек: =(6, 8), =(2, 1). Использование формулы скалярного произведения дает

= = = ⇒ cos φ < 0 ⇒ A – тупой в отличие от рисунка.

2. Даны векторы = +2 и = . Найти значения параметра m, при которых ‖ и ⊥ .

Сначала для единообразия запишем первый вектор в координатной форме, т.е. = . Далее, используя пропорциональность координат коллинеарных векторов, находим = 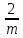. Наконец, раскрывая пропорцию, получаем уравнение =8, откуда m==.

Признаком ортогональности векторов является равенство нулю их скалярного произведения 0==4m+2m=6m, откуда находим m=0. При графической иллюстрации геометрической сути этой задачи рассмотрим возможные расположения векторов в системе координат. На рисунке векторы изображены с совмещенными началами при отрицательных значениях параметра m = 2. Варьирование величиной m влечет одновременное вращение векторов в противоположных направлениях с перемещением концевых точек вдоль соответствующих пунктирных линий. Коллинеарность и ортогональность векторов возникает при вычисленных значениях m.

Аналитическая геометрия

1. Найти уравнение прямой линии l, проходящей через точку =(1, 2) перпендикулярно направлению =(1, 3). В компактной записи – найти l: ∊l  . Поскольку по условию задачи в качестве нормального вектора искомой прямой может быть выбран вектор =, то коэффициентами при переменных в уравнении прямой будут координаты этого вектора

l : .

Используя факт прохождения прямой через заданную точку, найдем С путем подстановки в уравнение ее координат 1+32+С=0, откуда находим С= 5. Тогда

l : .

Направляющим вектором такой прямой будет любой вектор, ортогональный нормальному. Этому условию удовлетворяет вектор = (3, 1).

Упражнение. Найти ее каноническое и параметрические уравнения.

2. Построить прямую : (1, 2) ∊ ∥ . В этом случае вектор может быть принят в качестве направляющего вектора, т.е. =. Такие исходные данные позволяют сразу же построить каноническое уравнение прямой

:

и параметрические уравнения + 3t.

Упражнение. Из канонического получить общее уравнение прямой.

3. Найти уравнение прямой : ∊ ‖.

Требование параллельности прямых означает коллинеарность нормальных векторов и прямых и , вследствие чего можно принять = =(3, 1). Тогда коэффициенты при переменных в искомом уравнении известны : 3x+y+С=0, а для определения свободного члена уравнения достаточно воспользоваться фактом 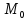∊ , подставив координаты точки в уравнение 31+2+С=0, откуда находим С= 5. В итоге записываем искомое уравнение прямой

: 3x+y5=0.

4. Найти : ∊ 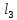⊥. Используя перпендикулярность прямых можно принять =. Таким исходным данным наилучшим образом отвечает каноническое или параметрические уравнения:

.

Упражнение. Построить все остальные уравнения прямой.

5. Найти уравнение прямой, проходящей через точки (1, 1) и (2,3). В качестве направляющего вектора естественно принять

==(3, 2). Тогда по обкатанной схеме получим параметрические уравнения и общее уравнение 2x+3y5=0. Прямой подстановкой нетрудно проверить, что обе заданные точки действительно удовлетворяют общему уравнению, которое тем самым определяет искомую прямую.

6. Геометрическая интерпретация решения системы линейных урав-нений. Ранее в качестве простейших примеров изучались системы с матрицами коэффициентов 2-го порядка. Случай двух переменных помимо простоты привлекателен еще и тем, что позволяет придать решению системы наглядную геометрическую интерпретацию. Теперь мы знаем, что два линейных уравнения системы с двумя переменными задают на плоскости две прямые, которые по своему взаимному расположению могут характеризоваться как пересекающиеся, накладывающиеся друг на друга и параллельные.

В случае пересечения прямых существует единственная общая для них точка – точка пересечения, координаты которой и являются искомыми величинами. Это означает, что решение существует и единственно, т.е. система уравнений – совместная и определенная.

В случае наложения прямых имеется бесконечно большое количество общих точек, что свидетельствует о наличии бесконечного множества решений. Такая система  совместная, но неопределенная.

В случае параллельности прямых общих точек у них нет, что означает отсутствие решения системы, т.е. ее несовместность.

В качестве примера произведем соответствующие геометрические построения для следующих систем.

Прямые, задаваемые этими уравнениями, построены по двум точкам их пересечения с осями координат. Для прямой , полагая одну из переменных равной нулю, имеем: {x  0, y  2}, {x  4, y  0}; для получаем: , . Координаты точки пересечения прямых являются решением системы соответствующей системы линейных уравнений.

Получение единичной матрицы в левой секции расширенной матрицы

обеспечивает единственность решения задачи.

Полученные результаты свидетельствуют об универсальности метода Гаусса в части вычисления решения систем линейных уравнений и выявления случаев неединственности решения или его отсутствия вообще.

Линейное программирование

1. Решить геометрическим способом задачу:

L() = ⟶ min ,

Вершины многогранника допустимых решений найдены как точки пересечения прямых, уравнения которых получены преобразованием неравенств системы условий в равенства. Подсчитаем значения целевой функции в вершинах, координаты которых легко определяются по рисунку как пересечения соответствующих прямых: L()=12, L()=16, L()=64, L()=22. Отсюда следует, что оптимальное решение: = 1.5, = 12.

2. Решить симплекс-методом задачу:

L() = ⟶ mах ,

Введением балансовых переменных и неравенства задачи преобразуются в систему равенств и условий неотрицательности переменных

Выберем в качестве базисных переменных первые три, т.е. выразим их через свободные переменные , , . Стрелки указывают, что сначала выражение из второго уравнения подставляется в первое и третье уравнения, а, затем, с помощью первого уравнения исключается из последнего уравнения и, тем самым, обеспечивается выражение базисных переменных только через свободные.

L= 30 + .

Полагая свободные переменные равными 0, находим начальное допустимое решение =(15, 5, 18, 0, 0, 0), =30.

Первая итерация. Увеличение значения L возможно только за счет роста переменной при =0, =0. Первое и третье равенства допускают неограниченный рост . Однако второе равенство при условии неотрицательности переменной в качестве максимально допустимого значения разрешает лишь =5/2. Тогда следующее допустимое решение

=(20, 0, 28, 2.5, 0, 0), =75/2=37.5 .

Вторая итерация. Теперь в качестве базисных переменных примем

L= 37.5  1.5  0.5.

Поскольку коэффициенты целевой функции при свободных переменных отрицательны, то её дальнейшее увеличение невозможно и решением задачи является предыдущее допустимое решение

= 28, =2.5, =37.5.

3. Решить симплекс-методом задачу:

L() = ⟶ min ,

За счет ввода балансовых переменных , , ограничения задачи преобразуются в систему равенств с равноправными переменными

Выберем переменные , , в качестве базисных и выразим их через свободные переменные и , т.е. приведем систему ограничений задачи к виду

Выразим целевую функцию через свободные переменные

L() = + .

Полагая ==0, найдем =0.5, =1.5, =2.5 и получим начальное допустимое решение =(0, 0.5, 0, 1.5, 2.5), =0.5.

Первая итерация. Уменьшение L возможно только за счет роста . Увеличение этой переменной лимитируют второе и третье равенства. Из условия равенства и нулю, сохраняя =0, находим соответственно =3 и 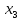=5 и, выбирая наименьшее из них, получаем первое допустимое решение =(0, 2, 3, 0, 1), =2. Теперь в качестве свободных переменных выберем те, которые в базисе имеют нулевые координаты. Второе уравнение позволяет выразить базисную переменную через свободные переменные и . Тогда, подставляя полученное выражение для в остальные уравнения, найдем

L()= 2  + .

Вторая итерация. Уменьшить величину L может только . Два первых уравнения не ограничивают ее рост. Удерживая =0 в третьем равенстве и обеспечивая неотрицательность , найдем максимально допустимое значение =0.2 Подсчитав величины остальных переменных, получим =(0.2, 2.4, 3.6, 0, 0), = 2.2. Взяв свободными переменными и преобразуем два последних уравнения, исключив из них .

L()= 2.2 + 0.8 + 0.2 .

Коэффициенты целевой функции при переменных положительны. Поэтому ее дальнейшее уменьшение невозможно, и тогда решение задачи

= 2.2.

Задачи для самостоятельного решения

1. Найти матрицу С = A + 3B, где A = , B = .

2. Вычислить произведение матриц AB и BA для

А = и В =

3. Найти решение систем линейных уравнений

4. Определить косинус угла между векторами = (1, 2) и = (1, 1) .

5. Дано: =2, =3 и  . Вычислить скалярное произведение

(5 + 3)(2).

6. Решить системы линейных уравнений и сопроводить геометрической интерпретацией:

7. Первую задачу практикума из раздела ЛП решить симплекс-методом.

8. Вторую и третью задачи решить геометрическим способом.

9. Проверить оптимальность решения задачи п.5.7, следуя изложенной

там схеме.

Вопросы для самопроверки

1. Определение матрицы. Классификация матриц по внешнему признаку (прямоугольная, квадратная, вектор-строка, вектор-столбец, число) и внутреннему содержанию (треугольная, диагональная, единичная, нулевая). Операции над матрицами: равенство матриц, сумма матриц, умножение матрицы на число и на другую матрицу. Примеры практического применения матричной алгебры.

2. Определение системы линейных уравнений и ее решения. Совместность, неопределенность, несовместность. Расширенная матрица. Метод Гаусса. Элементарные преобразования. Балансовая модель Леонтьева.

3. Понятие вектора, модуль вектора. Равенство векторов. Сложение векторов, умножение вектора на число, скалярное произведение векторов. Геометрия операций над векторами. Аналитические признаки коллинеарности и ортогональности векторов. Базис, декартова система координат. Реализация операций над векторами в координатах.

4. Аналитический и геометрический способы задания линии, их эквивалентность. Точка и направляющий вектор как идентификаторы прямой. Уравнения прямой линии (векторное, параметрические, каноническое, общее). Задачи о прямых: выявление особенностей прямой по ее уравнению; построение уравнения прямой, проходящей через заданную точку параллельно и перпендикулярно заданному направлению (прямой линии); нахождение уравнения прямой, проходящей через две заданные точки; вычисление точки пересечения двух прямых; выявление параллельности и наложения прямых; геометрическая интерпретация решения системы двух уравнений с двумя неизвестными.

5. Формулировка оптимизационной задачи, ее формализация в рамках линейного программирования и частные постановки (общая, дробно-линейная, транспортная). Целевая функция задачи линейного программирования, критерий оптимальности, система ограничений. Многогранник допустимых решений, оптимальное решение. Геометрический способ решения задачи ЛП. Алгоритмическая основа симплекс-метода. Разновидности математического программирования (целочисленное, нелинейное, динамическое).

Контрольные

Контрольная 1

1. Вычислить  3 .

2. Перемножить матрицы .

3. = (1, –1), = (0, 1), + = ? = ? Проверить ‖ , ⊥ .

4. Решить СЛУ и дать геометрическую интерпретацию

5. Построить уравнения прямых и :

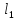= (1, 1) ∊ ⊥ = (1, –3); ∊ ‖ .

Контрольная 2 (внеаудиторная)

Задачи ЛП решить геометрически и симплекс-методом:

L() = ⟶ min, L() = ⟶ max ,

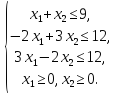
Ч А С Т Ь 2

Т Е О Р И Я В Е Р О Я Т Н О С Т Е Й