1. Матрицы

1.1.Понятие матрицы

Таблица чисел (символов) из m строк и n столбцов называется прямоугольной матрицей размерности m×n, а составляющие ее элементы – элементами матрицы. В дальнейшем будут рассматриваться только числовые матрицы.

Традиционно принята следующая система символьных обозначений:

матрица – прописная латинская буква, а ее элемент – одноименная строчная буква с указанием двух индексов, означающих номера строки и столбца, в которых находится конкретный элемент. Матрицы классифицируются по внешнему признаку и внутреннему содержанию.

Сначала разберемся с внешним признаком, под которым подразумевается конфигурация матрицы как геометрической фигуры. Запись

А==

описывает прямоугольную матрицу A размерности m×n, у которой на пересечении i-й строки и j-го столбца находится элемент .

Если m=1, то матрица состоит из одной единственной строки = и потому называется вектор-строка.

Если же n=1, то имеем вектор-столбец

.

Если m=n=1, то матрица содержит одно единственное число Таким образом, число является частным случаем более общей структуры, каковой является матрица.

Особый случай представляют собой квадратные матрицы, у которых

m=n. При этом говорят уже не о размерности, а о порядке матрицы n.

В структуре квадратной матрицы линия из левого верхнего угла в нижний правый называется главной диагональю. Элементы с одинаковыми индексами, находящиеся на этой линии, называются элементами главной диагонали.

Среди квадратных матриц в соответствии с их содержимым выделяются следующие виды, перечисленные ниже.

Матрица, у которой либо под, либо над главной диагональю находятся только нули, называется треугольной. В приведенных ниже примерах треугольных матриц 3-го порядка символом "⋆" обозначены не нулевые элементы

, , , , .

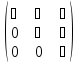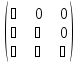Матрица с хотя бы частично отличной от нуля одной только главной диагональю называется диагональной

, . .

Если же диагональ заполнена одними единицами, то такая матрица называется единичной. Для нее принято специальное обозначение

Е=

Матрица, состоящая из одних нулей, называется нулевой и обозначается

== .

1.2. Арифметические операции над матрицами

На множестве матриц сначала определяется понятие равенства как важнейшего элемента любой математической операции, после чего вводятся арифметические операции. Умея сравнивать только два числа от равных матриц логично потребовать равенства их соответствующих элементов, т.е. находящихся в матрицах на одних и тех же местах, что автоматически влечет требование одинаковой размерности матриц. В соответствии с этим под равенством матриц понимается равенство их размерностей и всех соответствующих элементов, что с помощью введенной ранее символики может быть записано следующим образом:

Над матрицами, как и над числами, можно производить арифмети- ческие операции сложения и умножения на число. Поскольку реально складывать мы умеем только два числа, то сложение двух совокупностей чисел, оформленных в виде матриц, разумно свести к этой парной операции, применяемой к соответствующим элементам матриц.

Сложение (вычитание) двух матриц осуществляется путем суммирования их соответствующих элементов и определяется для матриц одинаковой размерности по соображениям аналогичным равенству:

Умножение матрицы на число сводится к умножению на это число каждого элемента матрицы:

Таким образом, операции сложения матриц и умножения на число распространяются на их элементы.

Эти операции приводят к матрице с противоположным знаком

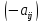(–1)А= = –А

и нулевой матрице

0=

При этом нулевая матрица как и числовой 0 не меняет второе слагаемое

A+ =A, А+(–A)=А–A=.

Из правил выполнения арифметических операций над матрицами вытекают их алгебраические свойства.

1. Сложение матриц коммутативно А+В=В+А.

2. Сложение матриц ассоциативно А+(В+С)=(А+В)+С.

3. Умножение матрицы на число ассоциативно λ(μA)= (λμ)A.

4. Умножение матрицы на число дистрибутивно относительно сложе-

ния чисел (λ+μ)A=λA+μA и матриц λ(A+B)=λA+μB.

Эти равенства слева направо читаются так  скобки можно рас-

крывать, а в обратном порядке  общий множитель, как число,

так и матрицу можно выносить за скобки.

5. Матрица не меняется, если ее сложить с нулевой матрицей

А+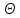 = +А=А, откуда А–А=,

т.е. 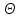на множестве матриц играет роль, аналогичную нулю на множестве действительных чисел.

Пример суммы двух матриц с умножением второй матрицы на число:

 = + = = .

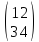
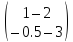После сложения матриц и умножения матрицы на число следующим шагом является определение способа умножения двух матриц. Однако сделать это на основе каких-либо простых соображений на сей раз уже не представляется возможным. Словесное содержание алгоритма умножения матриц звучит следующим образом. Для того чтобы умножить одну матрицу на другую, надо все строки первой матрицы последовательно умножить на все столбцы второй матрицы. Умножение -й строки на 𝑗-й столбец осуществляется путем попарного перемножения их соответствующих элементов и сложения полученных результатов. При этом будет получен элемент результирующей матрицы -й строки и 𝑗-го столбца. Данное правило требует наличия соответствующих элементов в строке и столбце, а это означает, что длина строки (количество столбцов) первой матрицы должна быть равна длине столбца (количеству строк) второй матрицы.

Аналитически это правило записывается в следующем виде

=

Таким образом, элемент результирующей матрицы вычисляется в виде суммы попарных произведений соответствующих элементов строки и столбца. Схематически умножение матриц можно представить так, как это сделано ниже в окаймлении рамки.

=

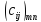
j

Пример:

Если же сомножители поменять местами, то получится совершенно другой результат  матрица иная не только по содержимому, но и вообще другой размерности:

Эти примеры показывают, что результат умножения двух матриц зависит от того, в какой последовательности матрицы взяты как сомножители. Такое свойство называется некоммутативностью.

Ниже сформулированы основные свойства произведения матриц.

1. Некоммутативность АВ≠ВА.

2. λ

3. Ассоциативность A(BC)=(AB)С.

4. Дистрибутивность относительно сложения матриц

(А+В)С=АС+ВС,

т.е., с одной стороны можно раскрывать скобки, а с другой –

матрицу как общий множитель можно выносить за скобки.

По причине некоммутативности произведения матриц используется следующий термин: умножить матрицу А на В справа АВ или слева ВА. Таким образом, указывается та сторона матрицы А, где матрица В находится как сомножитель.

Очевидное свойство матрицы Е заключается в том, что при умножении она не меняет второй сомножитель AE=EA=A и произведение в данном случае коммутативно. Именно за это качество матрица E и названа единичной, поскольку на множестве матриц она играет роль единицы. В качестве упражнения стоит проверить, что матрица, состоящая исключительно из одних единиц, этому условию не удовлетворяет.