Контрольные задания
Задание 1. Найдите седловую точку следующей платежной матрицы:
.
Задание 2. На основе следующей платежной матрицы определите седловую точку:
.
Задание 3. Найдите седловую точку для платежной матрицы:
.
Задание 4. Найдите седловую точку следующей платежной матрицы:
.
Задание 5. Определите максиминную и минимаксную стратегии для платежной матрицы:
.
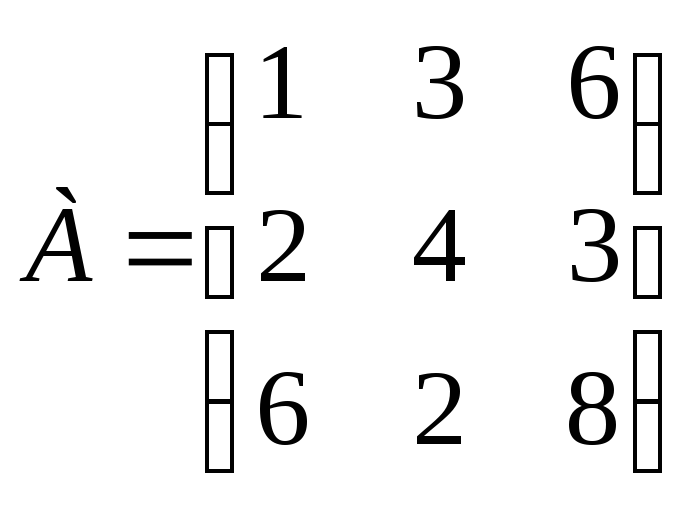Задание 6. Решите аналитически, используя понятие доминирования, игру, определяемую следующей платежной матрицей:
.
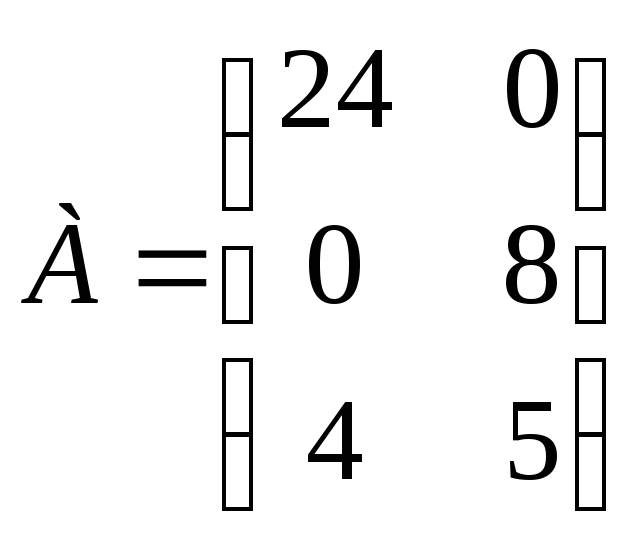Задание 7. Уменьшите размеры следующей платежной матрицей, используя понятие доминирования:
.
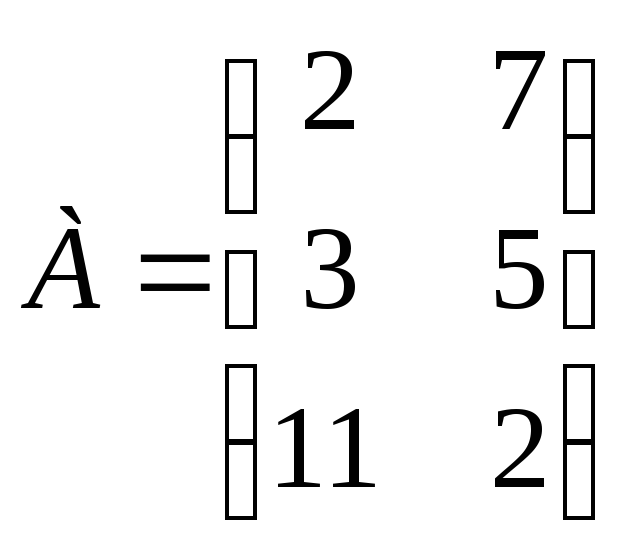Задание 8. Решите аналитически, используя понятие доминирования, игру, определяемую следующей платежной матрицей:
.
Задание 9. Определите нижнюю и верхнюю цены игры, заданной матрицей выигрышей:
.
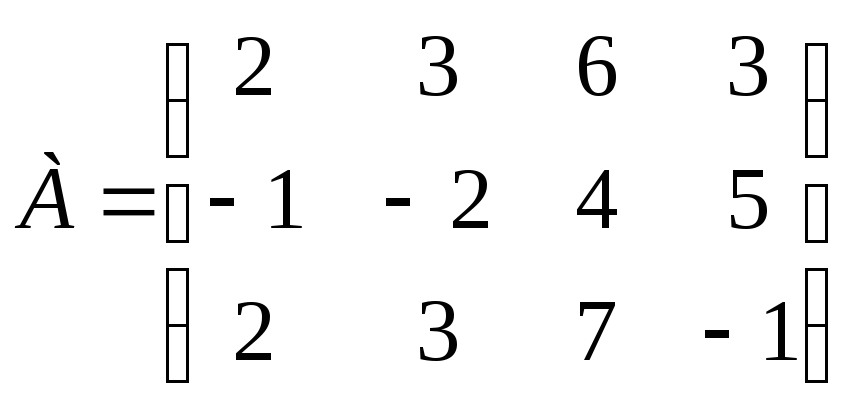Задание 10. Перейдите от матрицы выигрышей к матрице рисков:
.
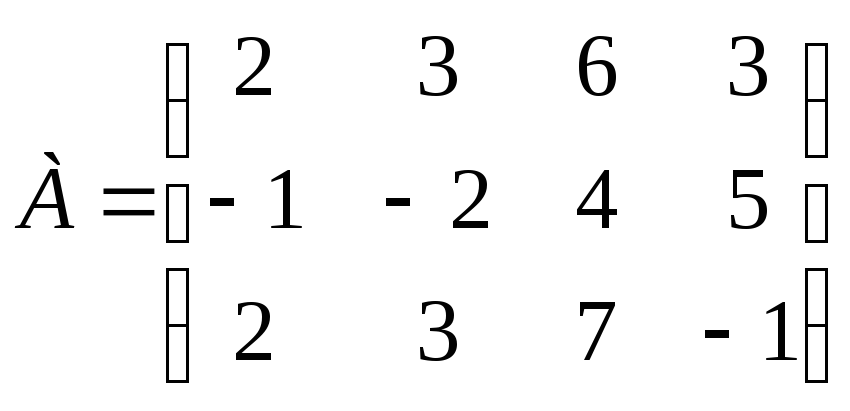Задание 11. Используя понятие доминирования, уменьшите размеры следующей платежной матрицы:
.
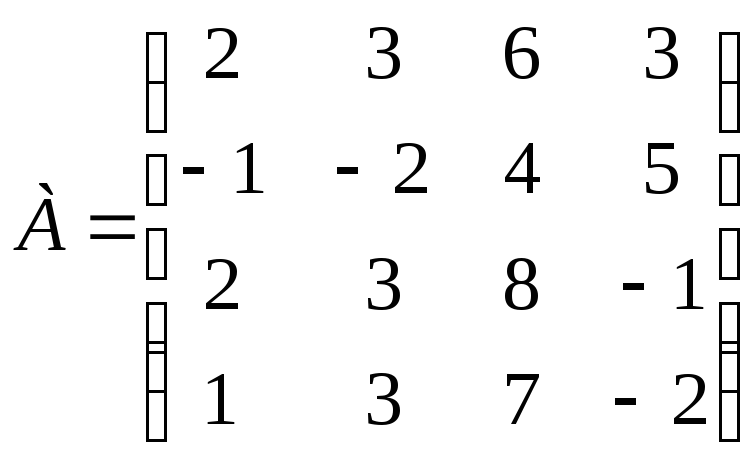Задание 12. Игра с природой задана матрицей выигрышей:
.
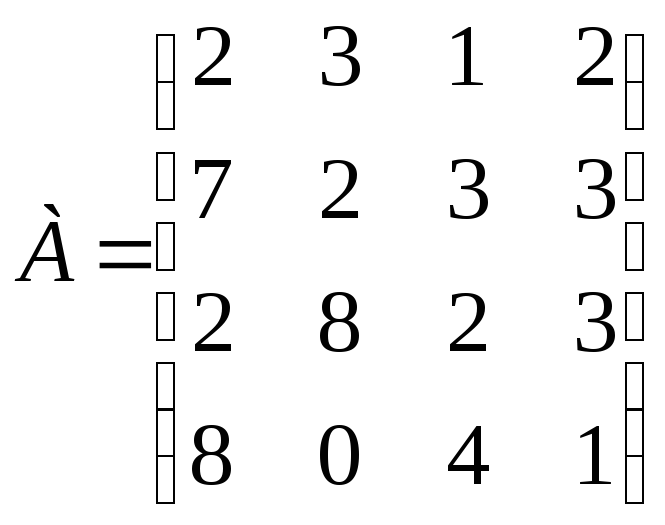Найдите оптимальную стратегию игрока 1, используя в качестве априорной информации о поведении природы критерии Вальда, Сэвиджа и Гурвица (р = 0,6).
Задание 13. Платежная матрица имеет вид:
.
Найдите максиминную и минимаксную стратегии для заданной платежной матрицы. Укажите, имеет ли данная матрица игры седловую точку.
Задание 14. Определите, имеет ли заданная платежная матрица седловую точку.
.
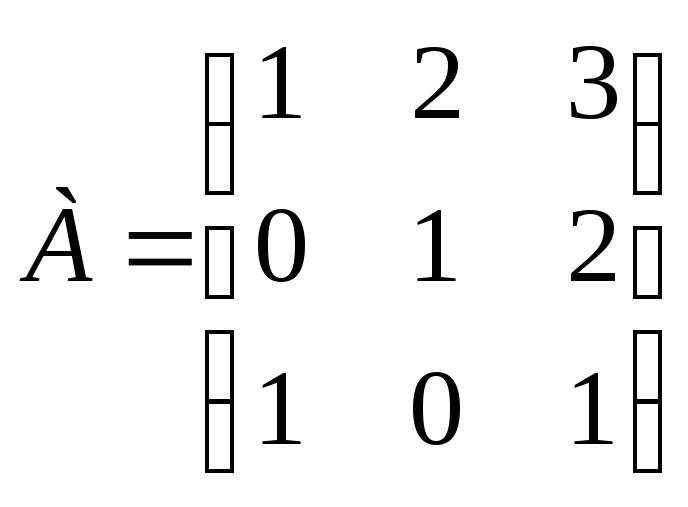Задание 15. Найдите наилучшие стратегии по критериям: максимакса, Вальда, Сэвиджа, Гурвица (применительно к матрице выигрышей коэффициент пессимизма-оптимизма равен 0,2; применительно к матрице рисков коэффициент пессимизма-оптимизма равен 0,4) для следующей платежной матрицы игры с природой:
.
Задание 16. Дана матрица игры с природой в условиях полной неопределенности:
.
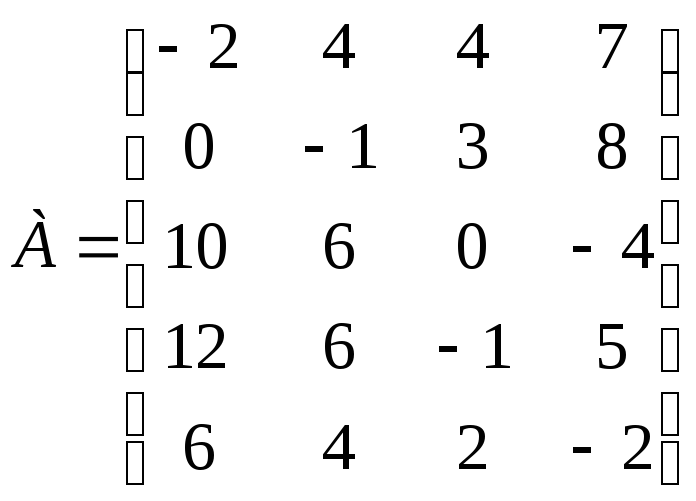Проанализируйте оптимальные стратегии игрока 1, используя критерии пессимизма- оптимизма Гурвица применительно к платежной матрице А и матрице рисков R р = 0; 0,5; 1; при этом выделите критерии максимакса, Вальда и Сэвиджа; установите, какую роль играют стратегии ЛПР при р = 0,5.
Задание 17. Анализируется матрица выпуска новых видов продукции, приведенная в таблице. Определите оптимальную стратегию с помощью критерия Вальда.
Эффективность выпуска новых видов продукции
|
Варианты решений |
Варианты условий обстановки |
||
|
П1 |
П2 |
П3 |
|
|
А1 |
0,25 |
0,35 |
0,40 |
|
А2 |
0,75 |
0,20 |
0,30 |
|
А3 |
0,35 |
0,82 |
0,10 |
|
А4 |
0,80 |
0,20 |
0,35 |
Задание 18. Анализируется матрица потерь при выпуске новых видов продукции. Определите наиболее выгодную стратегию с помощью критерия Сэвиджа.
Величина потерь при выпуске новых видов продукции
|
Виды решений |
Варианты обстановки |
||
|
П1 |
П2 |
П3 |
|
|
А1 |
0,55 |
0,47 |
0,00 |
|
А2 |
0,05 |
0,62 |
0,10 |
|
А3 |
0,45 |
0,00 |
0,30 |
|
А4 |
0,00 |
0,72 |
0,05 |
Задание 19. На основе матрицы выигрышей определите наиболее выгодную стратегию с помощью критерия Вальда.
.
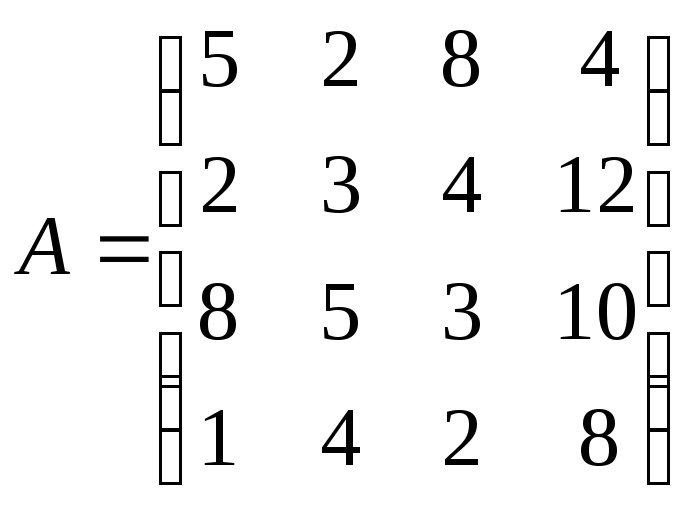Задание 20. На основе матрицы рисков определите наиболее выгодную стратегию с помощью критерия Сэвиджа.
.
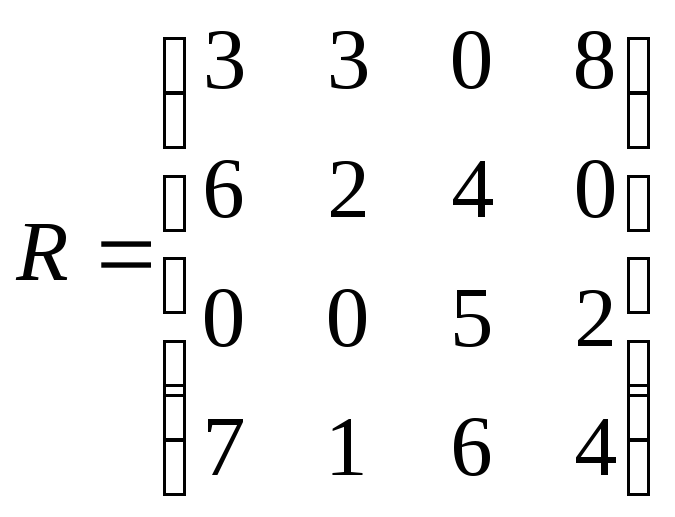Задание 21.
Анализируется матрица полезного
результата. При значении коэффициента
пессимизма-оптимизма р
=
,
найдите оптимальную стратегию с помощью
критерия Гурвица.
.
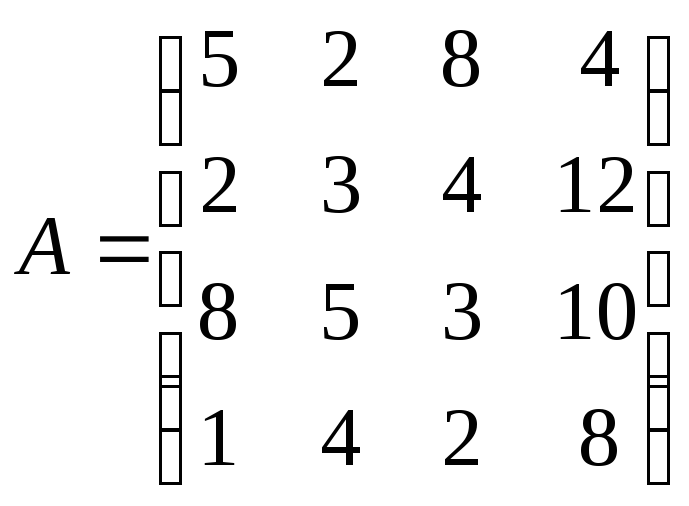Задание 22.
Анализируется матрица коммерческого
риска. При значении коэффициента
пессимизма-оптимизма р
=
,
найдите оптимальную стратегию с помощью
критерия Гурвица.
.
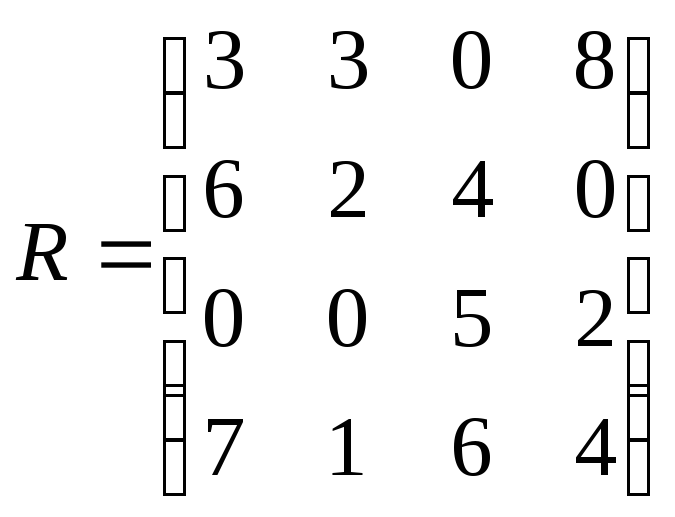Задание 23. На основе матрицы выигрышей определите наиболее выгодную стратегию с помощью критерия максимакса.
.
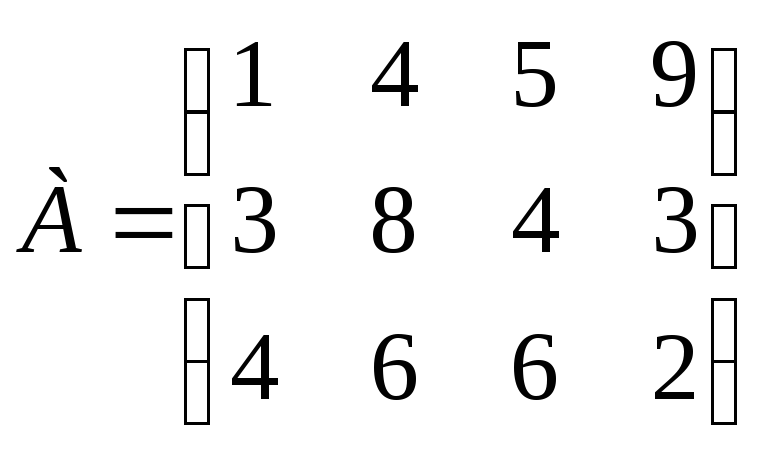Задание 24. На основе матрицы выигрышей определите наиболее выгодную стратегию с помощью критерия Вальда.
.
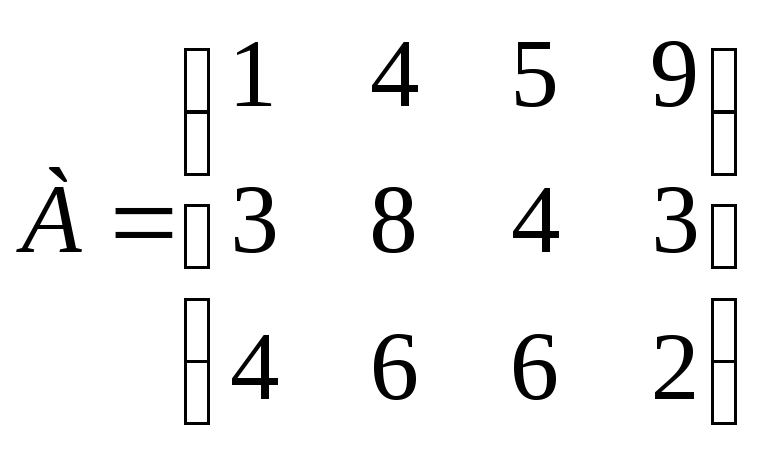Задание 25. С помощью критерия Сэвиджа определите наиболее выгодную стратегию на основе матрицы рисков.
.
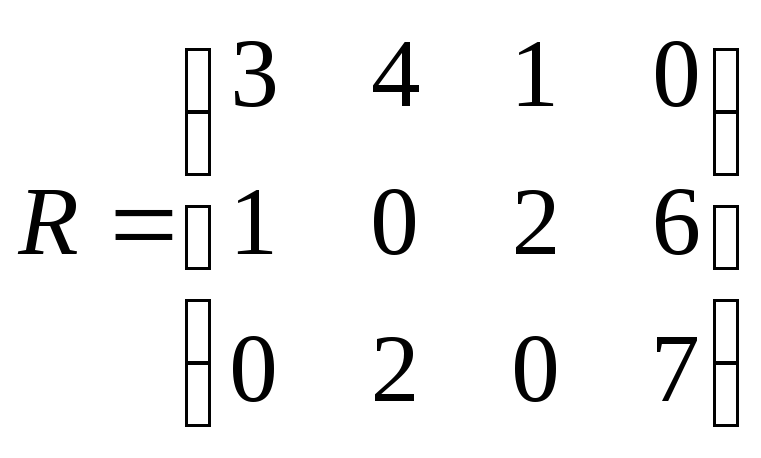Задание 26. Анализируется матрица выигрышей. При значении коэффициента пессимизма-оптимизма р = 0,5 найдите оптимальную стратегию с помощью критерия Гурвица.
.
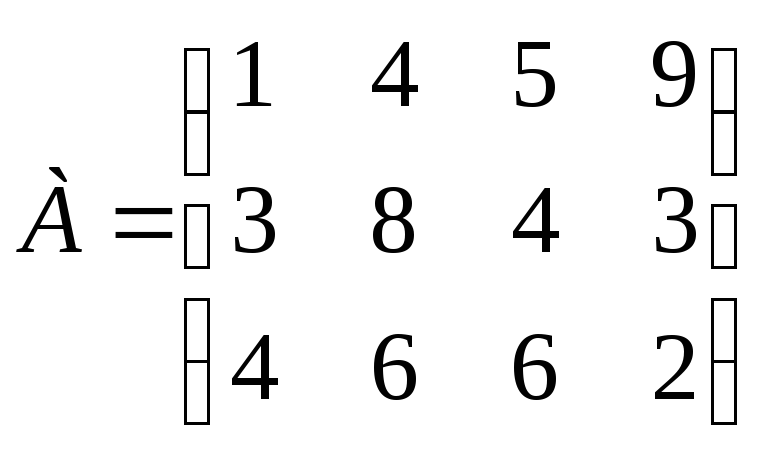Задание 27. Анализируется матрица рисков. При значении коэффициента пессимизма-оптимизма р = 0,5 найдите оптимальную стратегию с помощью критерия Гурвица.
.
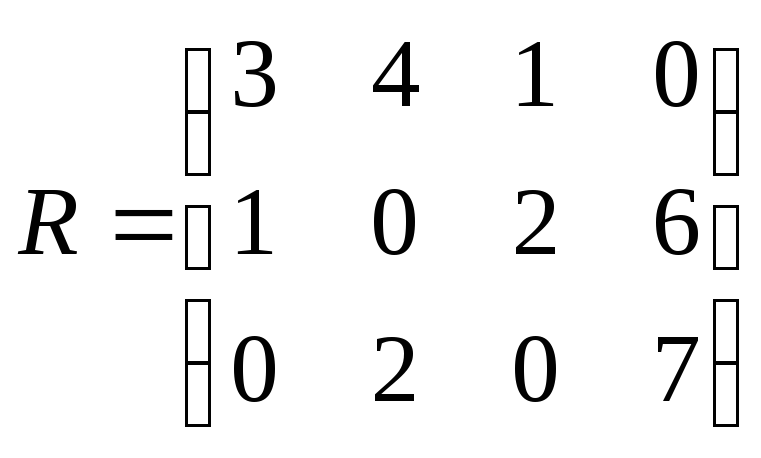Задание 28. Используя понятие доминирования, уменьшите размеры следующей платежной матрицы:
.
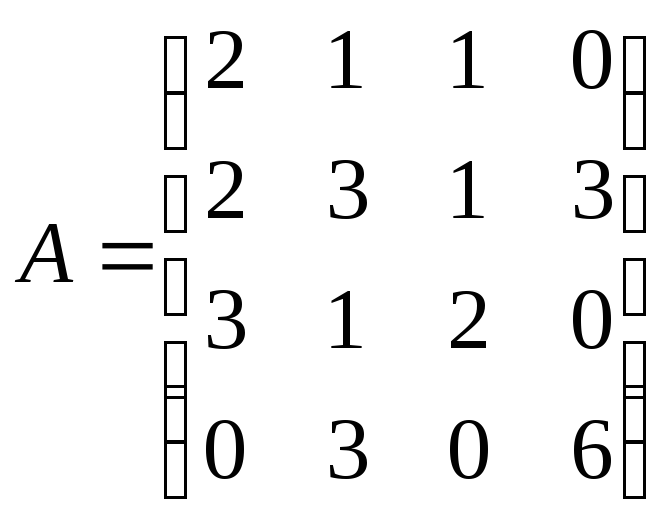Задание 29. Найдите максиминную и минимаксную стратегии для платежной матрицы:
.
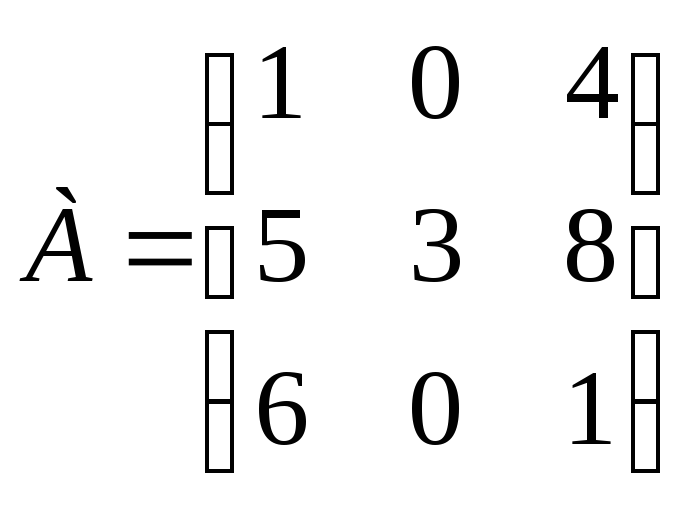Задание 30. Уменьшите размеры следующей платежной матрицей, используя понятие доминирования:
.
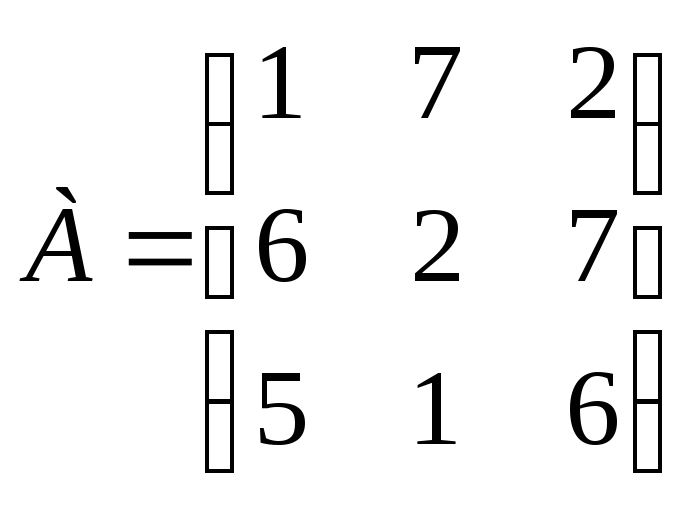Задание 31. Определите максиминную и минимаксную стратегии при заданной матрице эффективности:
.
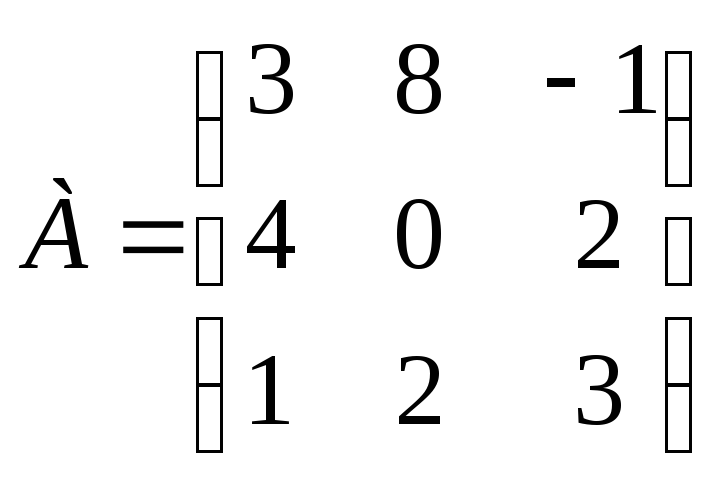Задание 32. Определите верхнюю и нижнюю цены при заданной матрице игры и укажите максиминную и минимаксную стратегии:
.
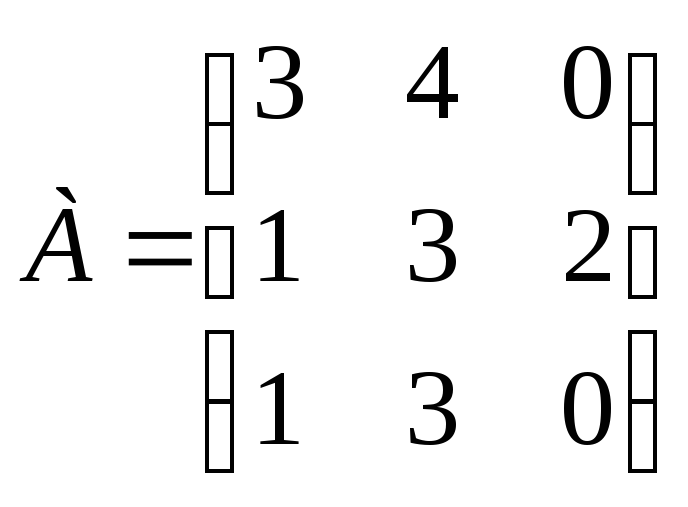Задание 33. Найдите максиминную и минимаксную стратегии для платежной матрицы:
.
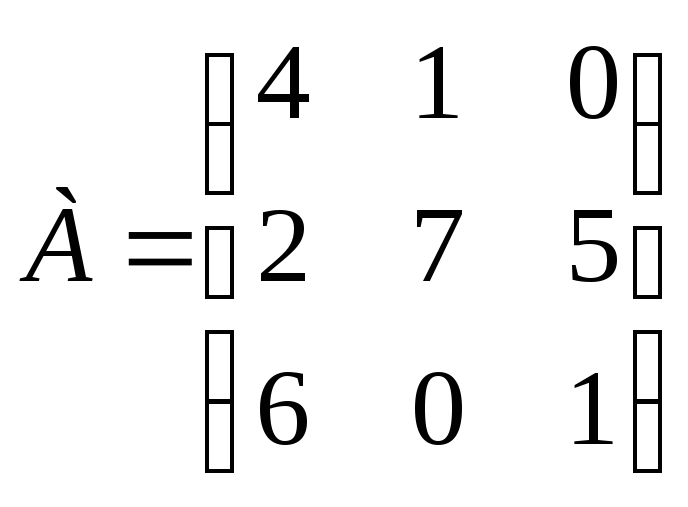Задание 34. Платежная матрица имеет вид:
.
Определите верхнюю и нижнюю цены для заданной платежной матрицы и укажите максиминную и минимаксную стратегии.