
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
16.2.3. Інтеграл Коші. Інтегральна формула Коші
Теорема
2.2. Нехай
функція f(z) аналітична в замкненій
однозв'язній області
 і
L – межа області D. Тоді має місце формула
і
L – межа області D. Тоді має місце формула
 ,
(2.5)
,
(2.5)
де
 - будь-яка точка всередині області D, а
інтегрування по контуру L проводиться
в додатному напрямку (тобто проти
годинникової стрілки).
- будь-яка точка всередині області D, а
інтегрування по контуру L проводиться
в додатному напрямку (тобто проти
годинникової стрілки).
Інтеграл, що знаходиться в правій частині рівності (2.5), називається інтегралом Коші, а сама ця формула називається інтегральною формулою Коші.
Формула Коші (2.5) є однією з найважливіших у теорії функцій комплексної змінної. Вона дозволяє знаходити значення аналітичної функції f(z) в будь-якій точці z0, що лежить всередині області D через її значення на межі цієї області.
Побудуємо
коло lr
з центром у будь-якій точці
z0
, взявши радіус r
настільки малим, щоб дане коло було
повністю розташоване всередині області
(щоб lr
не перетинало
L).
Отримаємо
двозв’язну
область D1
(заштриховану на рис. 12), обмежену
контурами
L
і
lr,
в якій функція
 аналітична.
аналітична.
Тоді, відповідно до наслідку 1 з теореми Коші, маємо:
Рис.
12
 .
.
Звідси випливає:

 .
.
Але
 (див. приклад 8), тому
(див. приклад 8), тому
 ,
,
тобто
 . (2.6)
. (2.6)
Оцінимо
різницю в лівій частині рівності (2.6).
Оскільки аналітична функція f(z)
неперервна в точці
 ,
то для будь-якого числа
,
то для будь-якого числа
 знайдеться число
знайдеться число
 таке, що при
таке, що при
 (на колі lr
маємо
(на колі lr
маємо
 )
виконується нерівність
)
виконується нерівність
 .
.
Застосовуючи властивість 6 про оцінку модуля інтеграла (п. 2.1), маємо:
 .
.
Число
 може бути вибране як завгодно малим, а
ліва частина останньої нерівності не
залежить від
може бути вибране як завгодно малим, а
ліва частина останньої нерівності не
залежить від
 ,
то вона дорівнює нулю:
,
то вона дорівнює нулю:
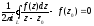 ,
,
звідси випливає формула (2.5).
Відзначимо, що інтегральна формула Коші (2.5) виконується для багатозв’язної області: кожний з контурів обходиться так, щоб область D залишалася ліворуч.
Застосовуючи інтегральну формулу Коші, можна довести наступні теореми-наслідки.
Теорема
2.3. Для
всякої диференційовної у точці z функції f(z) існують похідні всіх порядків,
причому n-а похідна має вигляд:
функції f(z) існують похідні всіх порядків,
причому n-а похідна має вигляд:
 .
(2.7)
.
(2.7)
Таким чином, похідна аналітичної функції також є аналітичною функцією.
Нагадаємо,
що з диференційовності дійсної функції
не випливає навіть існування другої
похідної (функція
 має похідну в точці x=0,
а похідна цієї функції
має похідну в точці x=0,
а похідна цієї функції
 при
x=0
не існує).
при
x=0
не існує).
Теорема
2.4. В
околі кожної точки z ,
де існує похідна f(z),
функція f(z)
,
де існує похідна f(z),
функція f(z)
може бути подана збіжним рядом:
 (2.8)
(2.8)
Ряд (2.8) називається рядом Тейлора функції f(z) у точці z0.
Ряд Тейлора диференційовної в точці z0 функції існує та збігається до самої функції. Ряд же Тейлора для дійсної функції f(z) може збігатися до іншої функції або бути розбіжним.
Зауваження. Формула n-ї похідної функції f(z) може бути отримана з формули Коші
 (2.9)
(2.9)
(у формулі
(2.5) замінимо z
на
 ,
z0
на
z)
шляхом послідовного диференціювання
рівності (2.9) по z:
,
z0
на
z)
шляхом послідовного диференціювання
рівності (2.9) по z:
 . (2.10)
. (2.10)
Формули (2.5) і (2.7) можна використовувати для обчислення інтегралів по замкнених контурах.
Приклад
9.
Обчислити
 ,
де а) L
-
коло
|z|=1,
б)
L
- коло
|z-i|=2.
,
де а) L
-
коло
|z|=1,
б)
L
- коло
|z-i|=2.
○ а)
функція
 є аналітичною в області
є аналітичною в області
 .
За теоремою Коші маємо
.
За теоремою Коші маємо
 .
.
б)На рисунку 13 зображена область,
Рис. 13 обмежена контуром інтегрування.
В цій
області
 знаходиться точка
знаходиться точка
 ,
в якій знаменник підінтегральної функції
дорівнює нулю. Перепишемо інтеграл у
вигляді
,
в якій знаменник підінтегральної функції
дорівнює нулю. Перепишемо інтеграл у
вигляді
 .
.
Функція
 є аналітичною в даній області. Застосовуючи
інтегральну формулу Коші (2.5), знаходимо:
є аналітичною в даній області. Застосовуючи
інтегральну формулу Коші (2.5), знаходимо:
 . ●
. ●
Приклад
10.
Обчислити
 .
.
○ Всередині
кола і на його межі |z|=1
функція
 аналітична. Тому, внаслідок формули
(2.7), маємо
аналітична. Тому, внаслідок формули
(2.7), маємо
 . ●
. ●
