
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
16.1.3. Основні елементарні функції комплексної змінної
Визначимо
основні елементарні функції комплексної
змінної
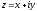 .
.
16.1.3.1. Показникова функція
Показникова
функція
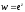 визначається формулою:
визначається формулою:
 (1.1)
(1.1)
Поклавши
в цій рівності
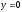 .
Встановлюємо, що для дійсних значень
.
Встановлюємо, що для дійсних значень
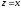 показникова функція
показникова функція
 збігається з показниковою функцією
дійсної змінної:
збігається з показниковою функцією
дійсної змінної:
 .
.
Показникова
функція
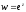 володіє «відомою» властивістю:
володіє «відомою» властивістю:
 .
Дійсно, за правилом множення комплексних
чисел («модулі перемножуються, а аргументи
додаються»), отримуємо:
.
Дійсно, за правилом множення комплексних
чисел («модулі перемножуються, а аргументи
додаються»), отримуємо:
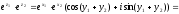
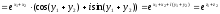 .
.
Аналогічно
можна переконатися в справедливості
властивостей:
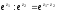 ,
,
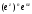
 .
.
Враховуючи,
що
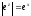 ,
а
,
а
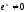 ,
стверджуємо, что показникова функція
,
стверджуємо, что показникова функція
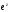 ніде в нуль не обертається, тобто
ніде в нуль не обертається, тобто
 .
.
Виходячи з означення, легко переконатися, що
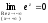 ,
, 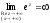 ,
,
вираз
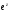 при
при
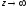 не має змісту.
не має змісту.
Поклавши
в рівності (1.1)
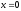 ,
,
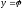 ,
одержимо класичну формулу Ейлера
,
одержимо класичну формулу Ейлера
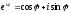 .
За її допомогою, зокрема, можна подати
тригонометричну форму комплексного
числа
.
За її допомогою, зокрема, можна подати
тригонометричну форму комплексного
числа
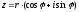 в більш компактній формі
в більш компактній формі
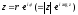 ,
що називається показниковою
формою комплексного
числа .
,
що називається показниковою
формою комплексного
числа .
Показникова
функція комплексної змінної володіє і
специфічною властивістю: вона є
періодичною
з уявним основним періодом
 .
.
Дійсно,
 ,
,
тобто
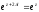 .
Відзначимо, що
.
Відзначимо, що
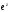 може бути довільним числом крім
може бути довільним числом крім
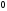 .
Оскільки комплексні числа не порівнюються
то не будемо порівнювати
.
Оскільки комплексні числа не порівнюються
то не будемо порівнювати
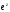 з числом
з числом
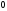 ,
як це робилося у дійсному аналізі :
,
як це робилося у дійсному аналізі :
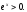
16.1.3.2. Логарифмічна функція
Ця
функція означається як функція, обернена
до показникової: число
 називається логарифмом
числа
називається логарифмом
числа
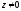 ,
якщо
,
якщо
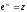 ,
позначається
,
позначається
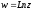 .
Оскільки значення показової функції
.
Оскільки значення показової функції
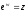 завжди відмінні від нуля, то логарифмічна
функція
завжди відмінні від нуля, то логарифмічна
функція
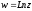 визначена на всій площині
визначена на всій площині
 ,
крім точки
,
крім точки
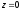 (а отже, має сенс і вираз
(а отже, має сенс і вираз
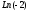 ).
).
Поклавши
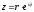 ,
,
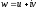 ,
одержимо, відповідно до означення
логарифмічної функції,
,
одержимо, відповідно до означення
логарифмічної функції,
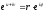 ,
або
,
або
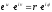 .
Звідси маємо:
.
Звідси маємо:
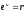 ,
,
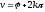 ,
тобто
,
тобто
 ,
,
 (
(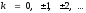 ).
).
Отже,
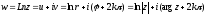 ,
(1.2)
,
(1.2)
тобто
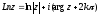 чи,
чи,
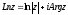 ,
де
,
де
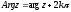 .
.
Формула
(1.2) показує, что логарифмічна функція
комплексної змінної має нескінченну
множину значень, тобто
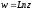 – багатозначна функція.
– багатозначна функція.
Однозначну
вітку цієї функції можна виділити,
підставивши у формулу (1.2)
певне значення
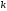 .
Поклавши
.
Поклавши
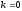 ,
одержимо однозначну функцію, що
називається головним
значенням логарифма
,
одержимо однозначну функцію, що
називається головним
значенням логарифма
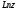 і позначаються символом
і позначаються символом
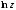 :
:
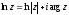 ,
де
,
де
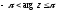 .
(1.3)
.
(1.3)
Якщо
 - дійсне додатне число, то
- дійсне додатне число, то
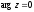 і
і
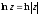 ,
тобто головне значення логарифма
додатнього числа збігається із звичайним
натуральним логарифмом цього числа.
,
тобто головне значення логарифма
додатнього числа збігається із звичайним
натуральним логарифмом цього числа.
Формулу
(1.2) можна переписати так:
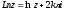 .
.
З формули
(1.2) випливає, что логарифмічна функція
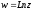 має відомі властивості логарифма дійсної
змінної:
має відомі властивості логарифма дійсної
змінної:
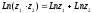 ,
,
 ,
,
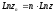 ,
,
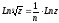 .
.
Доведемо, наприклад, першу властивість:
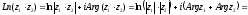
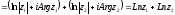 .
.
Приклад
2.
Обчислити
 ;
;
 ;
;
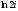 .
.
○Для
числа
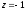 маємо
маємо
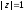 ,
,
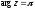 .
Отже,
.
Отже,
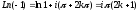 ,
,
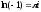 (формули (1.2)
і (1.3));
(формули (1.2)
і (1.3));
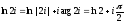 .
●
.
●
16.1.3.4. Степенева функція w=zn
Якщо
 – натуральне
число, то степенева функція визначається
рівністю
– натуральне
число, то степенева функція визначається
рівністю
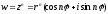 .
Функція
.
Функція
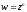 - однозначна.
- однозначна.
Якщо
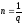
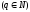 ,
то в цьому випадку
,
то в цьому випадку
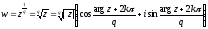 ,
,
де
 .
.
Тут
функція
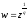 є багатозначна (
є багатозначна (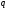 -значна) функція. Однозначну вітку цієї
функції можна одержати, поклавши
-значна) функція. Однозначну вітку цієї
функції можна одержати, поклавши
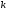 певне значення, наприклад
певне значення, наприклад
 .
.
Якщо
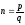 ,
де
,
де
 ,
то степенева функція визначається
рівністю
,
то степенева функція визначається
рівністю
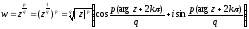 .
.
Функція
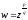 - багатозначна.
- багатозначна.
Степенева
функція
 з довільним комплексним показником
з довільним комплексним показником
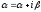 визначається рівністю
визначається рівністю
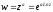 .
.
Функція
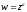 визначена для усіх
визначена для усіх
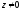 ,
є багатозначною функцією. Так,
,
є багатозначною функцією. Так,
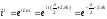 ,
де
,
де
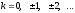
При
 маємо:
маємо:
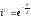 .
.
