16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції

Як уже знаємо, особливою точкою функції f(z) називається точка, у якій функція не є аналітичною.

Особлива точка z=z₀ функції f(z) називається ізольованою, якщо в деякому її околі функція f(z) не має інших особливих точок.

Якщо z₀ — ізольована особлива точка функції f(z), то існує таке число R>0, що в кільці функція f(z) буде аналітичною а, отже, розкладається в ряд Лорана (3.11):

При цьому можливі випадки:

1. Ряд Лорана не містить головної частини, тобто в ряді немає членів з від’ємними показниками. У цьому випадку точка z₀ називається усувною особливою точкою функції f(z).

2. Розклад Лорана містить у своїй головній частині скінчену кількість членів, тобто в ряді скінчена кількість членів з від’ємними показниками. У цьому випадку точка z₀ називається полюсом функції f(z).

3. Розклад Лорана містить у своїй головній частині нескінченну кількість членів, тобто в ряді нескінченно багато членів з від’ємними показниками. У цьому випадку точка z₀ називається істотно особливою точкою функції f(z).

Розглянемо особливості поведінки аналітичної функції f(z) в околі особливої точки кожного типу.

Усувні особливі точки

Якщо z₀ — усувна особлива точка, то в околі точки z₀ розклад (3.11) має вигляд . Цей розклад справедливий у всіх точках круга , крім точки z = z₀. Якщо покласти f(z₀)=c₀ , де (тобто визначити функцію f(z) у точці z₀), то функція f(z) стане аналітичною у всіх точках круга (включаючи його центр z = z₀); особливість точки z₀ усувається, точка z₀ стає правильною точкою функції f(z)).

З рівності 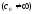слідує, що в досить малому околі усувної особливої точки функція f(z) є обмежена.

Справедливе і обернене твердження: ізольована особлива точка z=z₀ є усувною, якщо існує скінчена границя .

Полюси

Якщо z₀ — полюс, то в околі точки z₀ розклад (3.11) має вигляд де В цьому випадку полюс z₀ називається полюсом m-го порядку функції f(z); якщо m=1, то полюс z₀ називається простим.

Запишемо останню рівність у вигляді

або

(3.16)

де g(z) — аналітична функція, причому Звідси випливає, що f(z) при ­zz₀, тобто в досить малому околі полюса функція f(z) нескінченно велика.

Справедливе і обернене твердження: ізольована особлива точка z=z₀ є полюсом, якщо .

З рівності (3.16) маємо . Звідси отримуємо зручний спосіб обчислення порядку полюса z₀: якщо

(3.17)

то точка z₀ є полюс m-го порядку.

Існує зв'язок між нулем і полюсом функції.

Теорема 3.5. Якщо точка z₀ — нуль m-го порядку функції f(z), то z₀ є полюсом m-го порядку функції ; якщо точка z₀ — полюс m-го порядку функції f(z), то z₀ є нулем m-го порядку функції .

□

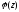Доведемо першу частину теореми. Нехай z=z₀ є нуль m-го порядку для функції f(z). Тоді має рівність , де аналітична в точці z₀ , причому . Тоді і . Це означає (див. (3.17)), що для функції точка z=z₀ є полюсом m-го порядку. Друга частина теореми (оберненої) доводиться аналогічно. ■