
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
-
Ряд Лорана
Теорема
3.4.
Всяка
аналітична в кільці
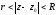
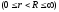 функція
функція
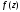 може бути розкладена в цьому кільці в
ряд
може бути розкладена в цьому кільці в
ряд
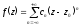 ,
(3.11)
,
(3.11)
коефіцієнти якого обчислюються за формулою
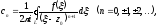 (3.12)
(3.12)
де
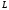 - довільний круг з центром
- довільний круг з центром
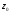 ,
що лежить в середині даного кільця.
,
що лежить в середині даного кільця.
Ряд
(3.11) називається рядом
Лорана
для функції
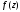 в розглядуваному кільці.
в розглядуваному кільці.
Візьмемо
довільну точку
 всередині кільця
всередині кільця
 і проведемо два кола
і проведемо два кола
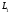 та
та
 з центрами в точці
з центрами в точці
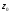 так, щоб точка
так, щоб точка
 була між ними і щоб кожне коло знаходилося
всередині даного кільця (див. рис. 15).
була між ними і щоб кожне коло знаходилося
всередині даного кільця (див. рис. 15).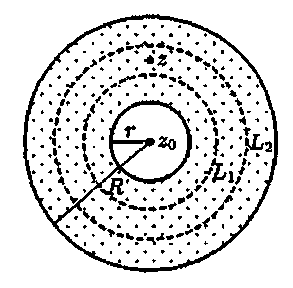
Функція
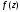 аналітична в кільці між колами
аналітична в кільці між колами
 й
й
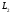 та на самих колах. Тому за формулою Коші
для рис. 15
багатозв’язної області маємо:
та на самих колах. Тому за формулою Коші
для рис. 15
багатозв’язної області маємо:
Рис.
15
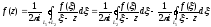 (3.13)
(3.13)
де обидва
кола
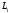 і
і
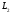 обходяться проти годинникової стрілки.
обходяться проти годинникової стрілки.
Перетворимо доданки, що стоять у правій частині рівності (3.13), міркуючи, як і при виведенні формули Тейлора.
На
колі
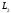 виконується нерівність
виконується нерівність
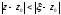 ,
або
,
або
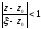 .
Тому дріб
.
Тому дріб
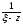 можна подати у вигляді
можна подати у вигляді
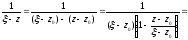

Тоді
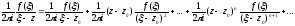
Проінтегруєм
цю рівність по контуру
 :
:
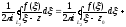
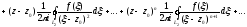 ,
(3.14)
,
(3.14)
тобто
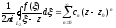 ,
де
,
де

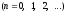
(тут
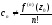 ,
тому що функція
,
тому що функція
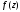 ,
можливо, не аналітична в точці
,
можливо, не аналітична в точці
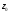 ).
).
На колі
 маємо
маємо
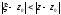 ,
або
,
або
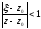 .
Тоді
.
Тоді
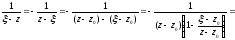
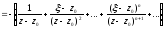 .
.
Виходить,
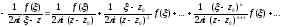
Проінтегруєм цю рівність почленно по контуру L1:
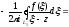

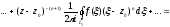
 (3.15)
(3.15)
тобто
 де
де
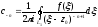 (n
=
1,2,3…)...
(n
=
1,2,3…)...
Поставивши розклад (3.14) та (3.15) у рівність (3.13), отримаємо
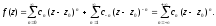
Формули
для коефіцієнтів cn
і c-n
можна об'єднати, взявши замість контуру
L1
і
L2
будь-яке
коло L
з центром у точці z0,
що лежить у кільці між L1
і
L2
(випливає з теореми Коші для багатозв’язної
області):
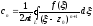 (n=
0,1,
2,…)...
(n=
0,1,
2,…)...
Можна довести, що функція f (z), аналітична в даному кільці
r|z-z0|R, розкладається в ряд Лорана (3.11) єдиним чином.
Ряд Лорана для функції
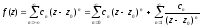
складається з двох частин. Перша частина ряду Лорана, тобто ряд

називається правильною частиною ряду Лорана; цей ряд збіжний до аналітичної функції f1(z) усередині круга |z-z0|<R. Друга частина ряду Лорана, тобто ряд
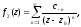
називається
головною
частиною ряду Лорана;
цей ряд збіжний до аналітичної функції
f2(z)
поза кругом
 .
.
Усередині
кільця
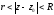 ряд
ряд
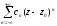 збіжний до аналітичної функції f(z)=f1(z)+
f2(z).
збіжний до аналітичної функції f(z)=f1(z)+
f2(z).
Зокрема,
якщо функція f(z)
не має особливих точок усередині круга
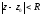 ,
то її розклад в ряд Лорана перетворюється
в ряд Тейлора.
,
то її розклад в ряд Лорана перетворюється
в ряд Тейлора.
Зауваження.
На практиці при розкладанні функції в
ряд Лорана використовують відомі
розклади основних елементарних функцій;
дріб вигляду
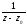 розкладається в ряд, що являє собою
геометричну прогресію; дріб вигляду
розкладається в ряд, що являє собою
геометричну прогресію; дріб вигляду
 ,
де k>1
— ціле, розкладається в ряд, що отримується
з ряду геометричної прогресії послідовним
диференціюванням (k-1)
раз; складний дріб подається у вигляді
суми найпростіших дробів.
,
де k>1
— ціле, розкладається в ряд, що отримується
з ряду геометричної прогресії послідовним
диференціюванням (k-1)
раз; складний дріб подається у вигляді
суми найпростіших дробів.
Приклад
14.
Розкласти в ряд Лорана функцію
 в околі точки z0
= 0.
в околі точки z0
= 0.
○ Скористаємося відомим розкладом
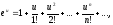
справедливим
на всій комплексній площині. Поклавши
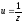 ,
отримаємо
,
отримаємо
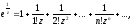 z
0. ●
z
0. ●
Приклад
15.
Розкласти
в ряд Лорана функцію
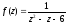
в околі точки z0 = 0.
○ Функція
має дві особливі точки:
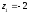 і
і
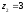 .
Вона аналітична в областях: а)
.
Вона аналітична в областях: а)
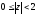 ;
б)
;
б)
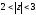 ;
в)
;
в)
 .
.
Подамо
функцію f(z)
у вигляді
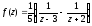 .
.
а) У крузі |z|<2 (рис. 16) маємо:
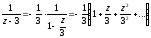
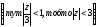 ,
,
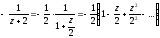
 .
.
Отже,
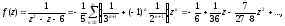
ряд Лорана функції f(z) перетворюється в ряд Тейлора.
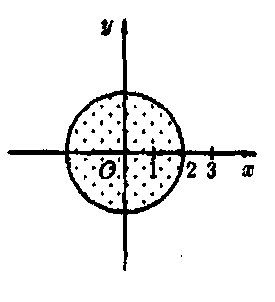
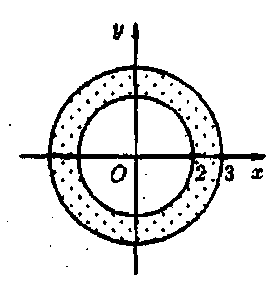
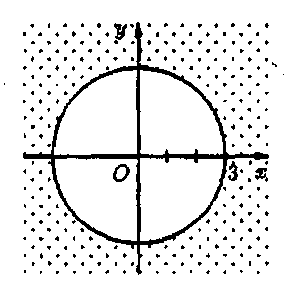
Рис. 16 Рис. 17 Рис. 18
б)
У кільці
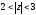 (рис. 17) маємо:
(рис. 17) маємо:
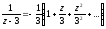 (|z|
< 3),
(|z|
< 3),
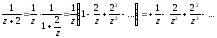 (|z|
> 2).
(|z|
> 2).
Отже,
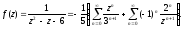
в) В області |z|>3 (рис. 18) маємо:
 (|z|>3),
(|z|>3),
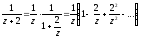 (|z|>2).
(|z|>2).
Отже,
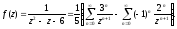 ●
●
